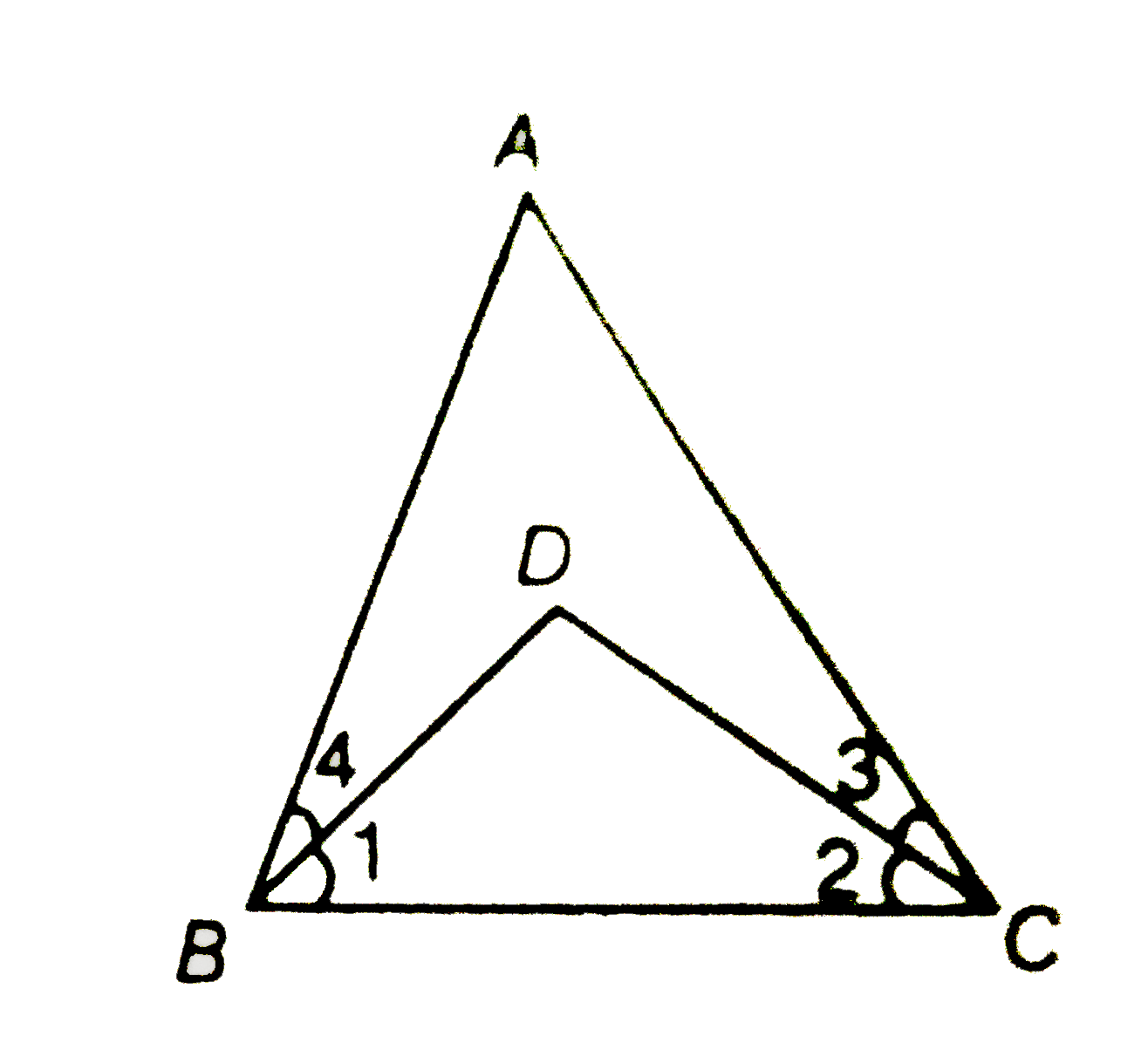
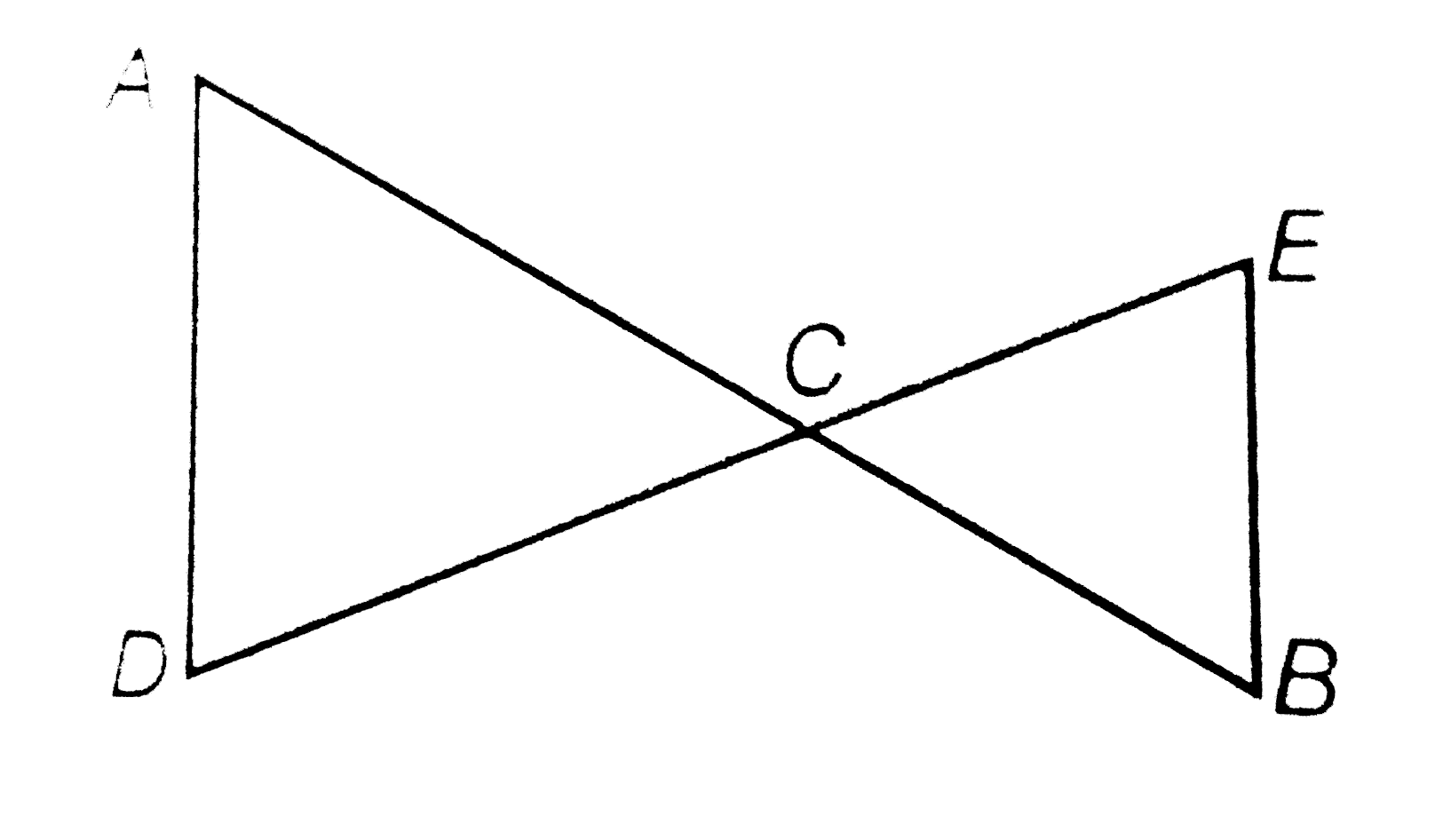
In the ajoining figure , we have∠ABC=∠ACBand∠3=∠4. Show that BD=DC.
Video Solution
Text Solution
Given , ∠ABC=∠ACB ... (i)
and ∠4=∠3 ...(ii)
According to Eulid's axiom , if equals are subtracted from equals, then remainders are also equal. On subtracting Eq. (ii) From Eq.(i) we get
∠ABC−∠4=∠ACB−∠3
⇒∠1=∠2
Now , in ΔBDC,∠1=∠2
⇒ DC =BD [sides opposite to equales are equal]
∴ BD=DC.
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
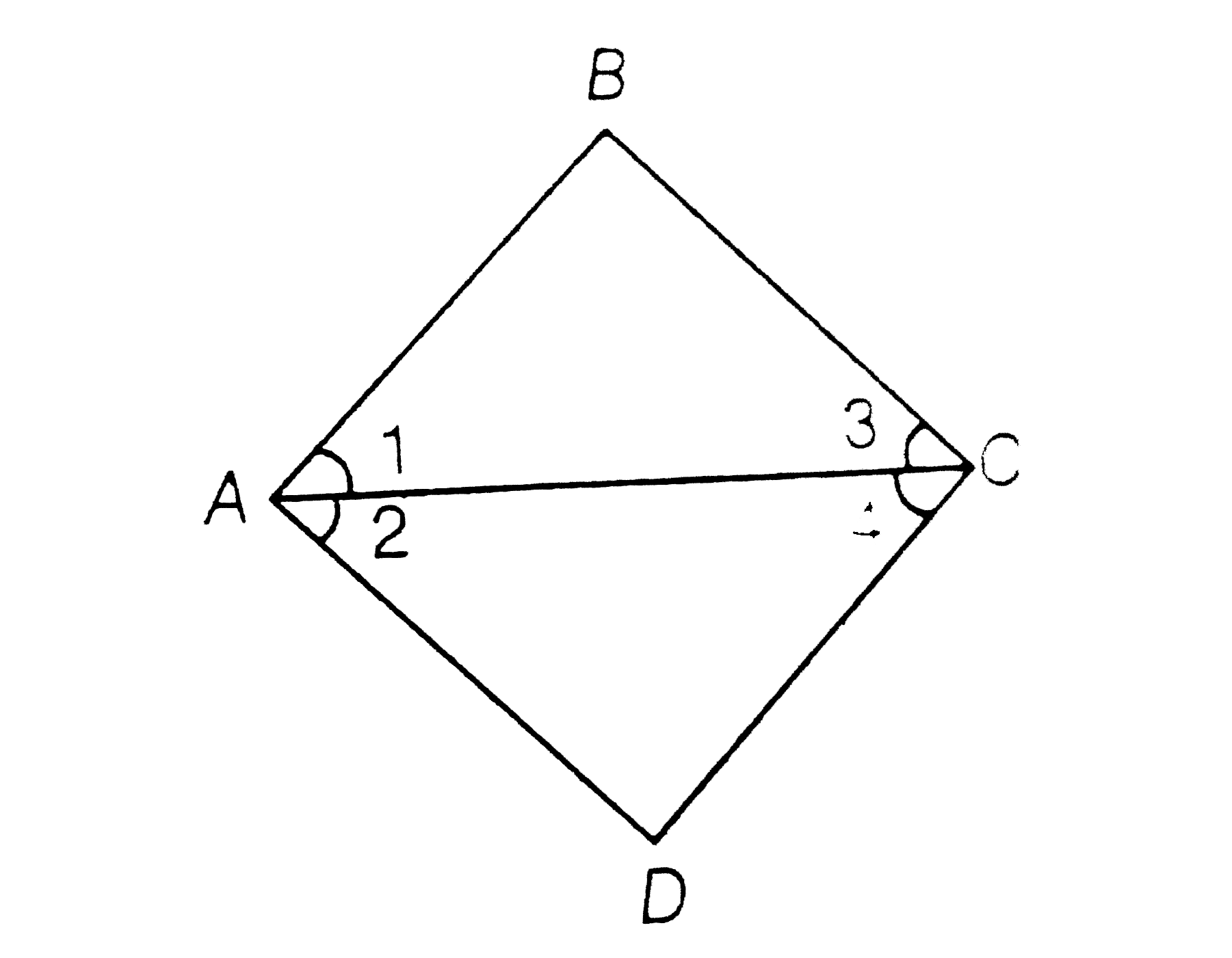
In the adjoining figure, we have ∠1=∠3and∠2=∠4. Show that ∠A=∠C.
 View Solution
View SolutionIn the adjoining figure, we have ∠1=∠2 and ∠2=∠3. Show that ∠1=∠3.
 View Solution
View SolutionIn the given figure we have ∠1=∠3and∠2=∠4 show that ∠A=∠C
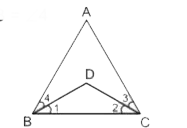
View SolutionIn given figure ∠ABC=∠ACBand∠3=∠4
Show that ∠1=∠2
 View Solution
View SolutionIn the given figure we have ∠1=∠3,∠2=∠4and∠3=∠4 prove that ∠1=∠2
View SolutionIn the adjoining figure ∠BAD=a,∠ABC=band∠BCD=c and ∠ADC=d, find the value of ∠ABC in terms of a, c and d:
 View Solution
View SolutionIn the given figure ∠1=∠3and∠2=∠4
then show that ∠BAD=∠BCD
 View Solution
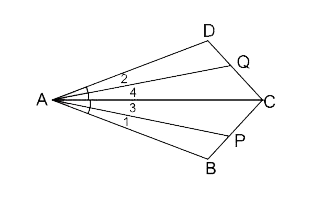
View SolutionIn the given figure , AB=AD , ∠1=∠2and∠3=∠4 .Prove that AP=AQ
 View Solution
View SolutionIn the given figure ∠1=∠2 and ∠2=∠3
then show that ∠1=∠3
 View Solution
View SolutionIn the adjoining figure , we have AC=DC and CB = CE. Show that AB=DE.
 View Solution
View Solution

