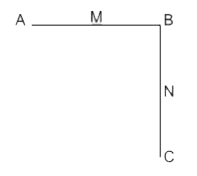
In the adjoining figure
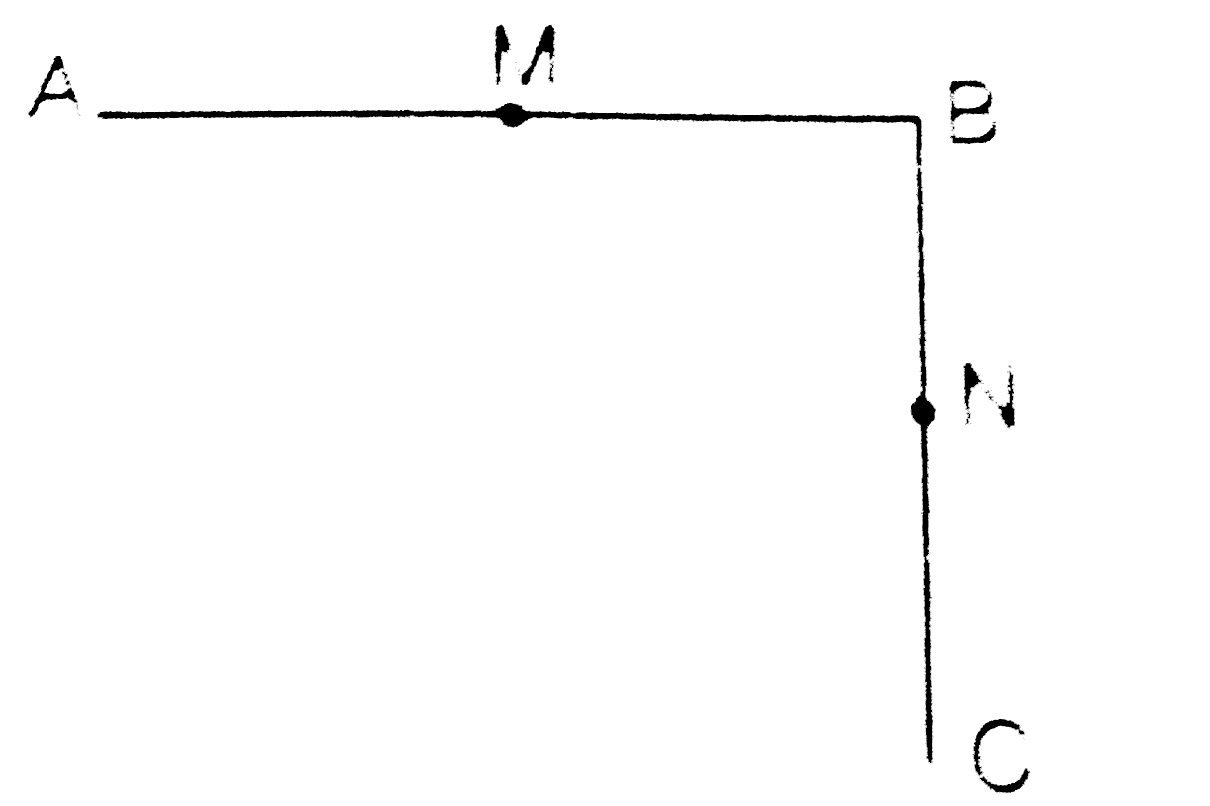
(i) AB=BC, M is the mid -point of AB and N is the mid- point of BC. Show that AM=NC.
(ii) BM=BN,M is the mid- point of AB and N is the mid - point of BC. Show that AB=BC.
Video Solution
Text Solution
Given, AB=BC …(i)
M is the mid - point of AB.
AM=MB=12AB …(ii)
and N is the mid - point of BC.
BN=NC=12BC …(iii)
According to Euclid's axiom , things which are halves of the same things are equal to one another . From Eq. (i) , AB=BC
On multiplying both sides by 12 , we get
12AB=12BC
⇒AM=NC [using Eqs. (ii) and (iii)]
(ii) Given, BM=BN ...(i)
M is the mid -point of AB.
∴AM=BM=12AB
⇒2AM=2BM=AB ...(ii)
and N is the mid - point of BC.
∴BN=NC=12BC
⇒2BN=2NC=BC ...(iii)
According to Euclid's which are double of the same thing are equal to one another.
On multiplying both sides of Eq.(i) by 2, we get
2BM=2BN
⇒AB=BC [using Eqs. (ii) and (iii)]
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
Locus of mid point of AB is
Ax2=−2yB2x2=−yCx2=−4yDx22−y21=−1ABCD is a square. M is the mid-point of AB and N is the mid-point of BC. DM and AN are joined and they meet at O, then which of the following is correct ?
AOA : OM = 1 : 2BAN = MDC∠ADM=∠ANBD∠AMD=∠BAN
in figure , M is the mid-point of AB and N is the mid-point of BC (1) if AB=BC , prove that AM=NC
View SolutionWe have AC=XD , C is the mid point of AB and D is the mid point of XY, Using Euclid's axiom ,show that AB=XY
View SolutionIn the adjoining figure , we have X and Y are the mid - point of AC and BC and AX = CY . Show that AC =BC.
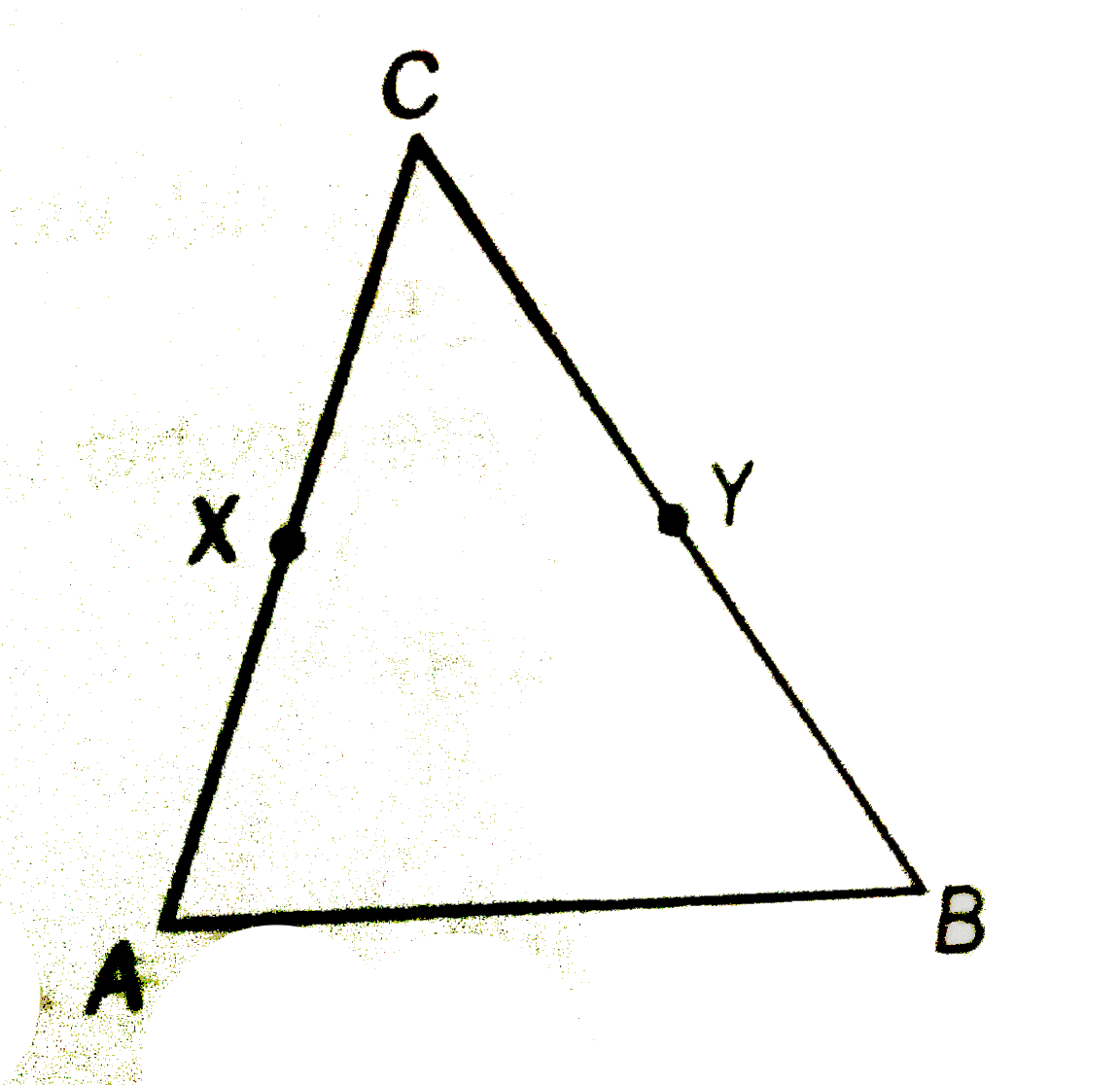
View SolutionPoint M is the mid point of seg AB and AB = 14 unit then AM =?
View SolutionABC is any triangle. P is the mid-point of BC,Q is the mid-point of CAand R is the mid-point of AB. The expression −−→AP+−−→BQ+−−→CR equals
View SolutionIn the given figure, D is the mid-point of BC, E is the mid-point of BD and O is the mid-point of AE. Find the ratio of area of ΔBOEandΔABC

View Solution