In the adjoining figure , we have AC=DC and CB = CE. Show that AB=DE.
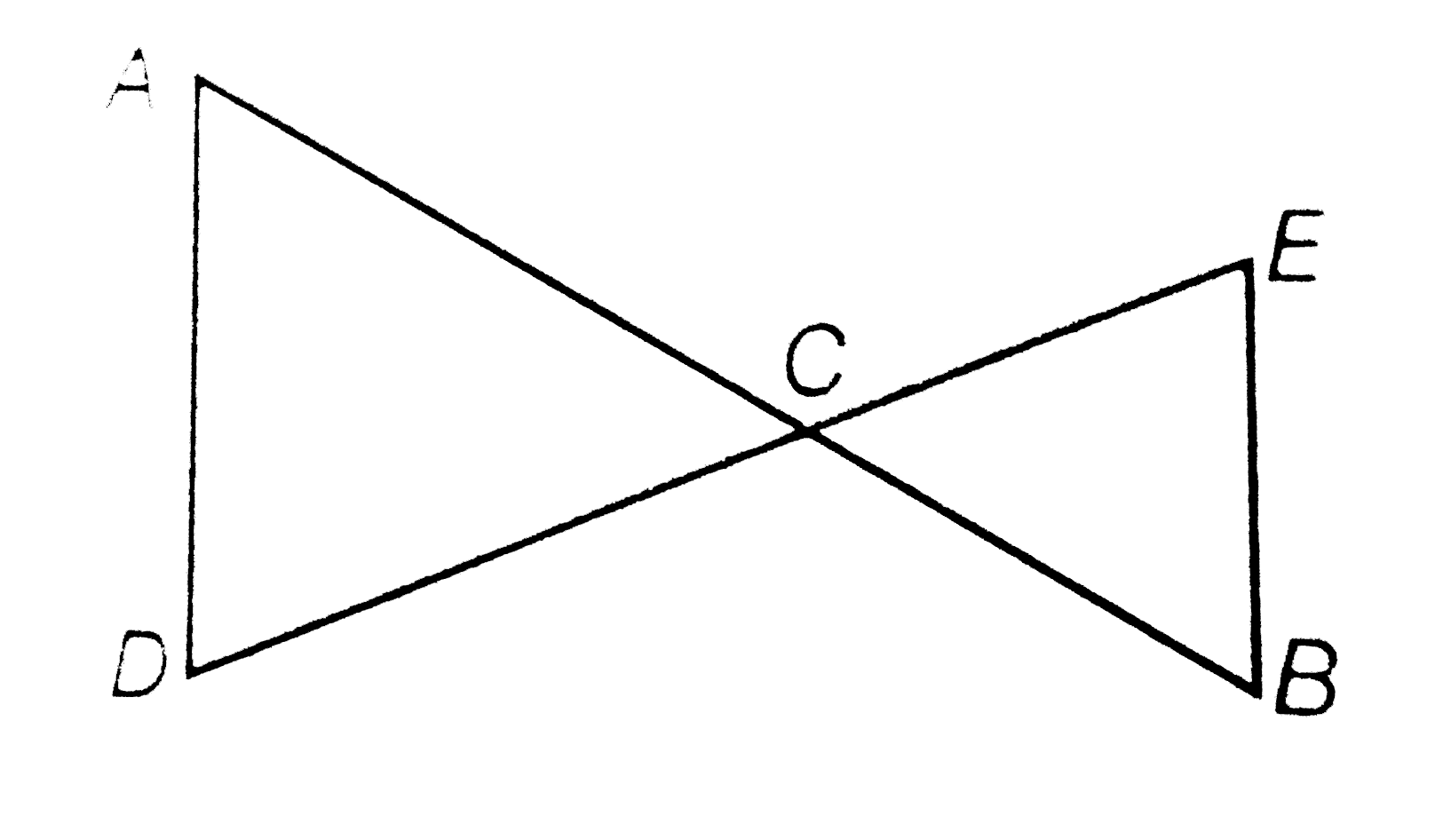
Given, AC=DC …(i)
and CB=CE …(ii)
According to Euclid's axiom , if equals are added to equals , then wholes are also equal. So . On adding Eqs. (i) and (ii), we get
AC+CB=DC+CE
⇒ AB=DE
Topper's Solved these Questions
Similar Questions
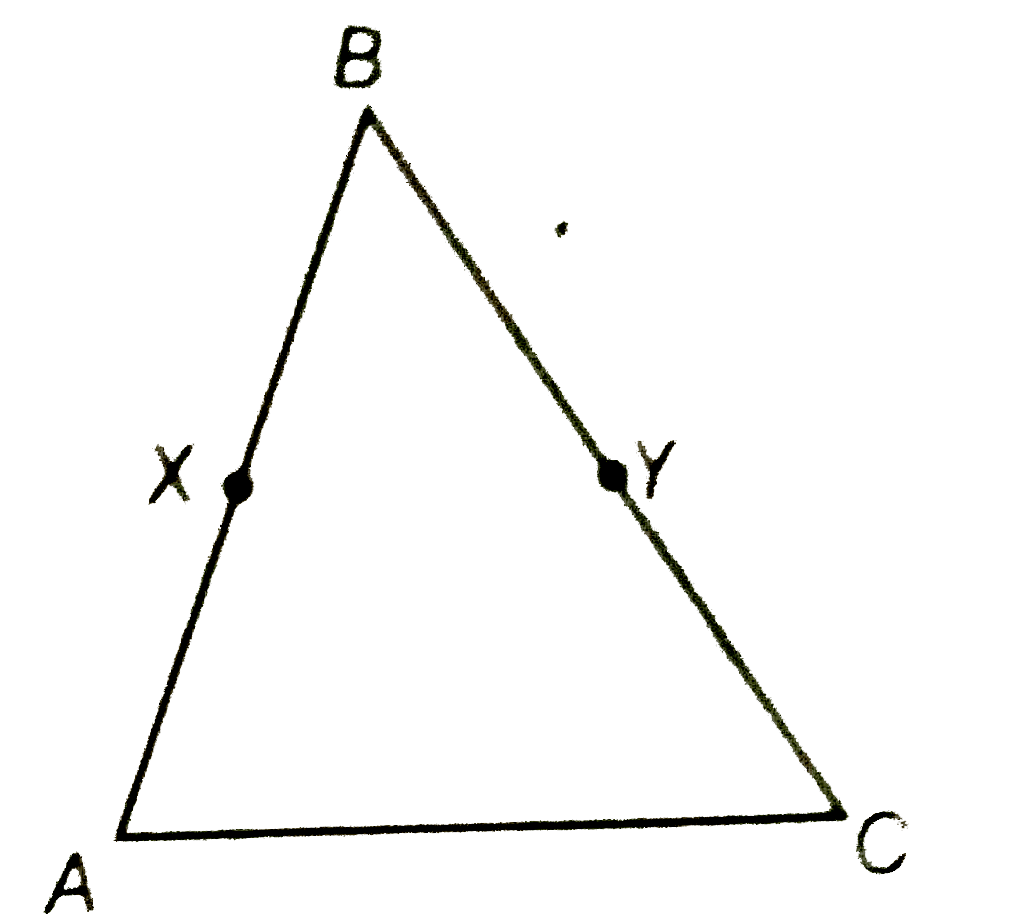
In the adjoining figure, if AB = BC and BX =BY, then show that AX=CY
 View Solution
View SolutionIn the adjoining figure, AB = AC and BD = DC. Prove that △ADB=△ADC and hence show that
(i) ∠ADB=∠ADC=90∘, (ii) ∠BAD=∠CAD.
 View Solution
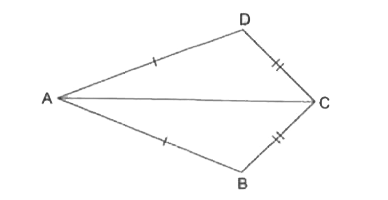
View SolutionIn the adjoining figure,
AB = AD and CB = CD.
Is △ABC≅△ADC ?,
 View Solution
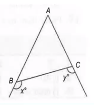
View SolutionIn the adjoining figure, x>y, Prove that AB>AC
 View Solution
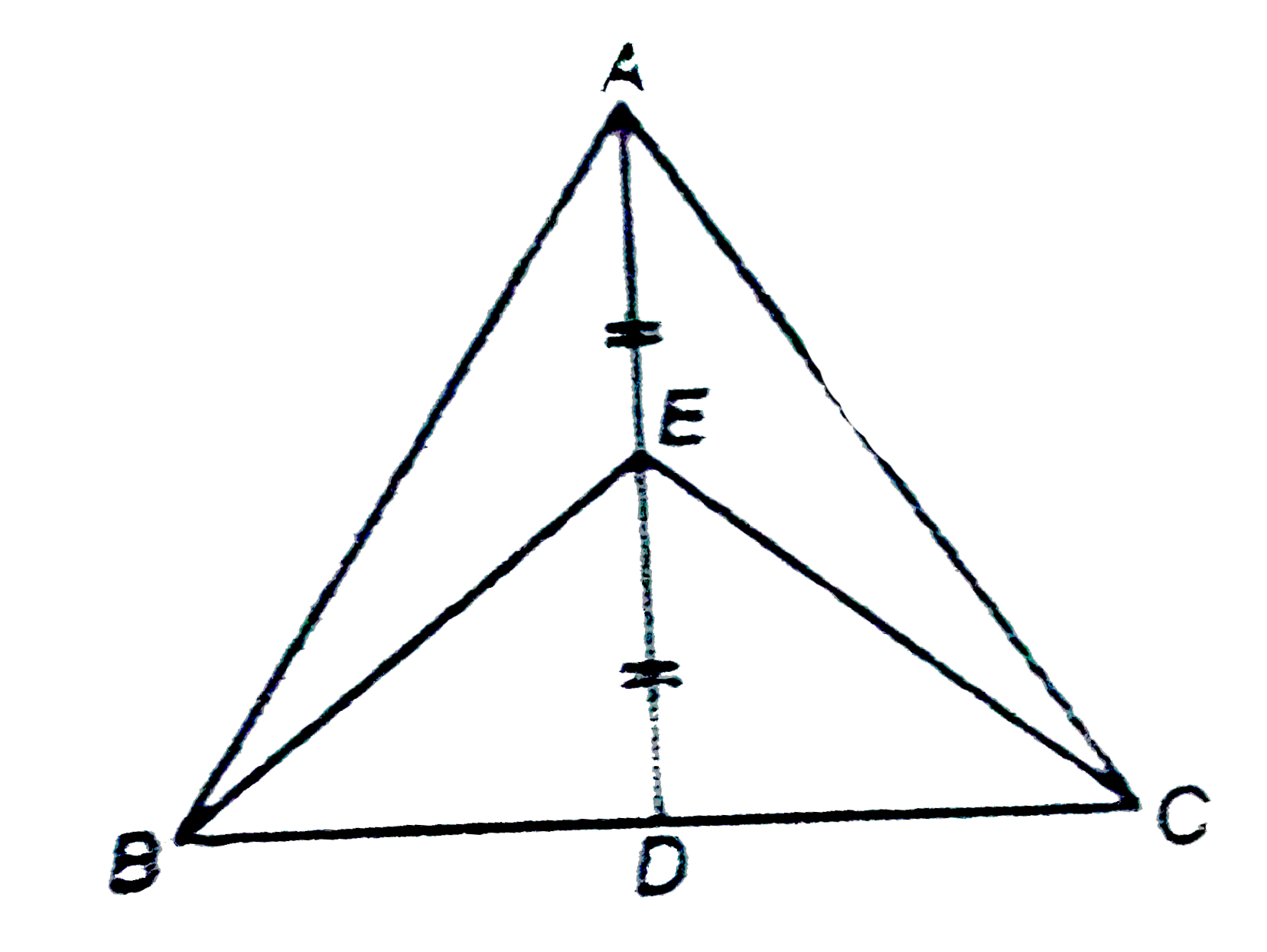
View SolutionIn the adjoining figure, BD = DC and AE = ED. Prove that
area of ΔACE=14 area of ΔABC
 View Solution
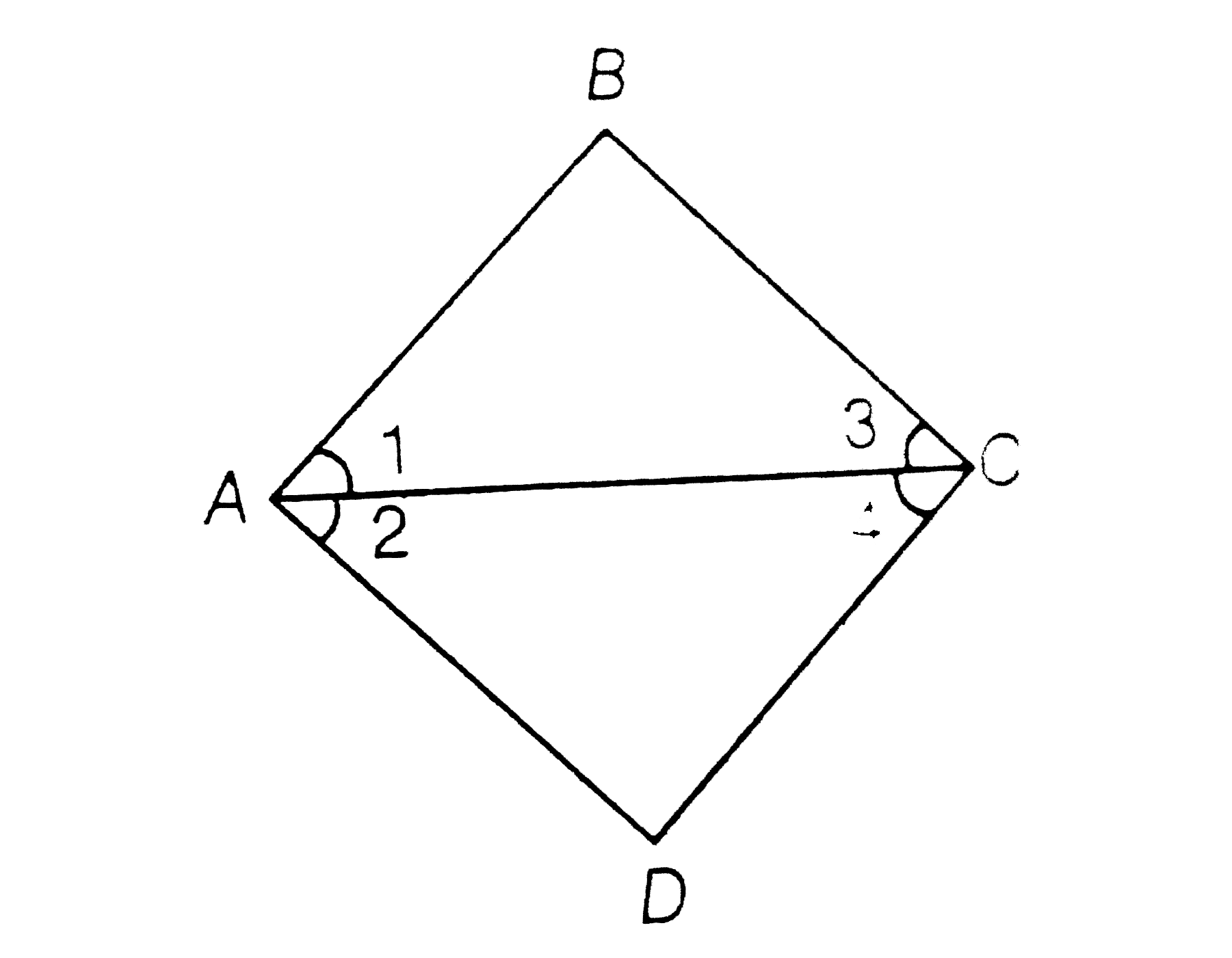
View SolutionIn the adjoining figure, we have ∠1=∠3and∠2=∠4. Show that ∠A=∠C.
 View Solution
View SolutionIn the adjoining figure,AB=AC and BD=DC Prove that ΔADB≡ΔADC and hence show that (i) ∠ADB≡∠ADC=90∘ , (ii) ∠BAD=∠CAD
View SolutionIn the adjoining figure,AB=AC.Find the value of x
View SolutionIn the adjoining figure, find AC . (FIGURE)
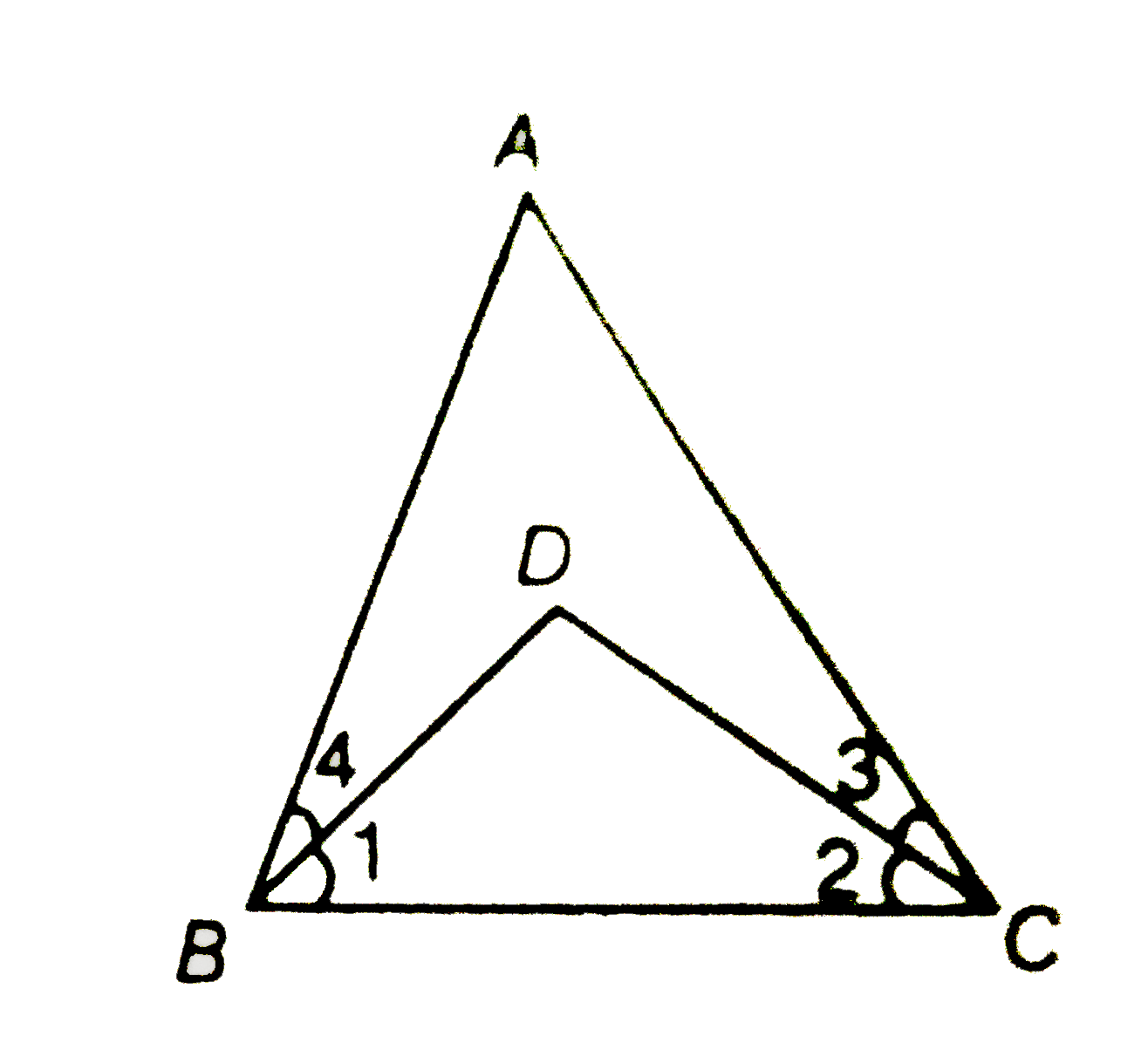
View SolutionIn the ajoining figure , we have∠ABC=∠ACBand∠3=∠4. Show that BD=DC.
 View Solution
View Solution

