The mid-point of the sides of triangle along with any of the vertices as the fourth point make a parallelogram of area equal to
12ar(ABC)
13ar(ABC)
2ar(ABC)
ar(ABC)
The correct Answer is:A
Step by step video, text & image solution for The mid-point of the sides of triangle along with any of the vertices as the fourth point make a parallelogram of area equal to by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
Similar Questions
The mid points of the sides of a triangle ABC along with any of the vertices as the fourth point make a parallelogram of area equal to:
(a)ar (ABC) (b) 12ar (ABC) 13ar (ABC) (d) 14 ar (ABC)View SolutionIf the mid-points of the sides of a quadrilateral are joined in order, prove that the area of the parallelogram, so formed will be half of the area of the given quadrilateral (figure).
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The mid-point of the sides of triangle along with any of the vertices as the fourth point make a parallelogram of area equal to
A12ar(△ABC)B13ar(△ABC)C14ar(△ABC)Dar(△ABC) - Question 2 - Select One
The midpoints of the sides of a triangle along with any of the vertices as the fourth point makes a parallelogram of area equal to
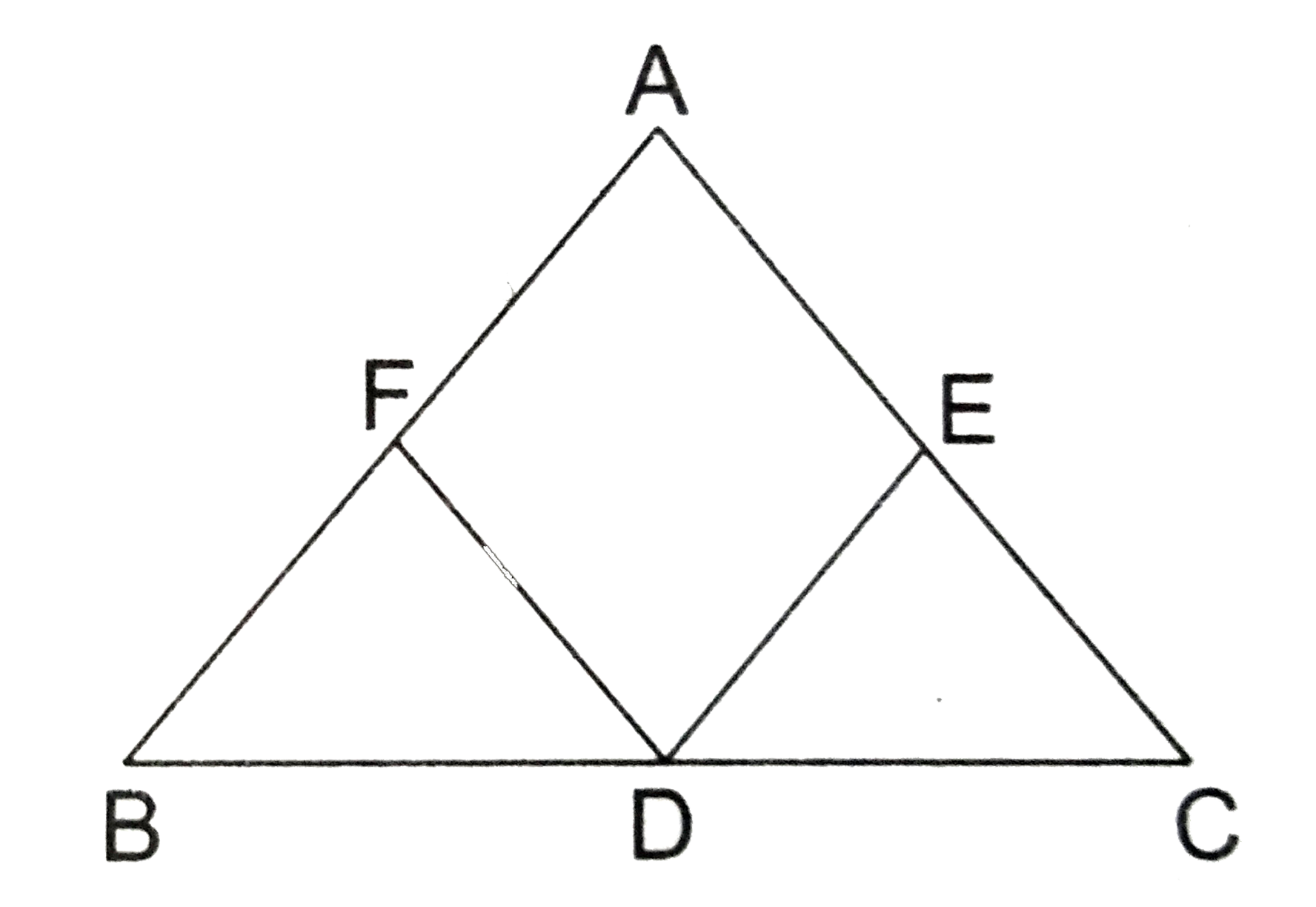 A2(ar△ABC)B13(ar△ABC)C14(ar△ABC)Dar(△ABC)
A2(ar△ABC)B13(ar△ABC)C14(ar△ABC)Dar(△ABC) - Question 3 - Select One
The triangle is formed by joining the mid-points of the sides AB,BC and CA of △ABCand the area of △PQR is 6cm2, then the area of △ABC is :
A36cm2B12cm2C18cm2D24cm2
Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0,−1),(2,1)and(0,3). Find the ratio of this area to the area of the given triangle.
View SolutionOne side of an equilateral triangle is 36 cm. The mid-points of its sides are joined to form another triangle. Again another triangle is formed by joining the mid-points of the sides of this triangle and the process is continued indefinitely. Determine the sum of areas of all such triangles including the given triangle.
View SolutionD, E and F are the mid-points of the sides BC, CA and AB of a triangle ABC. Show that
BDEF is a parallelogramView SolutionIn an equilateral triangle another equilateral triangle is drawn inside joining the mid-points of the sides of given equilateral triangle and the process is continued up to 7 times. What is the ratio of area of fourth triangle to that of seventh triangle ?
View SolutionThe mid-points of the sides of a triangle are (1,5,−1),(0,4,−2)and(2,3,4). Find its vertices.
View Solution

