O is any point on the diagonal PR of a parallelogram PQRS (figure). Prove that ar(ΔPSO)=ar(ΔPQO).

Video Solution
Text Solution
Given In a parallelogram PQRS, O is any point on the diagonal PR.
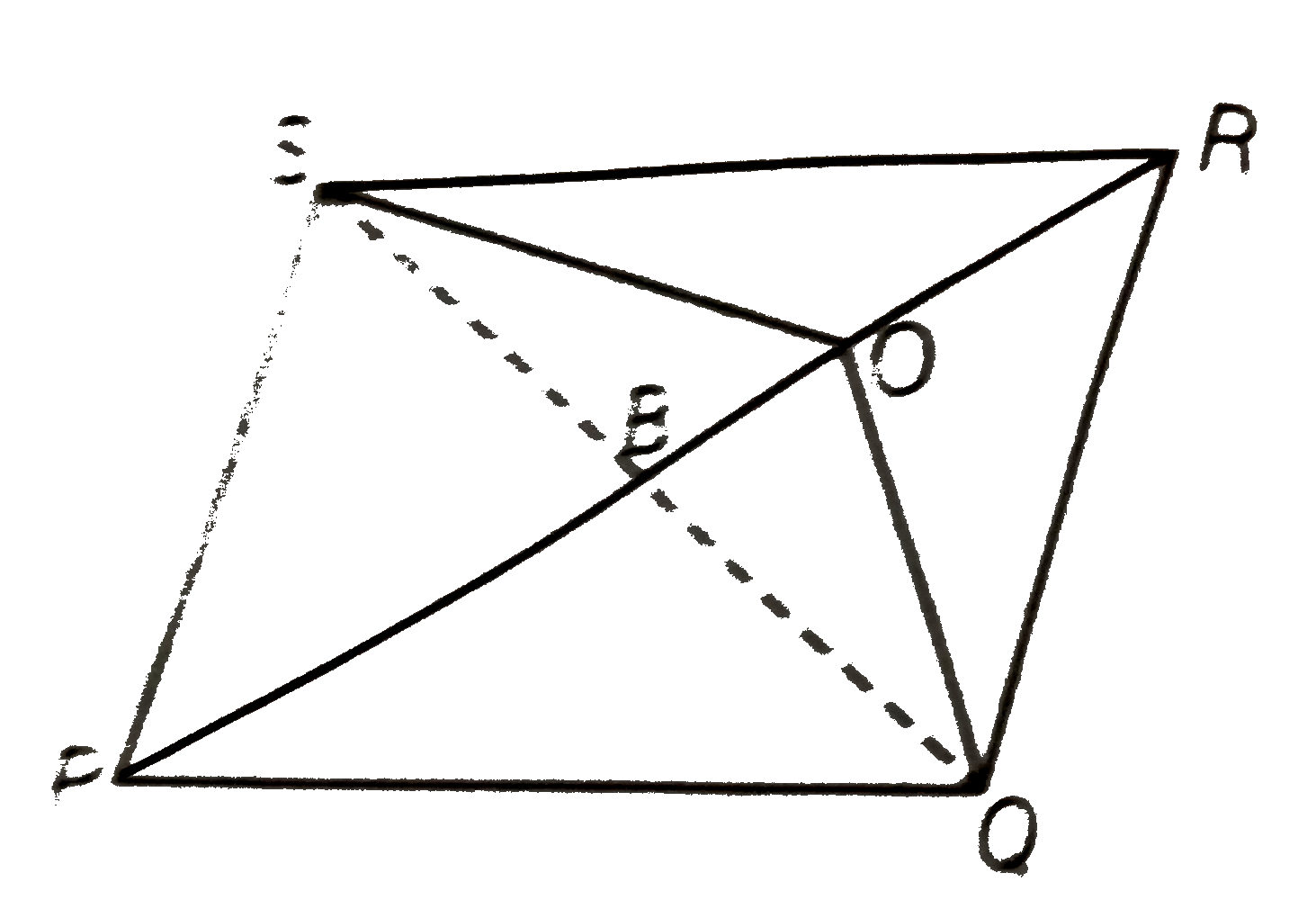
To prove ar(ΔPSO)=ar(ΔPQO)
Construction Join SQ which intersects PR at B.
Proof We know that, diagonals of a parallelogram bisect each other, so B is the mid-point of SQ.
Here, PB is a median of ΔQPS and we know that, a median of a triangle divides it into two triangles of equal area.
∴ ar(ΔBPQ)=ar(ΔBPS) ...(i)
Also, OB is the median of ΔOSQ.
∴ ar(ΔOBQ)=ar(ΔOBS) ...(ii)
On adding Eqs. (i) and (ii), we get
ar(ΔBPQ)+ar(ΔOBQ)=ar(ΔBPS)+ar(ΔOBS)
⇒ ar(ΔPQO)=ar(ΔPSO) Hence proved.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
Diagonals of a parallelogram PQRS must be a
ArectangleBsquareCcyclic quadrilateralDrhombusAY and BZ are the diagonals of a parallelogram ABYZ, intersecting at O.ar(ΔBYZ) = ?
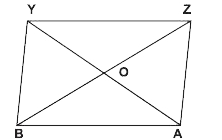 Agreater than ar(ΔABZ)Bis equal to ar(ΔBOA+ΔBOY)Cmore than ar(ΔBOA+ΔBOY)Dless than ar(ΔBOA+ΔBOY)
Agreater than ar(ΔABZ)Bis equal to ar(ΔBOA+ΔBOY)Cmore than ar(ΔBOA+ΔBOY)Dless than ar(ΔBOA+ΔBOY)
O' is any point on diagonal AC of a parallelogram ABCD. Prove that :
area of ΔAOD= area of ΔAOB
View SolutionO is any point on the diagonal BD of the parallelogram ABCD. Prove that ar(OAB)=ar(OBC)
View SolutionIn figure, ABCD and AEFD are two parallelograms. Prove that ar(ΔPEA)=ar(ΔQFD).
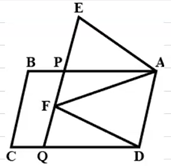
View SolutionIn figure, ABCD and AEFD are two parallelograms. Prove that ar(ΔPEA)=ar(ΔQFD).
View SolutionIn the adjoining figure, P is the point in the interior of a parallelogram ABCD.Show that ar(DeltaAPB) ar(DeltaPCD) =1/2ar(||gm ABCD)
View SolutionIn the given figure, AP||BQ||CR. Prove that ar(ΔAQC)=ar(ΔPBR)

View Solution
