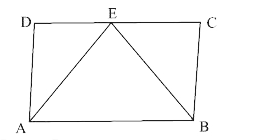
The area of the parallelogram ABCD is 90CM2. Find
(i) ar (ABEF) (ii) ar (ΔABD)
(iii) ar (ΔBEF)
Given, area of parallelogram, ABCD=90cm2.
(i) We know that, parallelograms on the same base and between the same parallel are equal in areas.
Here, parallelograms ABCD and ABEF are on same base AB and between the same parallels AB and CF.
So, ar(ABEF)=ar(ABCD)=90cm2
(ii) We know that, if a triangle and a parallelogram are on the same base and between the same parallels, then area of triangle is equal to half of the area of the parallelogram.
Here, ΔABD and parallelogram ABCD are on the same base AB and between the same parallels AB and CD.
So, ar(ΔABD)=12ar(ABCD)
=12×90=45cm2 [∵ar(ABCD)=90cm2]
(iii) Here, ΔBEF and parallelogram ABEF are on the same base EF and between the same parallels AB and EF.
So, ar(ΔBEF)=12ar(ABEF)
=12×90=45cm2 [∵ar(ABEF)=90cm2. from part (i)]
Topper's Solved these Questions
Similar Questions
Knowledge Check
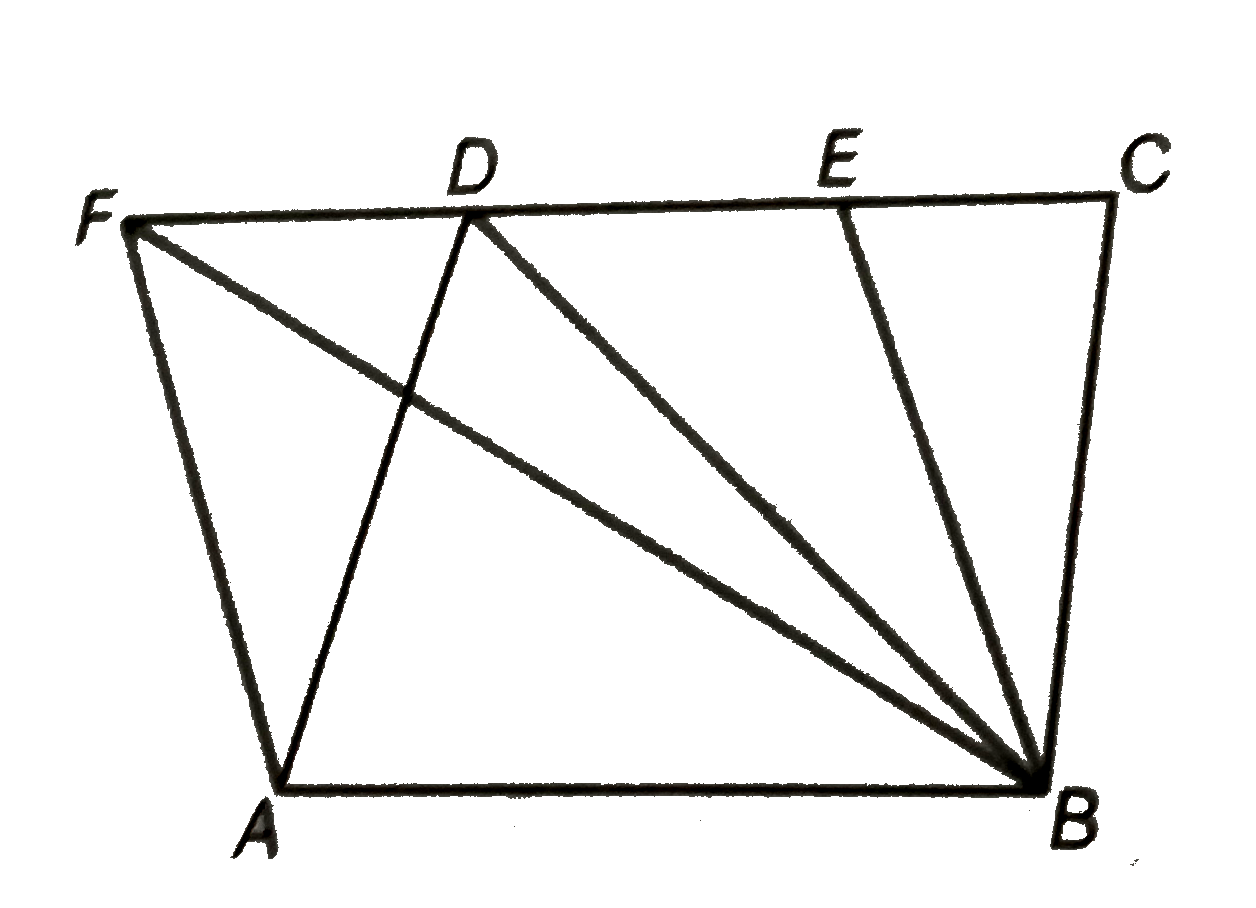
In the figure, ABCD and EFGD are two parallelograms and G is the mid-point of CD. Then, ar(ΔDPC)=ar(EFGD).
 ATrueBFalseCPartially trueDNone of these
ATrueBFalseCPartially trueDNone of theseStatement - 1 Let ABCD and BEFG are two parallelograms such that E lies on AD and C lies on FG then ar(ABCD)ar(BEFG)=1
Statement - 2, ar(ABCD) =12ar(ΔBEC) = ar (BEFG)AStatement - 1 is True, statement -2 is true, statement-2 is a correct explanation fro statement - 1BStatement - 1 is True. Statement - 2 is true statement -2 is Not a correct explanation for statement -1CStatement -1 is True, statement -2 is FalseDStatement -1 is False, Statement -2 is True
In the figure, ABC and BDE are two equilateral triangle such that D is the mid-point of BC. If AE intersects BC at F, show that:
(i) ar(ΔBDE)=14ar(ΔABC) (ii) ar(ΔBDE)=12ar(ΔBAE)
(iii) ar(ΔABC)=2ar(ΔBEC) (iv) ar(ΔBFE)=ar(ΔAFD)
(v) ar(ΔBFE)=2ar(ΔFED) (vi) ar(ΔFED)=18ar(ΔAFC)

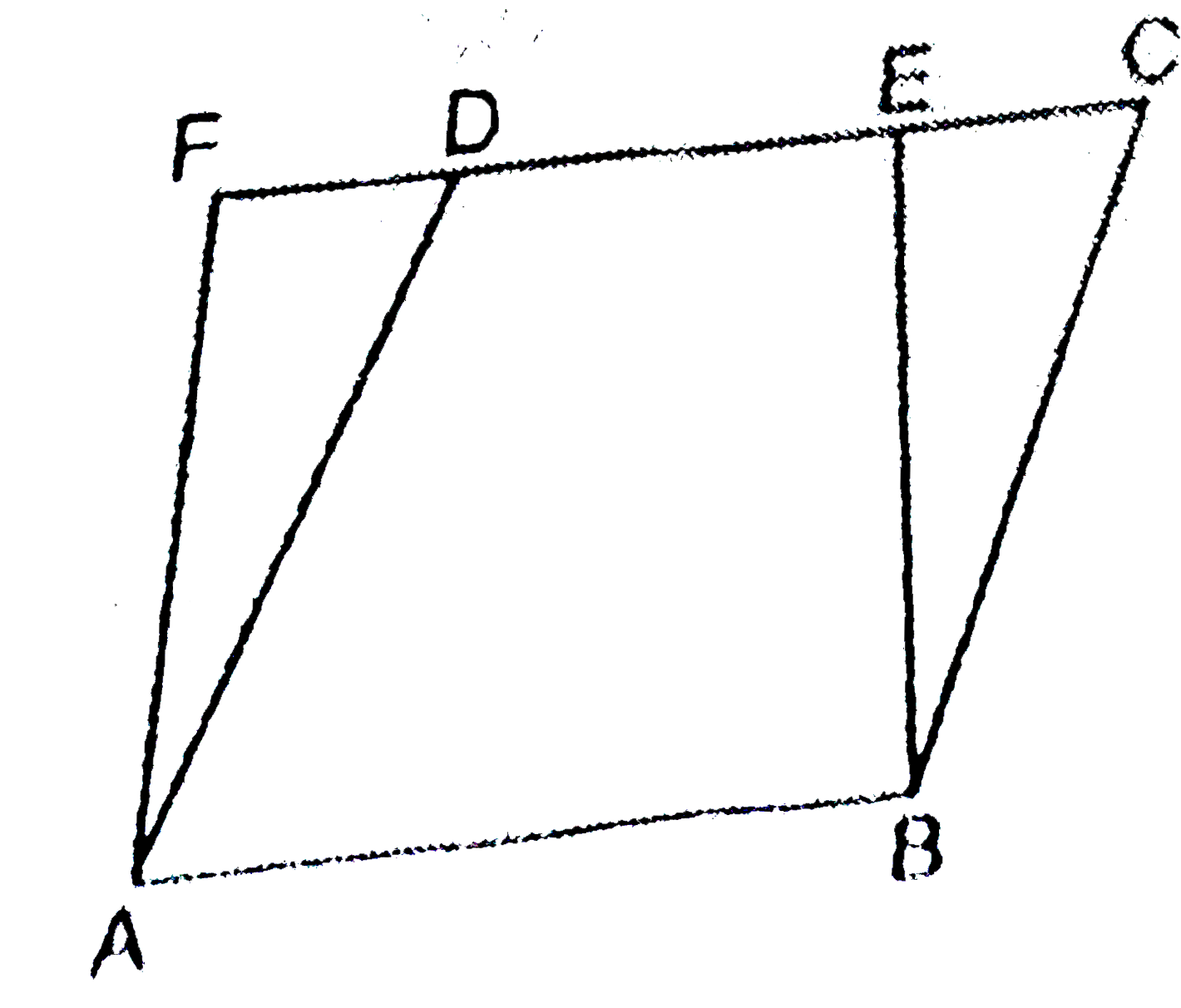
View SolutionIn the given figure, if the area of parallelogram ABCD is 40cm2, find the area of parallelogram ABEF
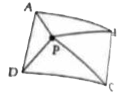
View SolutionIn the adjacent figure P is a point inside the parallelogram ABCD. Prove that
ar (APB) + ar (PCD) = 12 ar (ABCD)
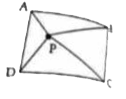
View SolutionIn the adjacent figure P is a point inside the parallelogram ABCD. Prove that
ar (APD) + ar (PBC) = ar (APB) + ar (PCD)
View SolutionIn the figure, P is a point in the interior of a parallelogram ABCD. Show that
(i) ar(△APB)+ar(△PCD=12ar(ABCD)
(ii) ar(△APD)+ar(△PBC)=ar(△APB)+ar(△PCD)

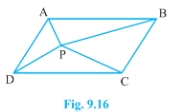
View SolutionIn Fig. 9.16, P is a point in the interior of a parallelogram ABCD. Show that(i) ar(APB)+ar(PCD)=12ar(ABCD)(ii) ar(APD)+ar(PBC)=ar(APB)+ar(PCD)
View Solution