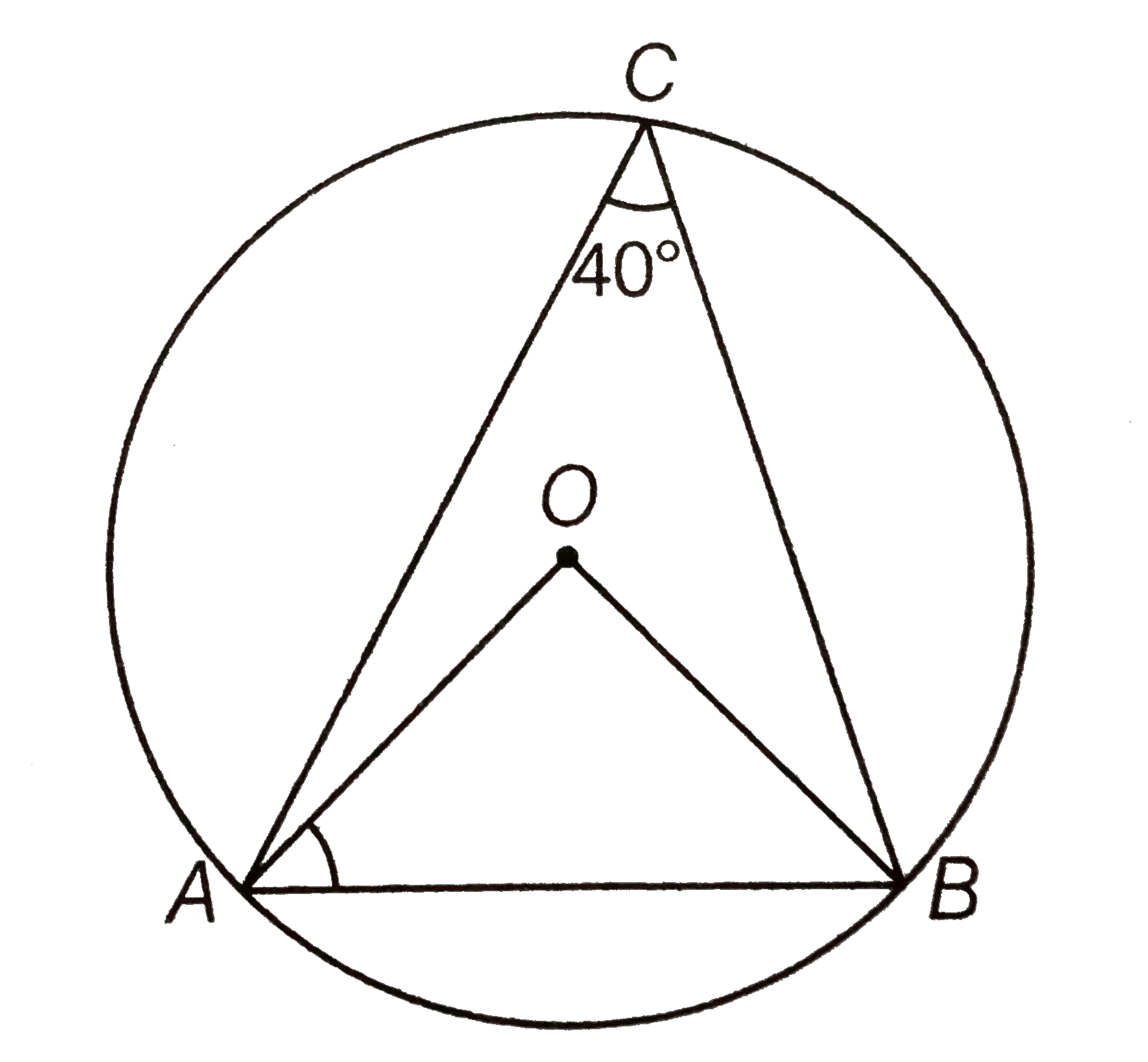
In figure, if ∠OAB=40∘,then∠ACB is equal to
A
50∘
B
40∘
C
60∘
D
70∘
Video Solution
Text Solution
The correct Answer is:A
In ΔOAB,OA=OB[both are the radius of a circle]
∴∠OAB=∠OBA⇒∠OBA=40∘
[angle opposite to equal sides are equal]
Also, ∠AOB+∠OBA+∠BAO=180∘
[by angle sum property of a triangle]
∴∠AOB+40∘+40∘=180∘
⇒∠AOB=180∘−80∘=100∘
We know that, in a circle, the angle subtended by an arc at the centre is twice the angle subtended by it at the remaining part of the circle.
∴∠AOB=2∠ACB
⇒100∘=2∠ACB
∴∠ACB=100∘2=50∘
|
Topper's Solved these Questions
- CIRCLESBook:NCERT EXEMPLARChapter:CIRCLESExercise:Exercise 10.4
Explore 2 Videos
- Areas of Parallelograms and TrianglesBook:NCERT EXEMPLARChapter:Areas of Parallelograms and TrianglesExercise:Areas Of Parallelograms And Triangles
Explore 34 Videos
- CONSTRUCTIONSBook:NCERT EXEMPLARChapter:CONSTRUCTIONSExercise:Long Answer Type Questions
Explore 5 Videos
Similar Questions
Knowledge Check
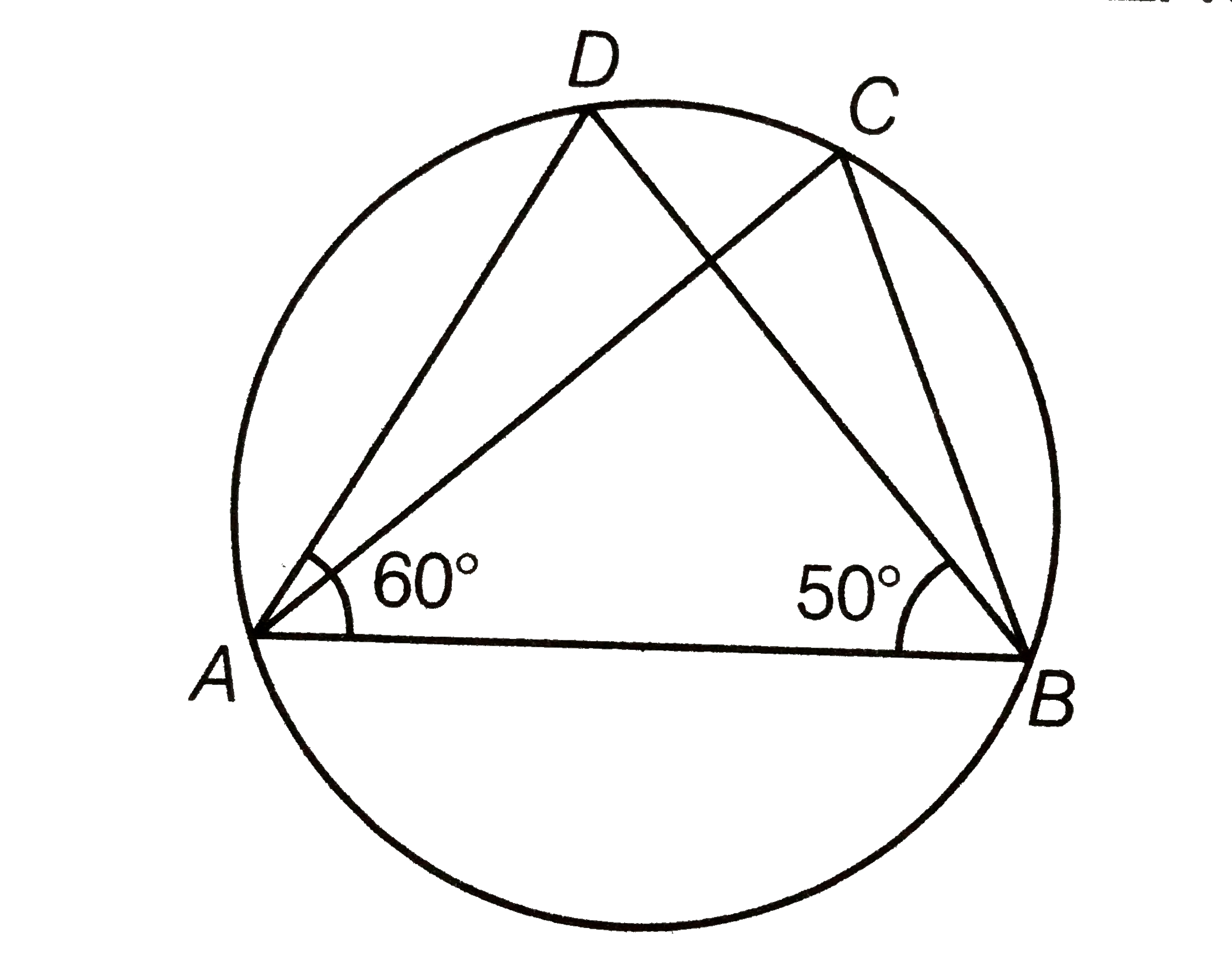
In figure, if ∠DAB=60∘,∠ABD=50∘,then ∠ACB is equal to
 A60∘B50∘C70∘D80∘
A60∘B50∘C70∘D80∘PA and PB are tangents to a circle with centre 0, from a point P outside the circle, and A and B are point on the circle. If ∠APB=30∘, then ∠OAB is equal to:
A25∘B40∘C15∘D50∘PA and PB are two tangents to a circle with centre 0. from a point P outside the circle. A and B are points on the circle. If ∠APB=70∘ then ∠OAB is equal to:
A50∘B35∘C20∘D25∘
In the given figure, ∠OAB=110∘ and ∠BCD=130∘ then ∠ABC is equal to
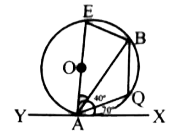
View SolutionIn the figure XY is a tangent to the circle with centre O at A. If ∠BAX=70∘,∠BAQ=40∘ then ∠ABQ is equal to :
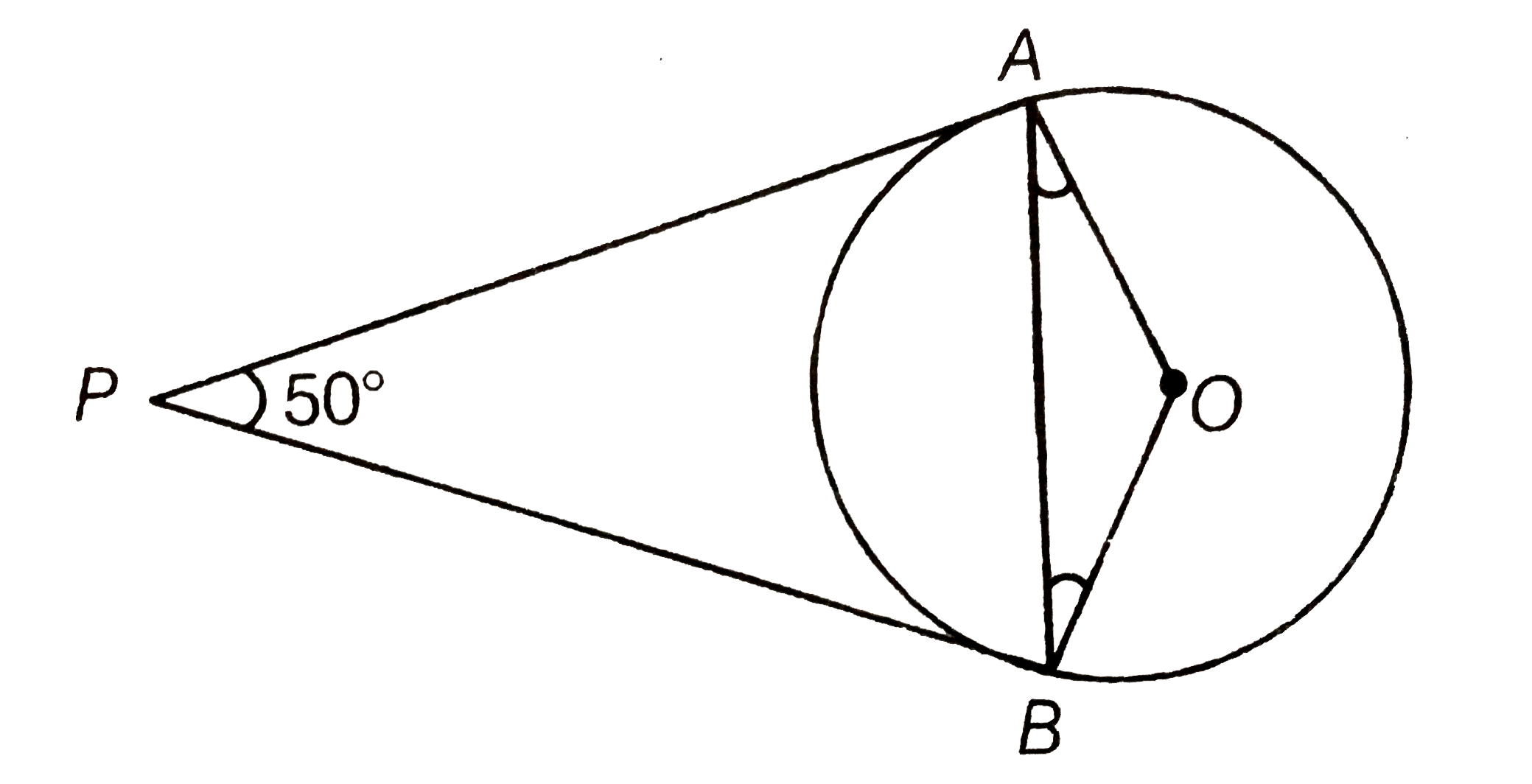
View SolutionIn figure, if PA and PB are tangents to the circle with centre O such that ∠APB=50∘, then ∠OAB is equal to
View SolutionIn the given figure, ABCD is a rectangle whose diagonals AC and BD intersect at 0. If ∠OAB=28∘, then ∠OBC is equal to

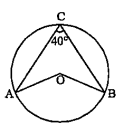
View SolutionIn the given figure O is the centre and ΔACB=40∘ then ∠AOB is equal to
View Solution