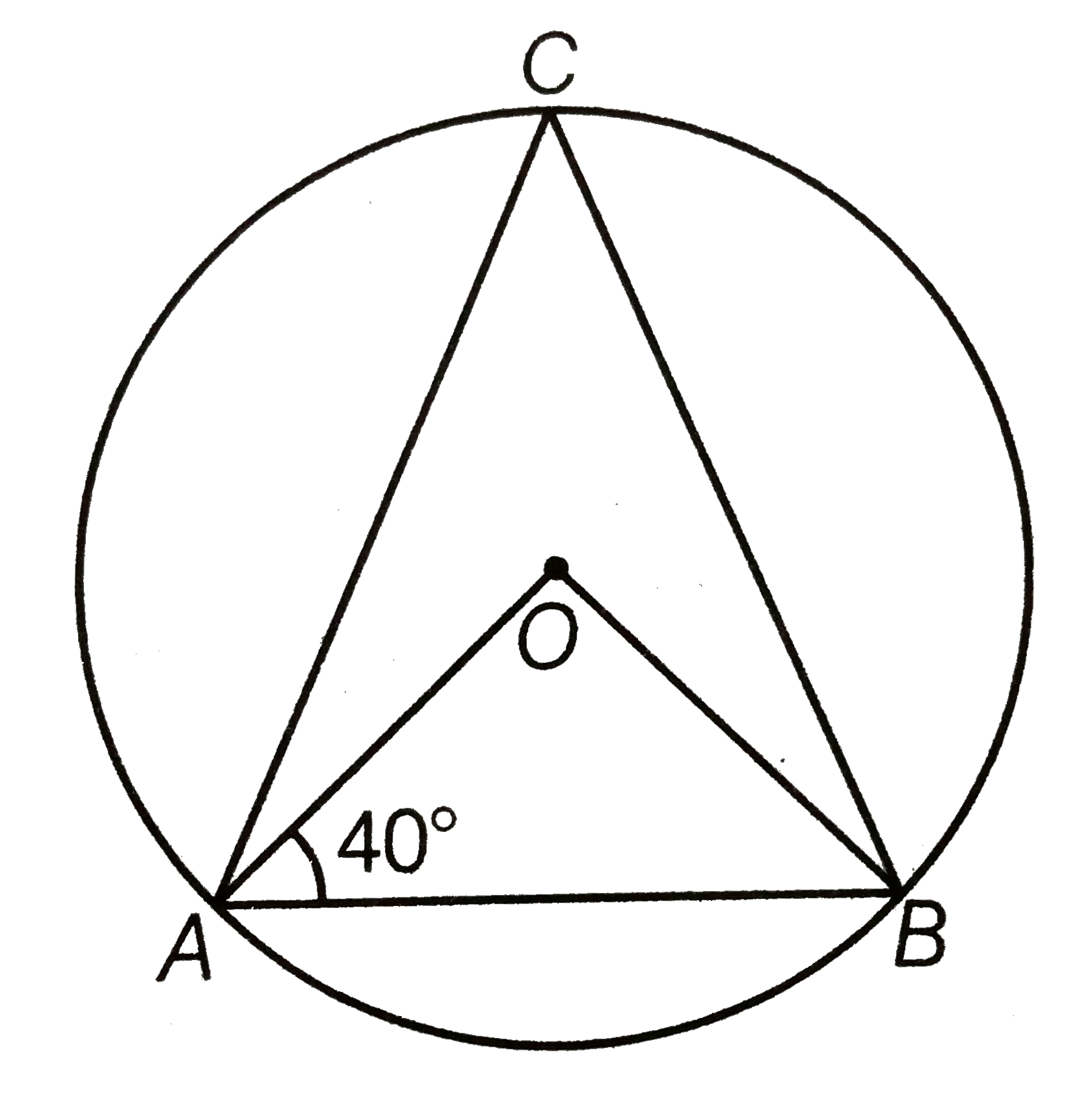
In figure, ∠ACB=40∘. Find ∠OAB.

Video Solution
Text Solution
Given, ∠ACB=40∘
We know that, a segment subtends an angle to the circle is half the angle subtends to the centre.
∴∠AOB=2∠ACB
⇒∠ACB=∠AOB2
⇒40∘=12∠AOB
⇒∠AOB=80∘ ….(i)
In ΔAOB,AO=BO [both are the radius of a circle]
⇒∠OBA=∠OAB ....(ii)
[angles opposite to the equal sides are equal]
We know that, the sum of all three angles in a triangle AOB is 180∘.
∴∠AOB+∠OBA+∠OAB=180∘
⇒80∘+∠OAB+∠OAB=180∘ [form Eqs. (i) and (ii)]
⇒2∠OAB=180∘−80∘
⇒2∠OAB=100∘
∴∠OAB=100∘2=50∘
|
Topper's Solved these Questions
- CIRCLESBOOK - NCERT EXEMPLARCHAPTER - CIRCLESEXERCISE - Exercise 10.4
2 Videos
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLARCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Areas Of Parallelograms And Triangles
34 Videos
- CONSTRUCTIONSBOOK - NCERT EXEMPLARCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions
5 Videos
Similar Questions
Knowledge Check
In figure, if ∠OAB=40∘,then∠ACB is equal to
 A50∘B40∘C60∘D70∘
A50∘B40∘C60∘D70∘In the given figure, ∠CAB=40∘and∠AKB=105∘. Find ∠KCD :
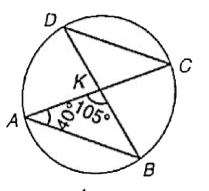 A65∘B35∘C40∘D72∘
A65∘B35∘C40∘D72∘In the given figure, O is the centre of the circle and ∠ACB=25∘ Find ∠AOB
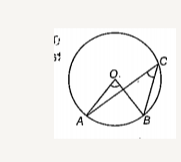 A25∘B50∘C75∘D60∘
A25∘B50∘C75∘D60∘

In the figure (not to scale ), O is the centre of the circle and ∠OBA=30∘. Find ∠ACB
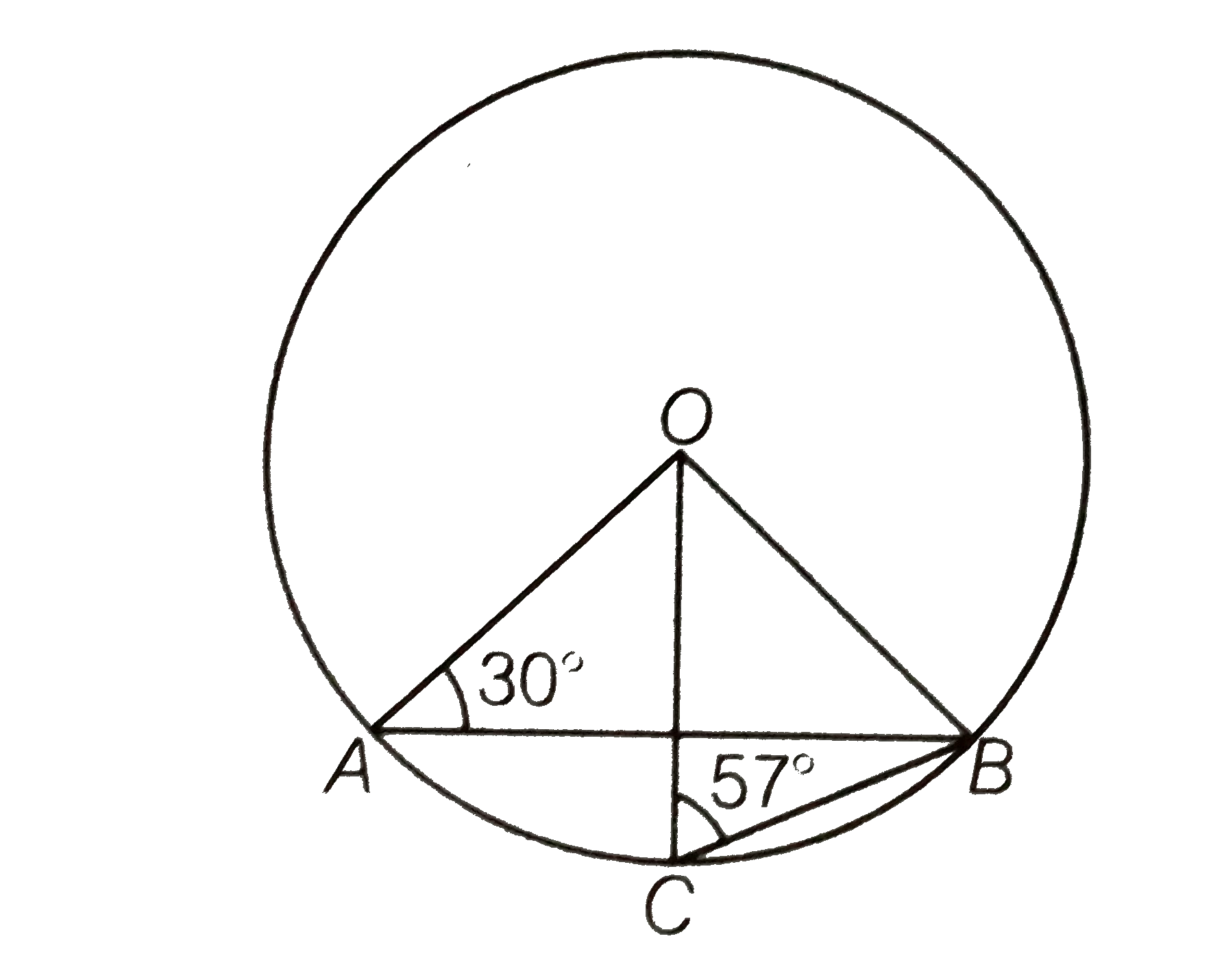
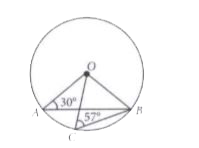
View SolutionIn the given figure, ∠OAB=30∘ and ∠OCB=57∘
Find ∠BOC
View Solution
In the given figure, ∠ACB=60∘,∠CAB=50∘andBC=BD. Find ∠BDC.
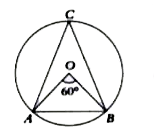
View SolutionIn the following figure , if ∠AOB=60∘ , then ∠ACB=30∘ .
View SolutionIn the adjoining figure , O is the centre of the circle and ∠OAB=60∘. Find ∠APC.

View Solution