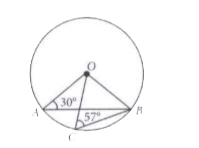
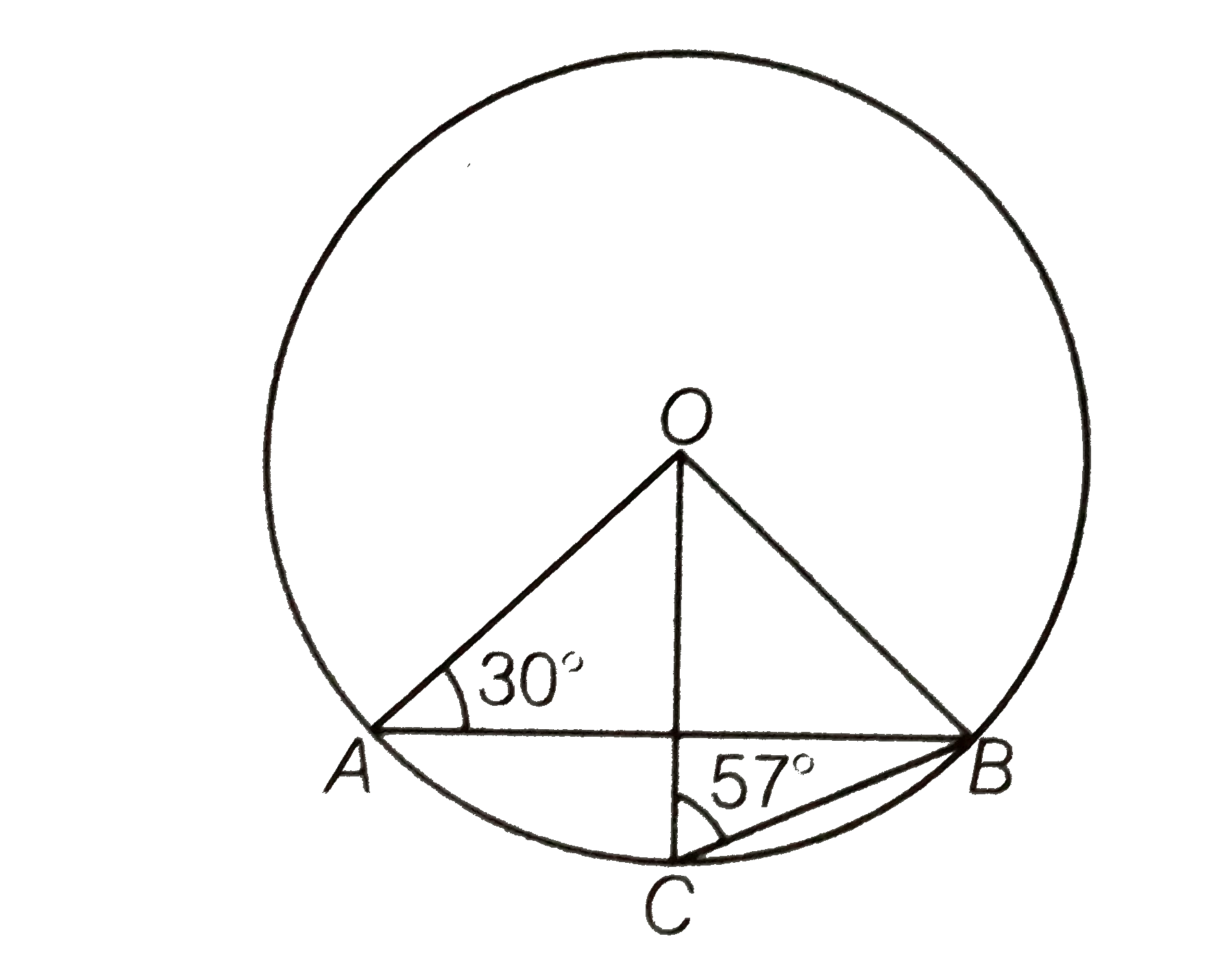
In figure, ∠OAB=30∘and∠OCB=57∘. Find ∠BOC
Video Solution
Text Solution
Given,∠OAB=30∘and∠OCB=57∘
In ΔAOB,AO=OB [both are the radius of a circle]
⇒∠OBA=∠BAO=30∘
[angles opposite to equal sides are equal]
InΔAOB,
⇒∠AOB+∠OBA+∠BAO=180∘ [by angle sum property of a triangle]
∴∠AOB+30∘+30∘=180∘
∴∠AOB=180∘−2(30∘)
=180∘−60∘=120∘ ...(i)
Now, in ΔOCB,
OC=OB [both are the radius of a circle]
⇒∠OBC=∠OCB=57∘
[angle opposite to equal sides are equal]
In ΔOCB,
∠COB+∠OCB+∠CBO=180∘ [by angle sum property of triangle]
∴∠COB=180∘−(∠OCB+∠OBC)
=180∘−(57∘+57∘)
=180∘−114∘=66∘ ...(ii)
Form Eq. (i), ∠AOB=120∘
⇒∠AOC+∠COB=120∘
⇒∠AOC+66∘=120∘ [from Eq. (ii)]
∴∠AOC=120∘−66∘=54∘
|
Topper's Solved these Questions
- CIRCLESBOOK - NCERT EXEMPLARCHAPTER - CIRCLESEXERCISE - Exercise 10.4
2 Videos
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLARCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Areas Of Parallelograms And Triangles
34 Videos
- CONSTRUCTIONSBOOK - NCERT EXEMPLARCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions
5 Videos
Similar Questions
Knowledge Check
In the following figure ∠B=70∘ and ∠C=30∘.BOandCO are the angle bisectors of ∠ABCand∠ACB. Find the value of ∠BOC:
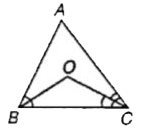 A30∘B40∘C120∘D130∘
A30∘B40∘C120∘D130∘
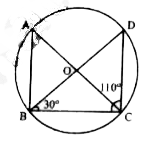
In this figure ∠DBC=30∘and∠BCD=110∘. Find ∠BAC
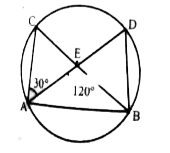
View SolutionIn the figure, ∠CAE=30∘and∠AEB=120∘. Find ∠ADB
View SolutionIn the given figure, ∠OAB=110∘ and ∠BCD=130∘ then ∠ABC is equal to
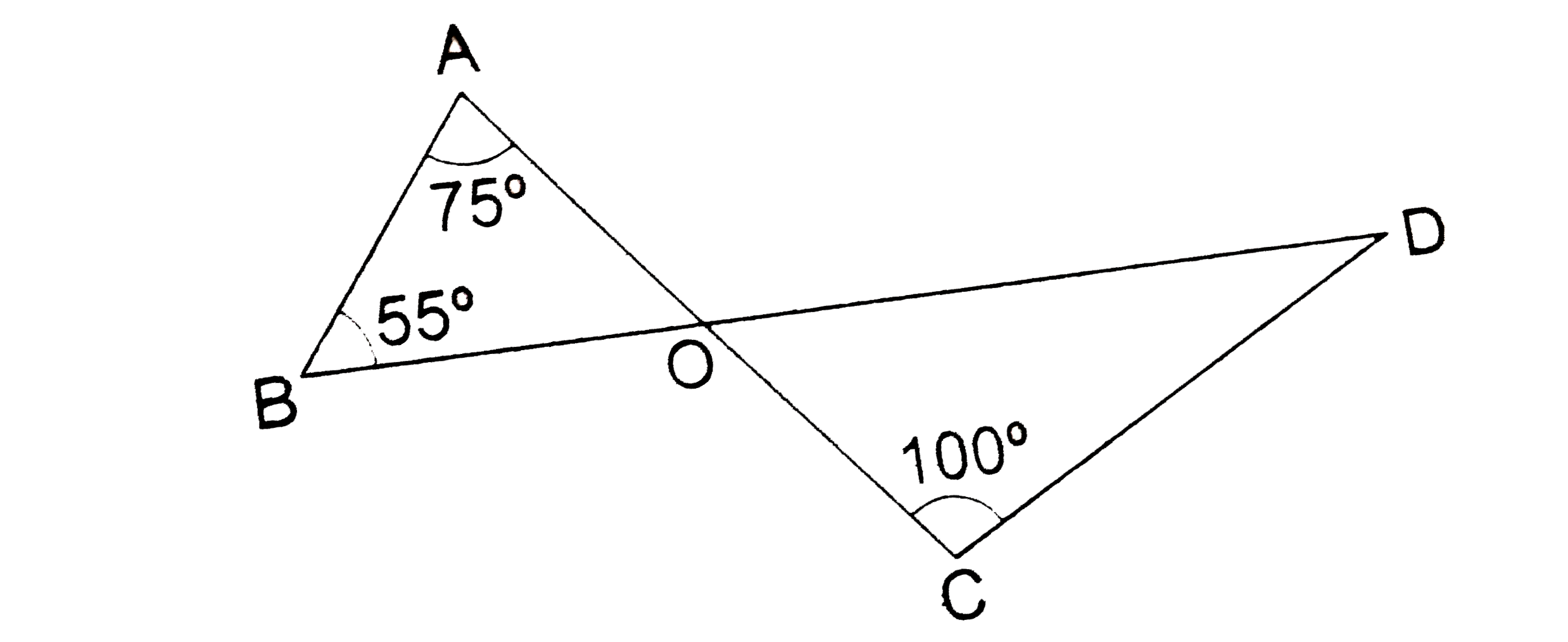
View SolutionIn the given figure, ∠OAB=75∘,∠OBA=55∘ and∠OCD=100∘. Then, ∠ODC=?
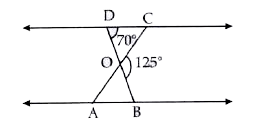
View SolutionIn the figure below ΔODC~ΔOBA,∠BOC=125∘ and ∠CDO=70∘ . Find ∠DOC,∠DCO and ∠OAB.
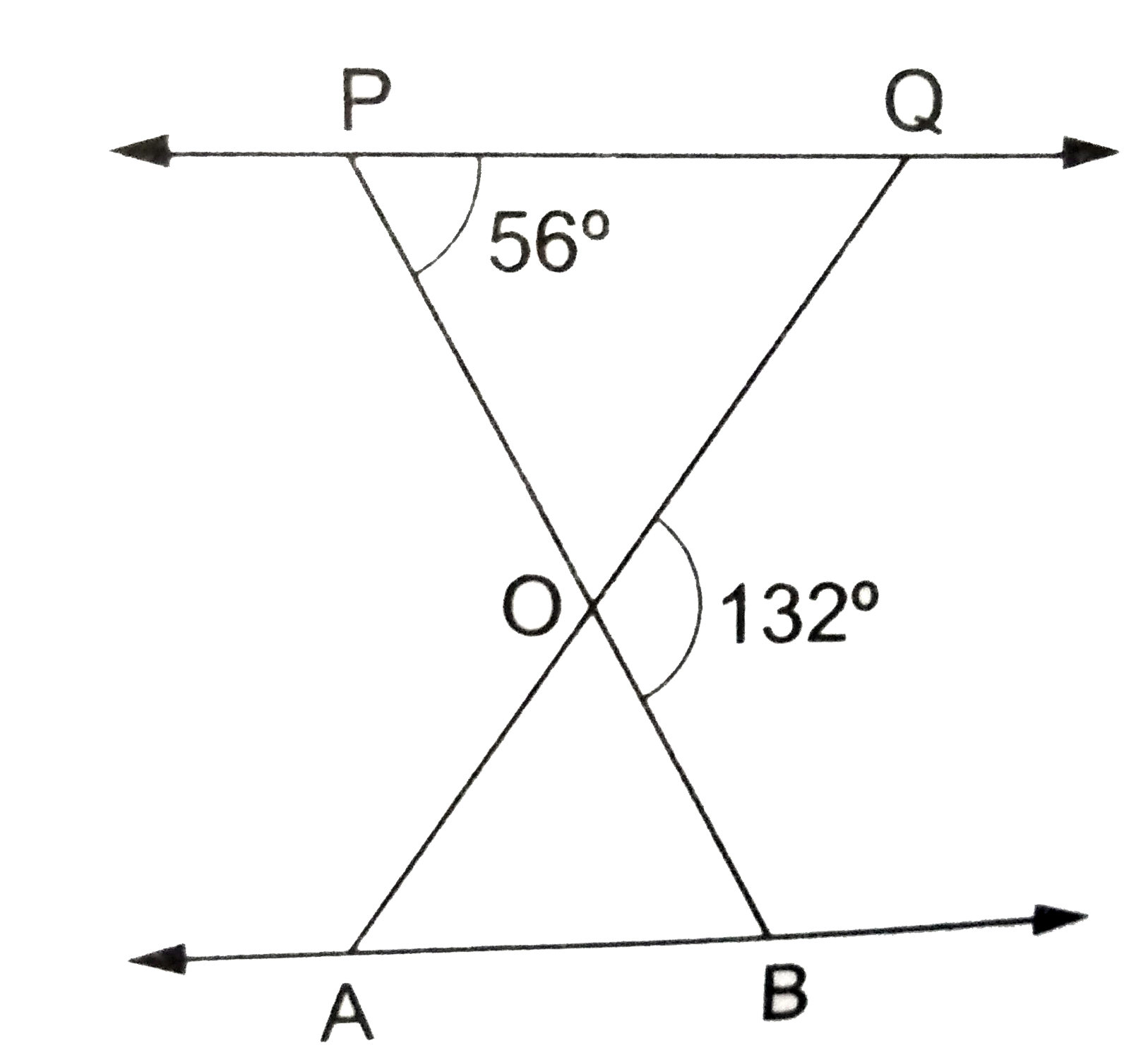
View SolutionIn the given figure, ΔOQP~ΔOAB,∠OPQ=56∘and∠BOQ=132∘. Find ∠OAB.
View SolutionIn the given figure, AOB is a straight line. If ∠AOC=(3x+10)∘ and ∠BOC=(4x−26)∘, then ∠BOC= ?

View Solution