Question

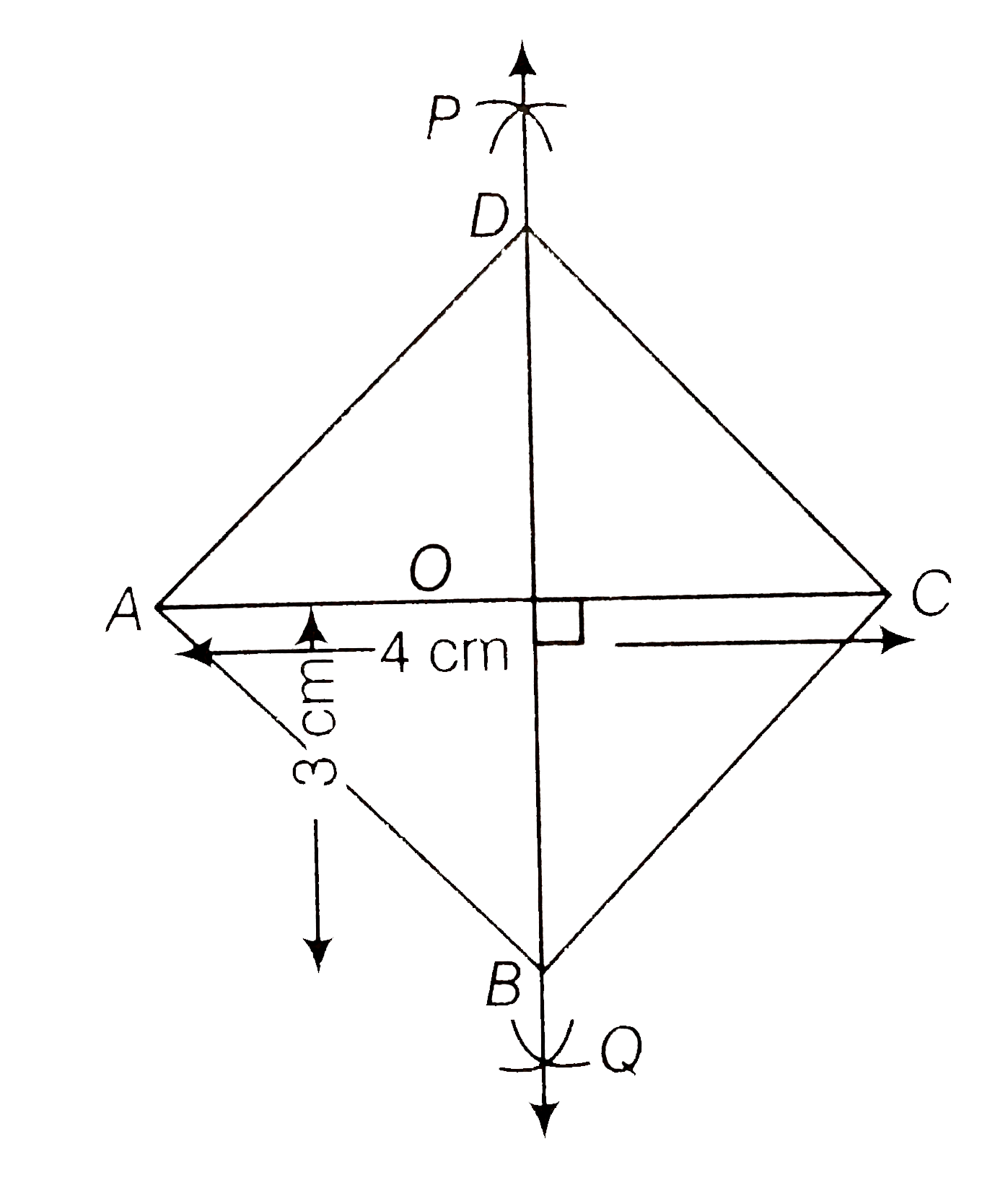
A rhombus whose diagonals are $4cm$ and $6cm$ in lengths.

Explanation

We know that , all sides of a rhombus are equal and the diagonals of a rhombus are equal and the diagonals of a rhombus are perpendicular bisectors of one another. So, to construct a rhombus whose diagonals are `4cm` and `6cm` use the following stegs.
(i) Draw the diagonal say `AC = 4cm`
(ii) Taking `A` and `C` as centres and radius more than `(1)/(2)AC` draw arcs on both sides of the line segment AC to intersect each other.
(iii) Cut both arcs intersect each other.
(iv) Let PQ intersect AC at the point O. Thus , PQ is perpendicular bisector of AC.
(v) Cut off `3cm` lengths from `OP` and OQ, then we get points B and D.
(vi) Now , join `AB, BC, CD`, and `DA`.
Thus, `ABCD` is the required rhombus.
Justification
Since, D and B lie on perpendicular bisector of AC.
DA = DC and BA = BC ....(i)
[since, every point on perpendicular of line segment is equidistant from end points of line segment]
Now, `angleDOC = 90^(@)`
Also, OD = OB = 3cm
Thus , AC is perpendicular bisector or BD.
CD = CB ....(ii)
From Eqs. (i) and (ii), AB = BC = CD = DA
Hence , ABCD is a rhombus.