The area of an isosceles triangle having base $2 c m$ and the length of one of the equal sides $4 c m$ , is

A

$\sqrt{15} c m^{2}$

B

$\sqrt{\frac{15}{2}} c m^{2}$

C

$2 \sqrt{15} c m^{2}$

D

$4 \sqrt{15} c m^{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

(a) Let $B A C$ be an isosceles triangle in which $A B = A C = 4 c m$ and $B C = 2 c m .$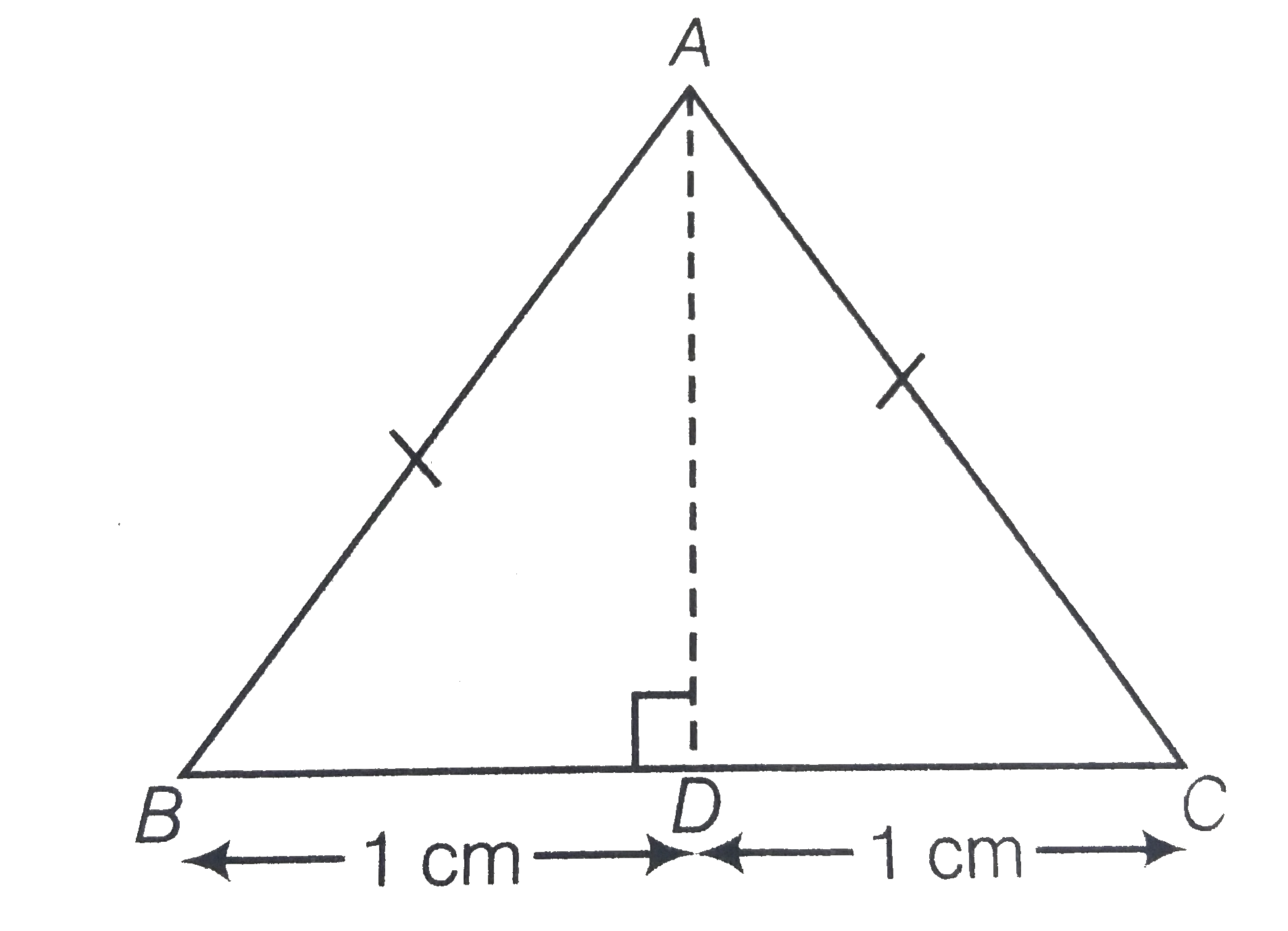
In right angied $△ A D B$ ,
$A B^{2} = A D^{2} + B D^{2}$
$\Rightarrow {(4)}^{2} = A D^{2} + 1$
$\Rightarrow A D^{2} = 16 - 1$
$\Rightarrow A D^{2} = 15$
$∴ A D = \sqrt{15} c m$
$[taking positive square root because length is always positive]$
$∴ Area of △ A B C = \frac{1}{2} \times B C \times A D [∵ area of triangle = \frac{1}{2} (base \times height)]$
$= \frac{1}{2} \times 2 \times \sqrt{15} = \sqrt{15} c m^{2}$ Alternate Method
We know that,
$Area of an isosceles triangle = \frac{a}{4} \sqrt{4 b^{2} - a^{2}}$
where, b is the length of equal sides and a sides and a is the length of the base.
Here, the length of side be b=4 cm and a=2 cm
$∴ Area of an isosceles triangle = \frac{2 \sqrt{4 {(4)}^{2} - 4}}{4} = \frac{\sqrt{64 - 4}}{2}$
$= \frac{\sqrt{60}}{2} = \frac{2 \sqrt{15}}{2} = \sqrt{15} c m^{2}$

|

Updated on:21/07/2023

Class 9 MATHS HERONS FORMULA

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The area of an isosceles triangle having base $2 c m$ and the length of one of the equal sides $4 c m$ , is
A $\sqrt{15} c m^{2}$
B $\sqrt{\frac{15}{2}} c m^{2}$
C $2 \sqrt{15} c m^{2}$
D $4 \sqrt{15} c m^{2}$
Question 2 - Select One
The internal base of an isosceles triangle can be whose area is $60 c m^{2}$ and the length of one of the equal sides is 13 cm :
A20 cm
B10 cm
C16 cm
Ddata insufficient .
Question 3 - Select One
The internal base of an isosceles triangle can be whose area is $60 c m^{2}$ and the length of one of the equal sides is 13 cm :
A20 m
B10 cm
C16 cm
Ddata insufficient

NCERT EXEMPLAR-HERON'S FORMULA-Herons Formula

Home
Ask Doubt
Profile