A cavity of radius b is made in a disc of mass M, radius R, as ahown in fig. Find the new COM-
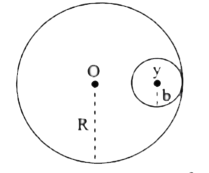
−b2R+b
−b2R−b
−R2R+b
−R3R+b
The correct Answer is:A
xCM=M(0)−Mb2R2(R−b)M−Mb2R2
=−b2R+b
Topper's Solved these Questions
Similar Questions
A spherical cavity of radius R2 is made in a sphere of radius R and mass M. The centre of the cavity is at a distance R2 from the centre of the sphere. The intensity of gravitational field at the centre of cavity is GMnR2. Find n.
View SolutionA circular disc of mass M1 and radius R, initially moving, With a constant angular speed ω is gently placed coaxially on a stationary circular disc of mass M2 and radius R, as shown in Fig. There is a frictional force between the two discs.
If disc M2 is placed on a smooth surface, then 'determine' the final angular speed of each disc.
b. Determine the work done by friction.
c. Determine the frictional loss in kinetic energy. i.e. △K/Ki
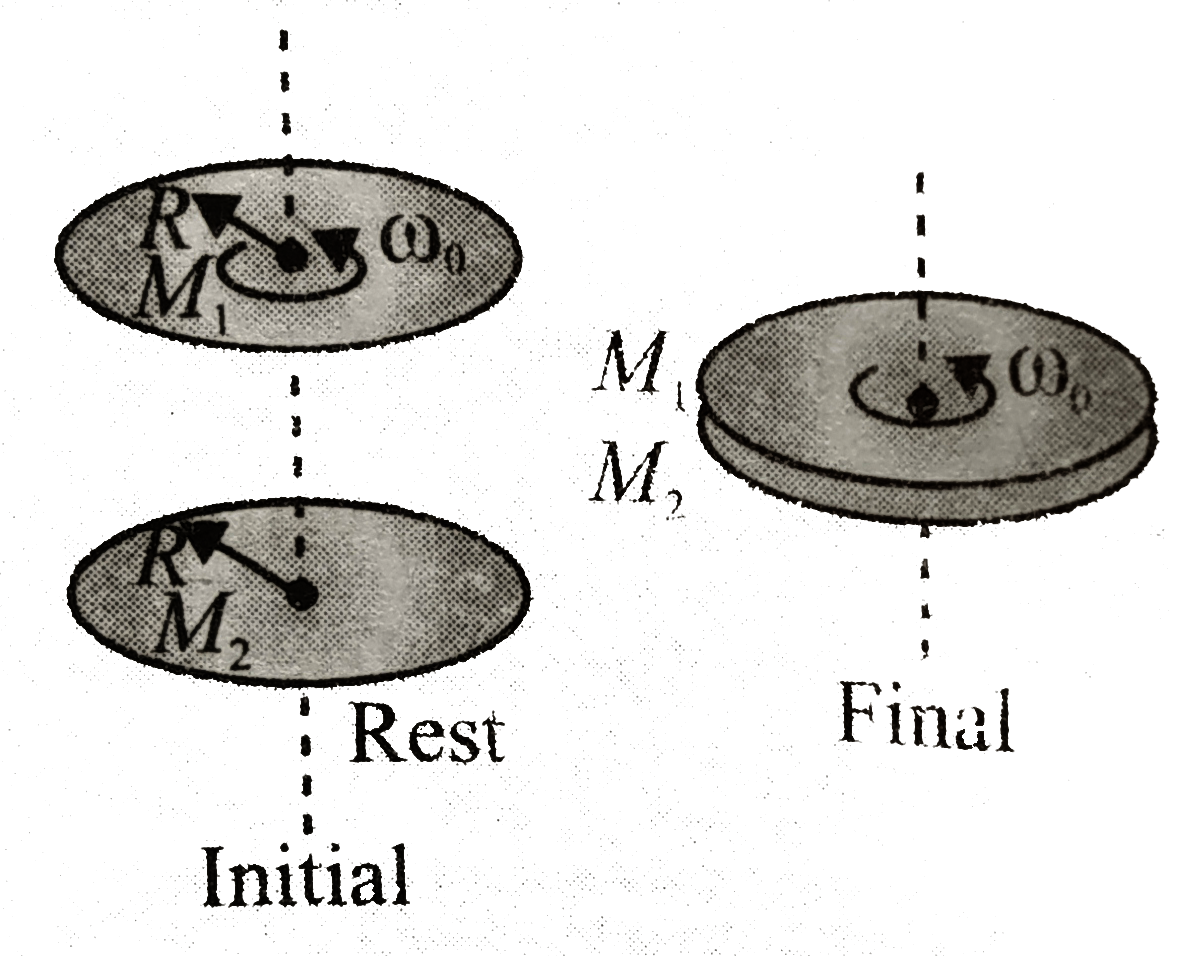
View Solution
Knowledge Check
A cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of a mass 'm' at a distance R/2 from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here g=GM/R2, where M is the mass of the solid sphere]
Amg2B3mg8Cmg16Dnone of theseA small hole is made in a disc of mass M and radius R at a distance R/4 from centre. The disc is supported on a horizontal peg through this hole. The moment of inertia of the disc about horizontal peg is
AMR29B516MR2C916MR2D54MR2A disc of radius r is removed from the centre of a disc of mass M and radius R. The M.I. About the axis through the centre and normal to the plane will be:
AM(R2−r2)/2BM(R2+r2)/2CM(R4−r4)/2R2DM(R2)/2
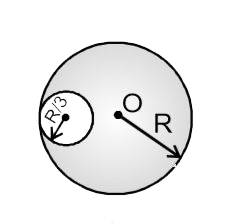
A thin disc of mass 9M and radius R is given.Now a disc of radius (R/3) is cut as shown in figure.The new position of C .m from orgin will be :-
View SolutionA uniform disc of radius R has a round disc of radius R/3 cut as shown in Fig. The mass of the remaining (shaded) portion of the disc equals M. Find the moment of inertia of such a disc relative to the axis passing through geometrical centre of original disc and perpendicular to the plane of the disc.
View SolutionA circular metallic disc of radius R has a small circular cavity of radius r as shown in figure. On heating the system :

View SolutionA spherical cavity of radius r is made in a conducting sphere of radius 2 r.A charge q is kept at the centre of cavity as shown in the figure.Find the magnitude of the total electric field at (4r 0) .
View SolutionA circular metallic disc of radius R has a small circular cavity of radius r as shown in figure. On heating the system

View Solution
