Figure shows a coil of single turn wound on a sphere of radius R and mass m. The plane of the coil is parallel to the plane and lies in the equatorial plane of the sphere. What is the value of B if the sphere is in equilibrium when current in the coil is I?
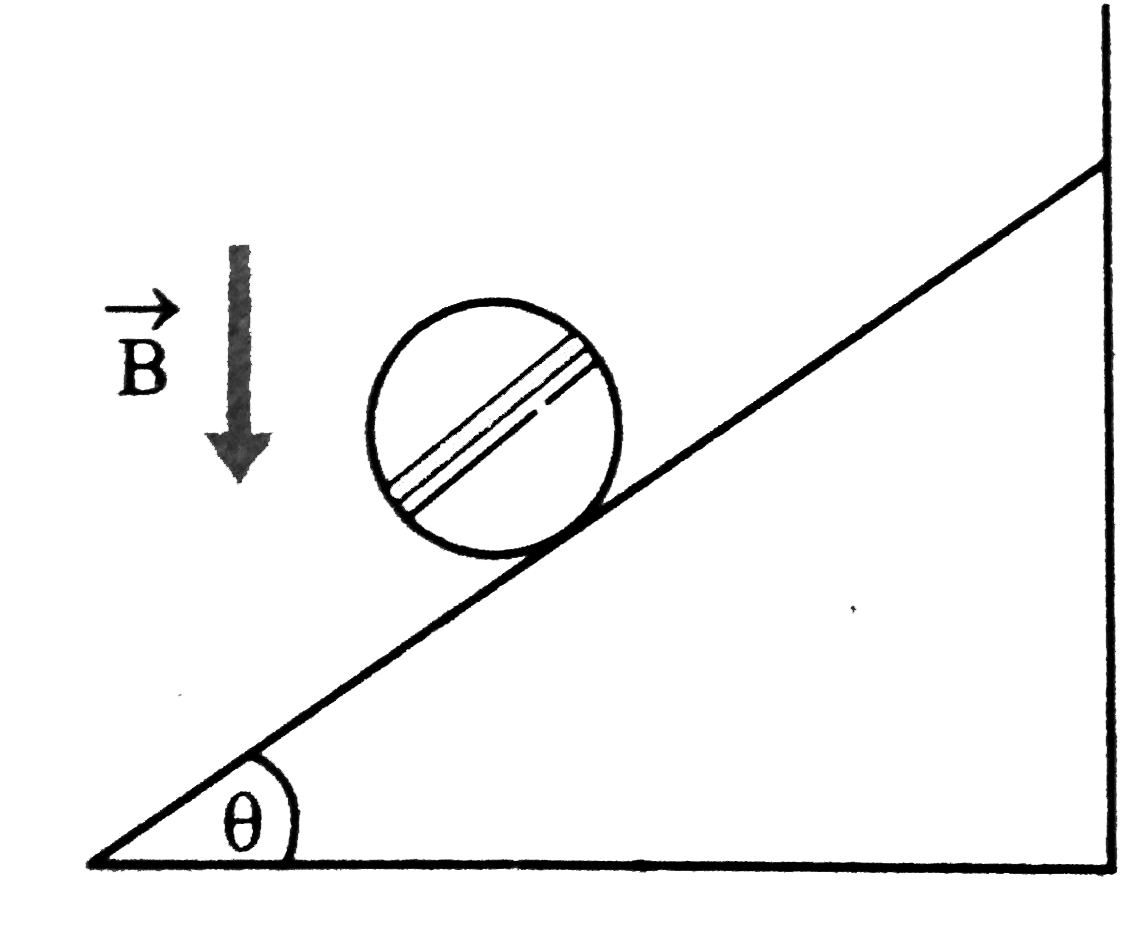
mgcosθπiR
mgπiR
mgtanθπiR
mgsinθπiR
The correct Answer is:B
Step by step video, text & image solution for Figure shows a coil of single turn wound on a sphere of radius R and mass m. The plane of the coil is parallel to the plane and lies in the equatorial plane of the sphere. What is the value of B if the sphere is in equilibrium when current in the coil is I? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - MAGNETISM EXERCISE - EXERCISE-2 (Level-I)40videos
MAGNETISM
- BOOK - MOTIONCHAPTER - MAGNETISM EXERCISE - EXERCISE-2 (Level-II)15videos
MAGNETISM
- BOOK - MOTIONCHAPTER - MAGNETISM EXERCISE - EXERCISE-4 (LEVEL-II)40videos
MAGNETISM
- BOOK - MOTIONCHAPTER - LOGIC GATESEXERCISE - EXERCISE - 210videos
LOGIC GATES
- BOOK - MOTIONCHAPTER - MAGNETISM -1EXERCISE - Exercise - 3 SECTION -A56videos
MAGNETISM -1
Similar Questions
If a sphere of radius 10 cm is intersected by a plane at a distance 8 cm from its centre, what is the radius of the curve of intersection of the plane and the sphere?
View SolutionA thin wire is wound very tightly in one layer on the surface of a sphere of paramagnetic material (μr≈1). The planes of all the turns can be assumed to be perpendicular to the same diameter of the sphere. The turns over the entire surface of the sphere. The radius of the sphere is R, the total number of turns is N, and the current in the winding is I. Find the magnetic induction at the centre of the sphere. (Given μ0NI=20R)
View Solution
Knowledge Check
- Question 1 - Select One
In Fig. a coil of single turn is wound on a sphere of radius r and mass m. The plane of the coil is parallel to the inclined plane and lies in the equatorial plane of the sphere. If the sphere is in rotational equilibrium, the value of B is [Current in the coil is i]
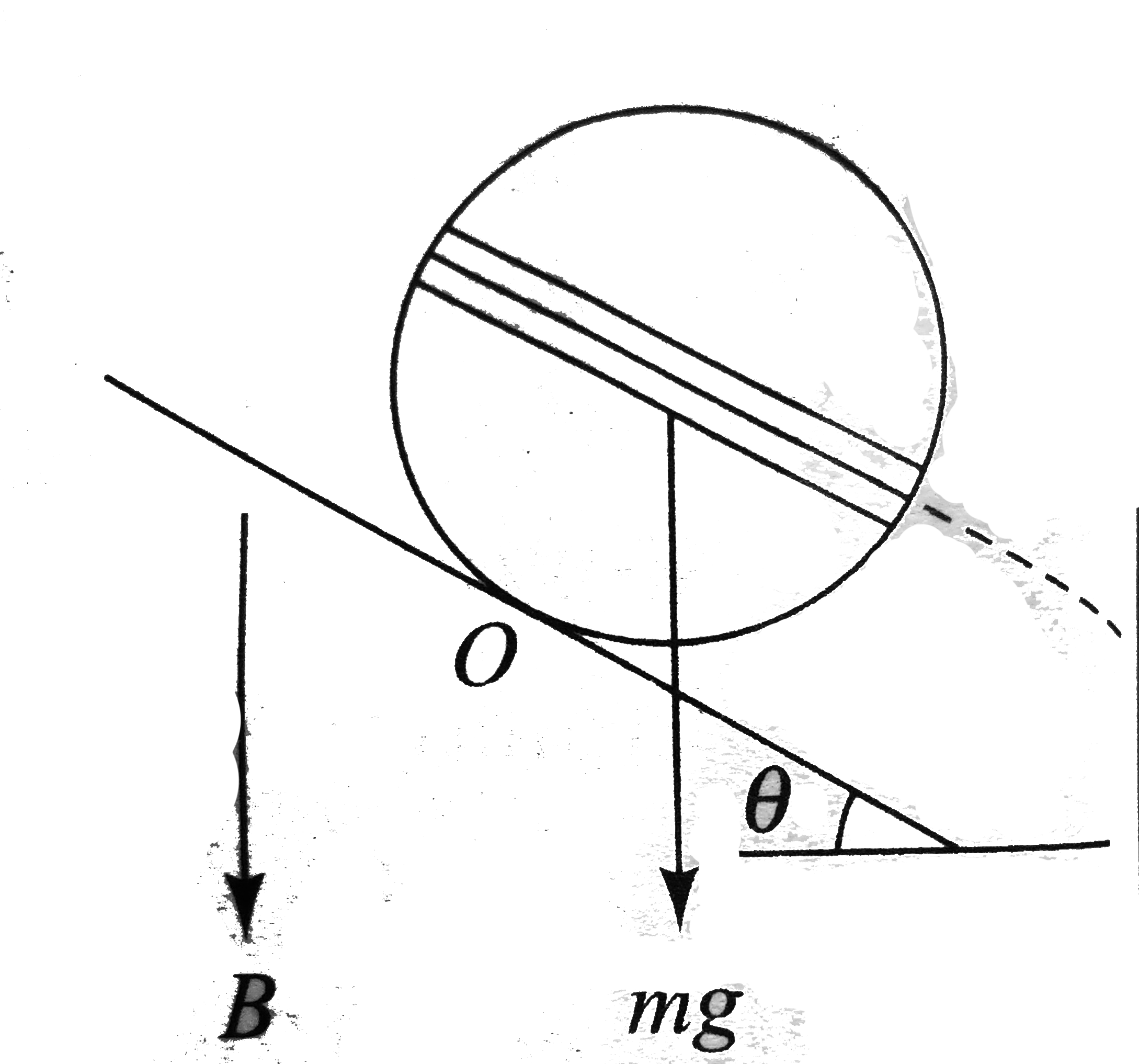 AmgπirBmgsinθπiCmgsinθπiDNone of these
AmgπirBmgsinθπiCmgsinθπiDNone of these - Question 2 - Select One
Current I is flowing through a circular coil of radius r. It is placed in a magnetic field B0 in such a way that the plane of the circular coil is perpendicular to B0. The force acting in it will be -
AParallel to BBIs perpendicular to BCAt45∘ with BDAt 60∘ with B - Question 3 - Select One
Three mutually, tangent spheres of radius 1 rest on a horizontal plane. A sphere of radius 2 rests on them. What is the distance from the plane to the top of the larger sphere?
A3+√302B3+√693C3+√1234D529
A coil is placed in a constant magnetic field. The magnetic field is parallel to the plane of the coil as shown in Fig. 3.28. Find the emf induced in the coil if B increasing.
 View Solution
View SolutionA solid sphere of mass m rolls without slipping on an inclined plane of inclination θ. The linear acceleration of the sphere is
View SolutionA current i flows in a circular coil of radius r. If the coil is placed in a uniform magnetic field B with its plane parallel to the field, magnitude of the torque that acts on the coil is
View SolutionA current i flows in a circular coil of radius r. If the coil is placed in a uniform magnetic field B with its plane parallel to the field, magnitude of the torque that acts on the coil is
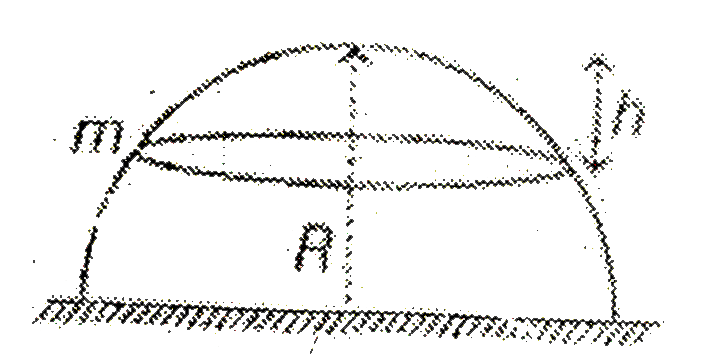
View SolutionA unofrom rope of mass m is placeced on a smooth fixed sphere of radius R as shown in the figure .Find the tension T in the rope when it is in a horizontal plane at a vertical distance h=R/2 below the top of the sphere .
 View Solution
View Solution

