In the diagram shown, a wire carries current I. What is the value of the ∮→B.d→l (as in Ampere's law) on the helical loop shown in the figure. The integration is done in the sense shown. The loop has N turns and part of helical loop on which arrows are drawn outside the plane of paper.
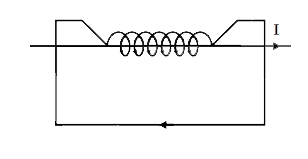
−μ0(NI)
μ0(I)
μ0(NI)
zero
The correct Answer is:B
Topper's Solved these Questions
- MAGNETISM BOOK - MOTIONCHAPTER - MAGNETISM EXERCISE - EXERCISE-2 (Level-II)
15 Videos
- MAGNETISM BOOK - MOTIONCHAPTER - MAGNETISM EXERCISE - EXERCISE-3 (Level-I)
46 Videos
- MAGNETISM BOOK - MOTIONCHAPTER - MAGNETISM EXERCISE - EXERCISE-1
50 Videos
- LOGIC GATESBOOK - MOTIONCHAPTER - LOGIC GATESEXERCISE - EXERCISE - 2
10 Videos
- MAGNETISM -1BOOK - MOTIONCHAPTER - MAGNETISM -1EXERCISE - Exercise - 3 SECTION -A
56 Videos
Similar Questions
Knowledge Check
In the diagram shown, a wire carriers current I. The loop has N turns and part of helical loop on which arrows are drawn is outside the plane of paper. What is the value of the ∮→B.→dl (as in Ampere's law) on the helical loop shown in the figure?
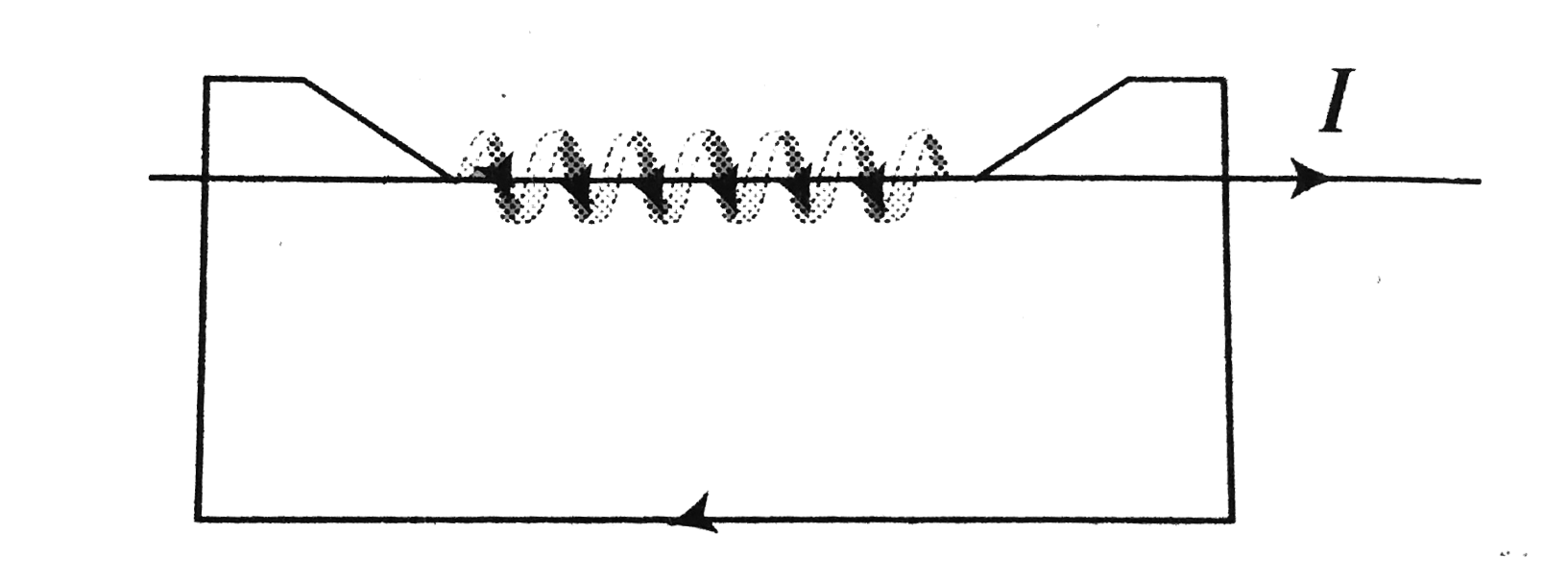 A−μ0(NI)Bμ0(I)Cμ0(NI)DZero
A−μ0(NI)Bμ0(I)Cμ0(NI)DZeroThe wire loop shown in figure carries a current as shown. The magnetic field at the centre O is ,
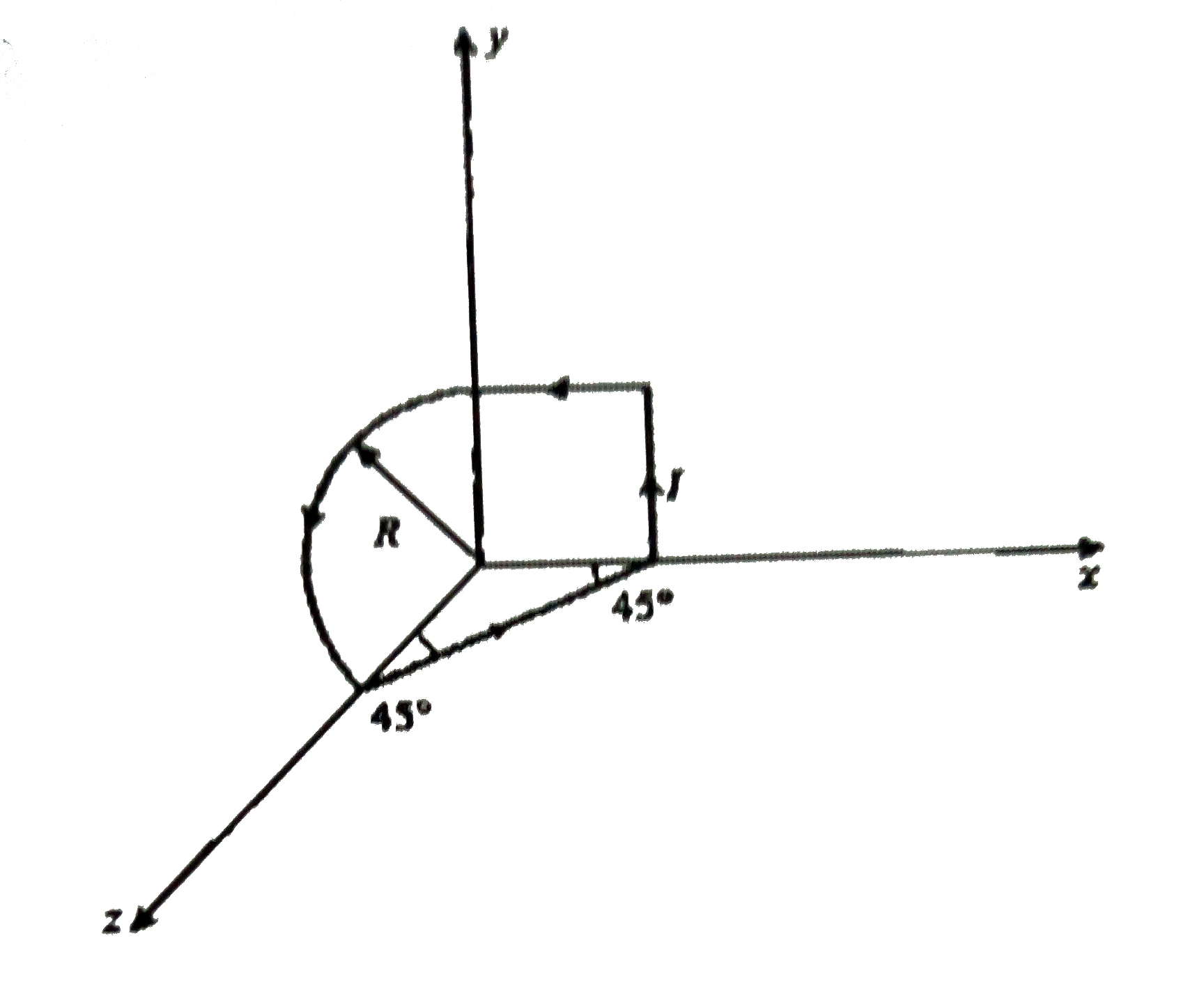
 AzeroBμ0I4(1R1−1R2)Cμ0I4(1R2+1R1)Dμ0I2(1R1−1R2)
AzeroBμ0I4(1R1−1R2)Cμ0I4(1R2+1R1)Dμ0I2(1R1−1R2)The magnetic moment of the current carrying loop shown in the figure is equal to
 Al(b2+2ab)θ2BlabθCl(a2+ba)θ2DNone of the above
Al(b2+2ab)θ2BlabθCl(a2+ba)θ2DNone of the above
Write equation for Ampere's circuital law for the Amperian loop shown (traversed in the direction shown by arrow marks put on it)
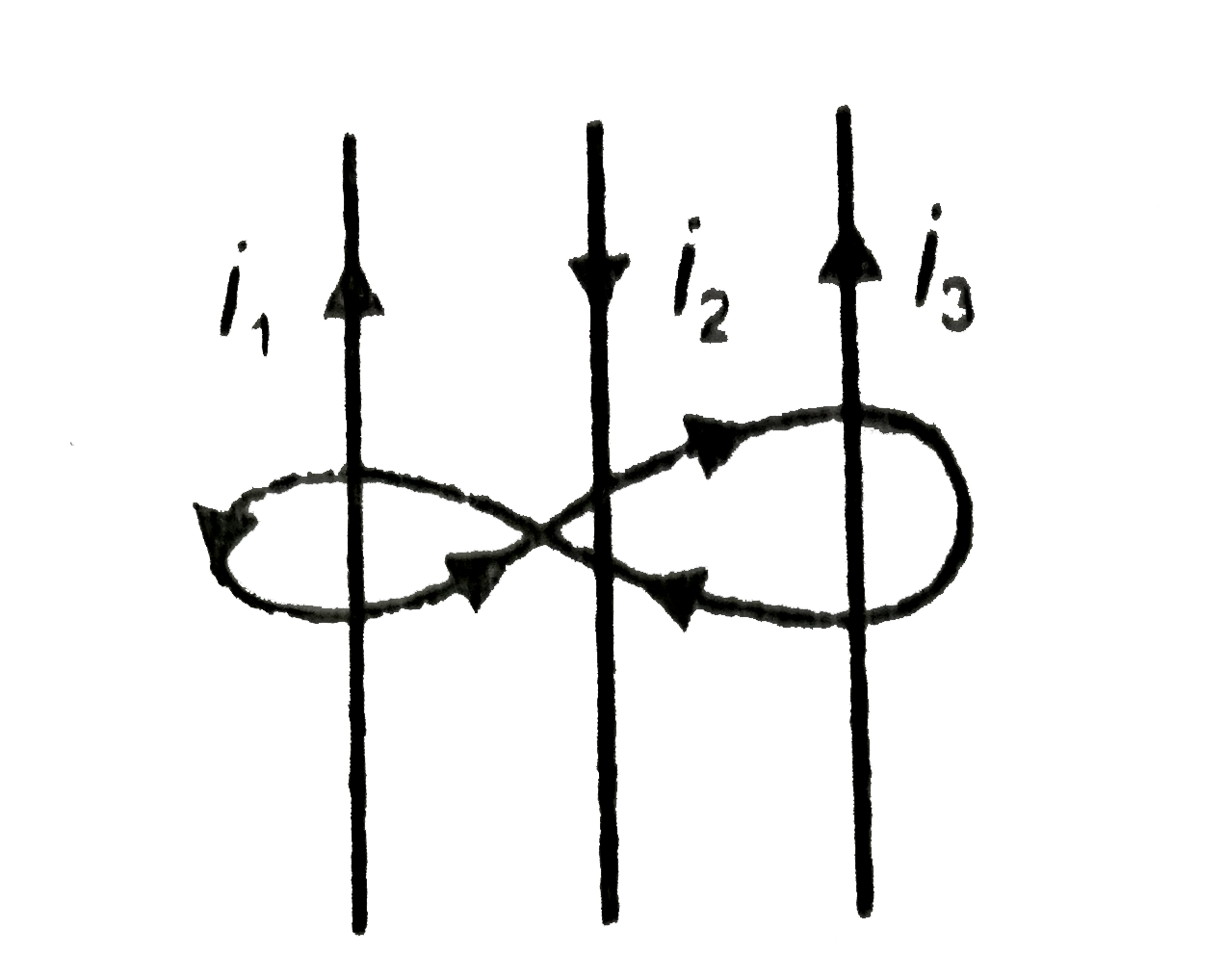
View SolutionWrite equation for Ampere's circuital law for the Amperian loop shown (traversed in the direction shown by arrow marks put on it)

View SolutionWrite equation for Ampere's circuital law for the Amperial loop as shown below
(Traverse in the direction shown by arrow mark buton it )
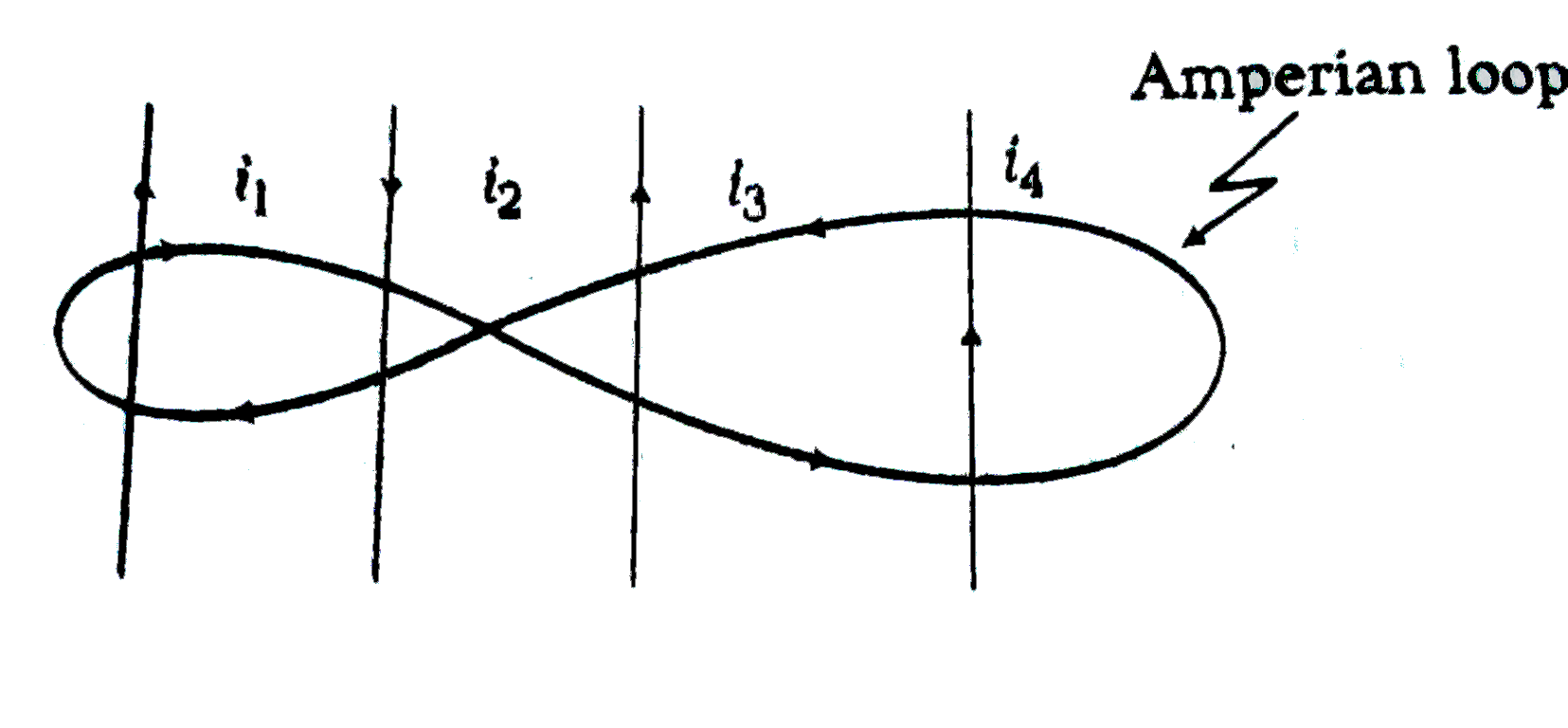
View SolutionA square loop of wire carrying current I is lying in the plane of paper as shown in Fig. 1.141. The magnetic field is present in the region as shown. The loop will tend to rotate
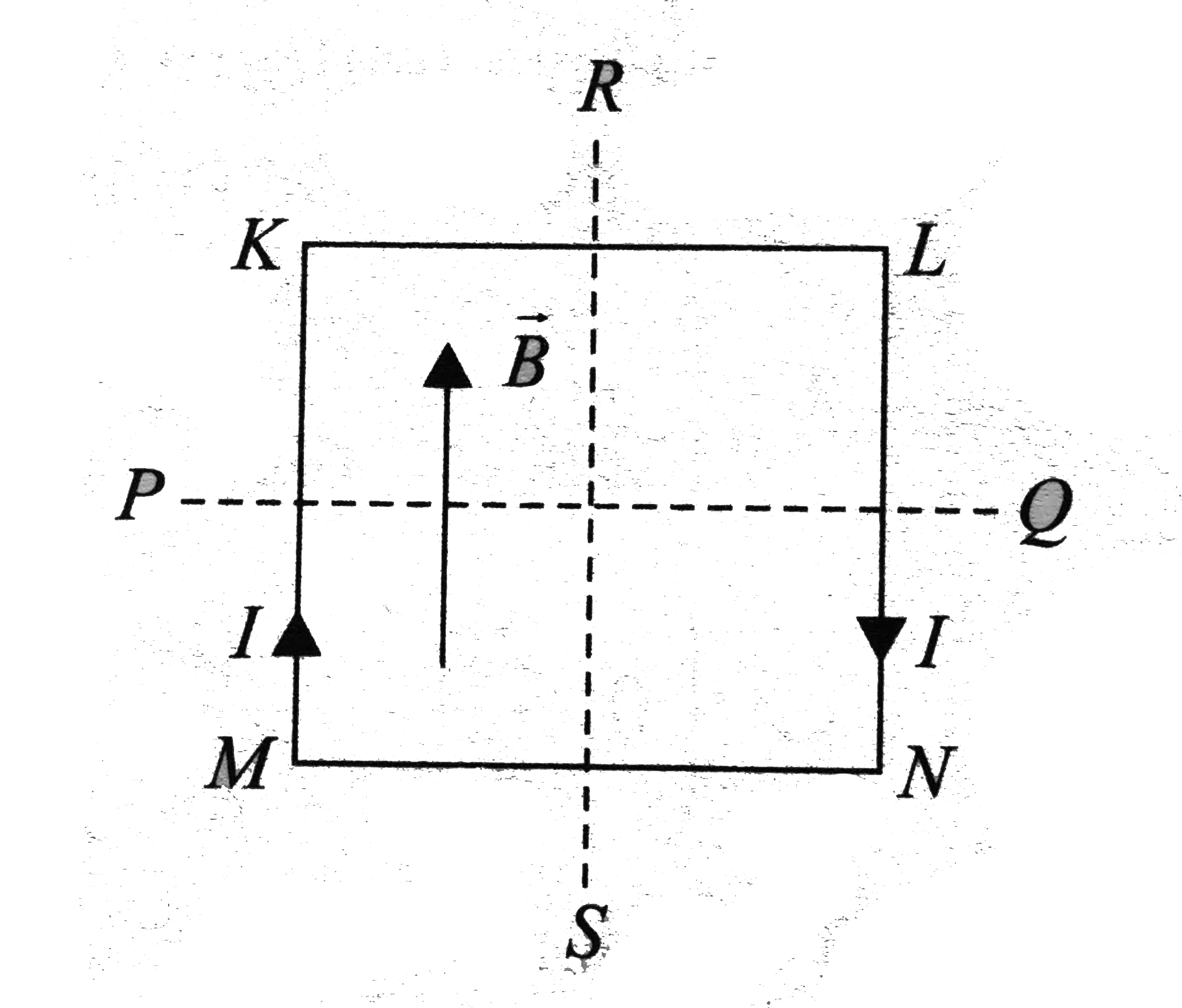
View SolutionA square loop of wire carrying current I is lying in the plane of paper as shown in Fig. 1.141. The magnetic field is present in the region as shown. The loop will tend to rotate

View Solution