A current I, indicated by the crosses in fig. is established in a strip of copper of height h and width w. A uniform field of magnetic induction B is applied at right angles to the strip.
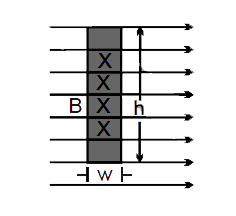
What is the voltage V necessary between two sides of the conductor in order to create this field E?
5.7×10−6V (top+, bottom-)
Topper's Solved these Questions
- MAGNETISM BOOK - MOTIONCHAPTER - MAGNETISM EXERCISE - EXERCISE-3 (Level-II)
23 Videos
- MAGNETISM BOOK - MOTIONCHAPTER - MAGNETISM EXERCISE - EXERCISE-4 (LEVEL-I)
33 Videos
- MAGNETISM BOOK - MOTIONCHAPTER - MAGNETISM EXERCISE - EXERCISE-2 (Level-II)
15 Videos
- LOGIC GATESBOOK - MOTIONCHAPTER - LOGIC GATESEXERCISE - EXERCISE - 2
10 Videos
- MAGNETISM -1BOOK - MOTIONCHAPTER - MAGNETISM -1EXERCISE - Exercise - 3 SECTION -A
56 Videos
Similar Questions
A current I, indicated by the crosses in fig. is established in a strip of copper of height h and width w. A uniform field of magnetic induction B is applied at right angles to the strip.
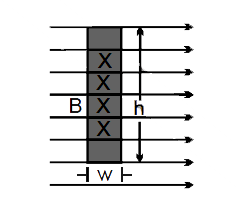
Calculate the drift speed vd for the electrons.
View SolutionA current I, indicated by the crosses in fig. is established in a strip of copper of height h and width w. A uniform field of magnetic induction B is applied at right angles to the strip.
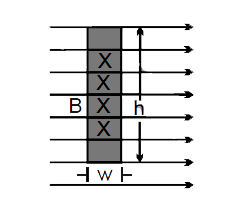
What are the magnitude and direction of the magnetic force F acting on the electrons?
View Solution
Knowledge Check
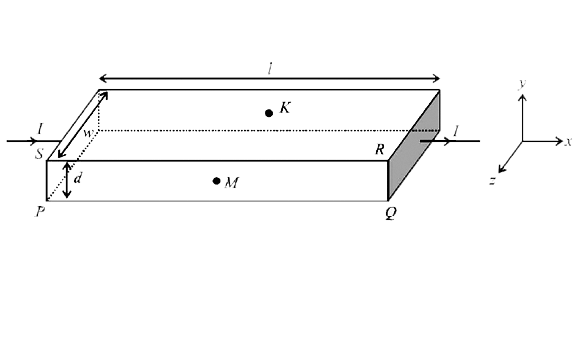
In a thin rectangular metallic strip a constant current I flows along the positive x−direction,asshown∈thefigure.The≤n>h,whandthick≠ssofthestriparel, w and d,respectively.<br>Auniformmag≠ticfieldvec(B)isappliedonthestripalongthepositivey- direction.Due→this,thechar≥carriersexperiencea≠tdef≤ctionalongthez- direction.Thisrest–s∈auμlationofchar≥carriersonthesurfacePQRSansdapperanceofequalandoppositechar≥sonthefaceopposite→PQRS.Apotentiald⇔erencealongthez-directionisthusdeveloped.Char≥auμlationcontiuesuntillthemag≠ticforceisbalancedbythee≤ctricforce.Thecurrentisas∑ed→beuniformlydistributedonthecross−sectionofthestripandcarriedbye≤ctrons.<br>Consrtwod⇔erentmηllicstrips(1 and 2)ofsamedimensionsn_(1) and n_(2),repectrively.Strip1isplaced∈mag≠ticfieldB_(1)andstrip2isplaced∈mag≠ticfieldB_(2),⊥halongpositive y- directions.Then V_(1) and V_(2)arethepotentiald⇔erencesdevelopedbetweenK and M∈strips1and2,respectively.As∑∈gtˆthecurrentI is the same for both the strips, the correct option(s) is (are)
 AIf B1=B2andn1=2n2,thenV2=2V1BIf B1=B2andn1=2n2,thenV2=V1CIf B1=2B2andn1=2n2,thenV2=0.5V1DIf B1=2B2andn1=2n2,thenV2=V1
AIf B1=B2andn1=2n2,thenV2=2V1BIf B1=B2andn1=2n2,thenV2=V1CIf B1=2B2andn1=2n2,thenV2=0.5V1DIf B1=2B2andn1=2n2,thenV2=V1In a thin rectangular metallic strip a constant current I flows along the positive x−direction,asshown∈thefigure.The≤n>h,whandthick≠ssofthestriparel, w and d,respectively.<br>Auniformmag≠ticfieldvec(B)isappliedonthestripalongthepositivey- direction.Due→this,thechar≥carriersexperiencea≠tdef≤ctionalongthez- direction.Thisrest–s∈auμlationofchar≥carriersonthesurfacePQRSansdapperanceofequalandoppositechar≥sonthefaceopposite→PQRS.Apotentiald⇔erencealongthez-directionisthusdeveloped.Char≥auμlationcontiuesuntillthemag≠ticforceisbalancedbythee≤ctricforce.Thecurrentisas∑ed→beuniformlydistributedonthecross−sectionofthestripandcarriedbye≤ctrons.<br>Consrtwod⇔erentmηllicstrips(1 and 2)ofthesamematerial.Their≤n>hsarethesame,whsarew_(1) and w_(2)andthick≠ssared_(1) and d_(2)respectively.Twop∮sK and Maresymmetricallylocatedontheoppositefacesparal≤l→the x-ypla≠(seefigure).V_(1) and V_(2)arethepotentiald⇔erencesbetweenK and M∈strips 1 and 2,respectively.Then,foragivencurrentIflow∈gthroughthem∈agivenmag≠ticfieldstren>hB, the correct statement(s) is (are)
 AIf w1=w2andd1=2d2,thenV2=2V1BIf w1=w2andd1=2d2,thenV2=V1CIf w1=2w2andd1=d2,thenV2=2V1DIf w1=2w2andd1=2d2,thenV2=V1
AIf w1=w2andd1=2d2,thenV2=2V1BIf w1=w2andd1=2d2,thenV2=V1CIf w1=2w2andd1=d2,thenV2=2V1DIf w1=2w2andd1=2d2,thenV2=V1
A current I, indicated by the crosses in fig. is established in a strip of copper of height h and width w. A uniform field of magnetic induction B is applied at right angles to the strip.
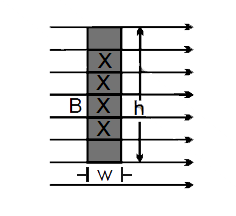
What would the magnitude & direction of homogeneous electric field E have to be in order to counter balance the effect of the magnetic field?
View SolutionA current I, indicated by the crosses in fig. is established in a strip of copper of height h and width w. A uniform field of magnetic induction B is applied at right angles to the strip.
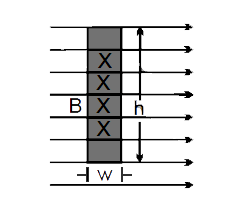
If no electric field is applied form the outside the electrons will be pushed somewhat to one side & thereforce will give rise to a uniform electric field EH across the conductor untill the force of this electrostatic field EH balance the magnetic forces encountered in part (b). What will be magnitude and direction of the field EH? Assume that n, the number of conduction electrons per unit volume, is 1.1×1029/m3 & that h=0.02 meter, w=0.1cm, i=50 amp, & B=2webers/meter2.
View SolutionA current i, indicated by the crosses in figure, is established in a strip of copper of height h and width w. A uniform field of magnetic induction B is applied at right angle to the strip.
(a) Calculate the drift velocity vd of the electrons.
(b) What are the magnitude and direction of the magnetic force F acting on the electrons?
(c) What should the magnitude and direction of a homogeneous electric field E be in order to counterbalance the effect of mangetic field?
(d) Calculate voltage V necessary between two sides of the conductor in order to creat this field E Between which sides of the conductor would this voltage have to be applied?
(e) If no electric field is applied from the outside, the electrons will be pushed somewhat to one side and therefore will give rise to a uniform electric field EH across the conductor until the forces of this electrostatic field EH balance the magnetic forces encountered in part (b). What will be the magnitude and direction of field EH?
Assume that n, the number of conductor electrons per unit volume is 1.1×1029m−3,h=0.02m,w=0.1cm,i=50A,andB=2T.

View SolutionA current i, indicated by the crosses in figure, is established in a strip of copper of height h and width w. A uniform field of magnetic induction B is applied at right angle to the strip.
(a) Calculate the drift velocity vd of the electrons.
(b) What are the magnitude and direction of the magnetic force F acting on the electrons?
(c) What should the magnitude and direction of a homogeneous electric field E be in order to counterbalance the effect of mangetic field?
(d) Calculate voltage V necessary between two sides of the conductor in order to creat this field E Between which sides of the conductor would this voltage have to be applied?
(e) If no electric field is applied from the outside, the electrons will be pushed somewhat to one side and therefore will give rise to a uniform electric field EH across the conductor until the forces of this electrostatic field EH balance the magnetic forces encountered in part (b). What will be the magnitude and direction of field EH?
Assume that n, the number of conductor electrons per unit volume is 1.1×1029m−3,h=0.02m,w=0.1cm,i=50A,andB=2T.

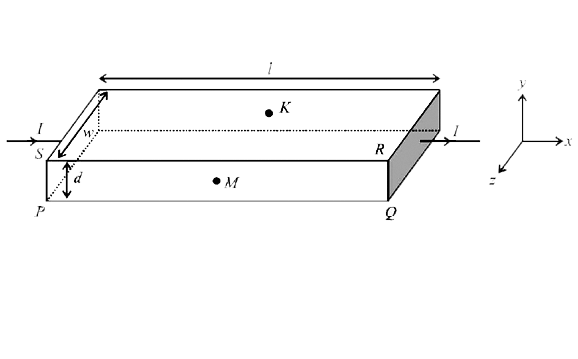
View SolutionIn a thin rectangular metallic strip a constant current I flows along the positive x-direction , as shown in the figure. The length , width and thickness of the strip are l,wandd, respectively.
A uniform magnetic field →B is applied on the strip along the positive y−direction . Due to this, the charge carriers experience a net deflection along the z−direction . This results in accumulation of charge carriers on the surface PQRS ansd apperance of equal and opposite charges on the face opposite to PQRS. A potential difference along the z−direction is thus developed. Charge accumulation contiues untill the magnetic force is balanced by the electric force. The current is assumed to be uniformly distributed on the cross- section of the strip and carried by electrons.
Consider two different metallic strips (1and2) of same dimensions n1andn2, repectrively . Strip 1 is placed in magnetic field B1 and strip 2 is placed in magnetic field B2 , both along positive y−directions. Then V1andV2 are the potential differences developed between KandM in strips 1 and 2 , respectively . Assuming that the current I is the same for both the strips, the correct option(s) is (are)

View SolutionIn a thin rectangular metallic strip a constant current I flows along the positive x-direction , as shown in the figure. The length , width and thickness of the strip are l,wandd, respectively.
A uniform magnetic field →B is applied on the strip along the positive y−direction . Due to this, the charge carriers experience a net deflection along the z−direction . This results in accumulation of charge carriers on the surface PQRS ansd apperance of equal and opposite charges on the face opposite to PQRS. A potential difference along the z−direction is thus developed. Charge accumulation contiues untill the magnetic force is balanced by the electric force. The current is assumed to be uniformly distributed on the cross- section of the strip and carried by electrons.
Consider two different metallic strips (1and2) of same dimensions n1andn2, repectrively . Strip 1 is placed in magnetic field B1 and strip 2 is placed in magnetic field B2 , both along positive y−directions. Then V1andV2 are the potential differences developed between KandM in strips 1 and 2 , respectively . Assuming that the current I is the same for both the strips, the correct option(s) is (are)

View Solution
