If the radius of outside cylinder is η times the inside one for a cable consisting of two thin walled co- axial metallic cylinders, the inductance per unit length is
The correct Answer is:A, B
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - MOTIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-3 (LEVEL-II)
3 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MOTIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-4 (LEVEL-I)
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MOTIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-2 (LEVEL-II)
2 Videos
- ELECTRO MAGNETIC WAVES BOOK - MOTIONCHAPTER - ELECTRO MAGNETIC WAVES EXERCISE - EXERCISE - 3 (SECTION - B)
8 Videos
- ELECTROMAGNETISMBOOK - MOTIONCHAPTER - ELECTROMAGNETISMEXERCISE - Exercise
136 Videos
Similar Questions
Find the self inductance of a unit length of a cable consisting of two thin walled coaxial metallic cylinders if the radius of the outside cylinder is η(η>1) times that of the inside one. The permeability of the medium between the cylinders is assumed to be equal to unity.
View SolutionFind the inductance of a unit length of a cable consisting of two thin-walled coaxial metallic cylinders if the radius of the outside cylinder is η=3.6 times that of the inside one. The permeabitity of a medium between the cylinders is assumed to be equal to unity.
View Solution
Knowledge Check
A current of I ampere flows along an infinitely long straight thin walled hollow metallic cylinder of radius r. The magnetic field at any point inside the cylinder at a distance x from the axis of the cylinder is
A∞Bμ0I2πrCμ0I2πxDzeroA long straight cable of length l is placed symmetrically along z-axis and has radius a(<<l). The cable consists of a thin wire and a co- axial conducting tube. An alternating current I(t)=I0 sin (2πvt). Flows down the central thin wire and returns along the co-axial conducting tube. the induced electric at a distance s from the wire inside the cable is
E(s,t)=μ0I0v cos (2πvt)In(sa)ˆk.
(i) Calculate the displacement current density inside the cable.
(ii) Integrate the displacement current density across the cross- section of the cable to find the total displacement current Id.
(iii) compare the conduction current I0 with the displacement current Id0.A2πλ2I0ln(as)sin(2πυt)ˆkB1λ2I0ln(as)sin(2πυt)ˆkCπλ2I0ln(as)sin(2πυt)ˆkDZero
A long, straight wire is surrounded by a hollow metal cylinder whose axis coincides with that of the wire. The wire has a charge per unit length of λ, and the cylinder has a net charge per unit length of 2λ. From this information, use Gauss's law to find (i) the charge per unit length on the inner and outer surfaces of the cylinder and (ii) the electric field outside the cylinder, a distance r from the axis.
View SolutionA long, straight wire is surrounded by a hollow metal cylinder whose axis coincides with that of the wire. The wire has a charge per unit length of λ, and the cylinder has a net charge per unit length of 2λ. From this information, use Gauss's law to find (i) the charge per unit length on the inner and outer surfaces of the cylinder and (ii) the electric field outside the cylinder, a distance r from the axis.
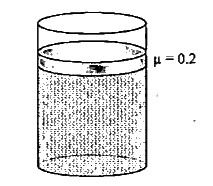
View SolutionFigure-2.47 shows a cylindrical container of radius 5cm and a piston is fitted in it to enclose a length of 20 cm in it.The cylinder contains an ideal gas at a pressure of 1 atmosphere and 300 K temperature.The cylinder is slowly heated and it is found that the piston starts displacing when the gas temperature reaches 600 K. It is given that the friction coefficient between the piston sidesand the container wall is 0.2. Find the normal force acting between piston sides and the container wall per unit length ofits circumference.
View SolutionFind the inductane of a unit length of a double line if the radius of each wire is η times less than the distance between the axes of the wires. The field inside the wires is to be neglected, the permeability is assumed to be equal to unity throughout, and η>>1.
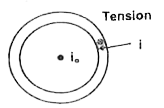
View SolutionA long thin walled hollow cylinder of radius r is carrying a current I. A very long current carrying straight conductor is passing through the axis of the hollow cylinder, carrying a current i0. Find the tension per unit length developed in the hollow cylinder due to the interaction of the straight current carrying conductor.
View SolutionA long straight cable of length l is placed symmetrically along z-axis and has radius a(<<l). The cable consists of a thin wire and a co- axial conducting tube. An alternating current I(t)=I0 sin (2πvt). Flows down the central thin wire and returns along the co-axial conducting tube. the induced electric at a distance s from the wire inside the cable is
E(s,t)=μ0I0v cos (2πvt)In(sa)ˆk.
(i) Calculate the displacement current density inside the cable.
(ii) Integrate the displacement current density across the cross- section of the cable to find the total displacement current Id.
(iii) compare the conduction current I0 with the displacement current Id0.
View Solution
