If three electric di-poles are placed in some closed surface, then the electric flux emitting from the surface will be -
zero
positive
negative
None
The correct Answer is:A
To solve the problem of determining the electric flux emitting from a closed surface containing three electric dipoles, we can follow these steps:
1. Understanding Electric Dipoles:
An electric dipole consists of two equal and opposite charges separated by a distance. For example, if we have a dipole with charges +q and -q, the net charge of the dipole is zero.
2. Identifying the Closed Surface:
We are given that three electric dipoles are placed within a closed surface. This closed surface can be treated as a Gaussian surface for the application of Gauss's law.
3. Applying Gauss's Law:
Gauss's law states that the electric flux (Φ) through a closed surface is equal to the total charge (Q) enclosed by that surface divided by the permittivity of free space (ε₀):
Φ=Qenclosedε0
4. Calculating the Enclosed Charge:
Since each dipole consists of a positive and a negative charge, the net charge of each dipole is zero. Therefore, for three dipoles:
- Dipole 1: +q and -q → Net charge = 0
- Dipole 2: +q and -q → Net charge = 0
- Dipole 3: +q and -q → Net charge = 0
Thus, the total charge enclosed by the closed surface is:
Qenclosed=0+0+0=0
5. Finding the Electric Flux:
Substituting the enclosed charge into Gauss's law:
Φ=0ε0=0
6. Conclusion:
The electric flux emitting from the closed surface containing the three dipoles is zero.
Final Answer:
The electric flux emitting from the surface will be 0.
---
An electric dipole consists of two equal and opposite charges separated by a distance. For example, if we have a dipole with charges +q and -q, the net charge of the dipole is zero.
We are given that three electric dipoles are placed within a closed surface. This closed surface can be treated as a Gaussian surface for the application of Gauss's law.
Gauss's law states that the electric flux (Φ) through a closed surface is equal to the total charge (Q) enclosed by that surface divided by the permittivity of free space (ε₀):
Φ=Qenclosedε0
Since each dipole consists of a positive and a negative charge, the net charge of each dipole is zero. Therefore, for three dipoles:
- Dipole 1: +q and -q → Net charge = 0
- Dipole 2: +q and -q → Net charge = 0
- Dipole 3: +q and -q → Net charge = 0
Thus, the total charge enclosed by the closed surface is:
Qenclosed=0+0+0=0
Substituting the enclosed charge into Gauss's law:
Φ=0ε0=0
The electric flux emitting from the closed surface containing the three dipoles is zero.
The electric flux emitting from the surface will be 0.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - MOTIONCHAPTER - ELECTROSTATICSEXERCISE - Exercise - 2 (Objective Problems | NEET)
64 Videos
- ELECTROSTATICSBOOK - MOTIONCHAPTER - ELECTROSTATICSEXERCISE - Exercise -3 Section (A)
41 Videos
- ELECTROSTATICSBOOK - MOTIONCHAPTER - ELECTROSTATICSEXERCISE - SELF PRACTICE PROBLEM
27 Videos
- ELECTRONICS - SEMI CONDUCTORBOOK - MOTIONCHAPTER - ELECTRONICS - SEMI CONDUCTOREXERCISE - EXERCISE - 3
29 Videos
- ELECTROSTATICS - I BOOK - MOTIONCHAPTER - ELECTROSTATICS - I EXERCISE - EXERCISE - 4 (Level -II) PREVIOUS YEAR - JEE ADVANCED
13 Videos
Similar Questions
Knowledge Check
The electric flux through the surface
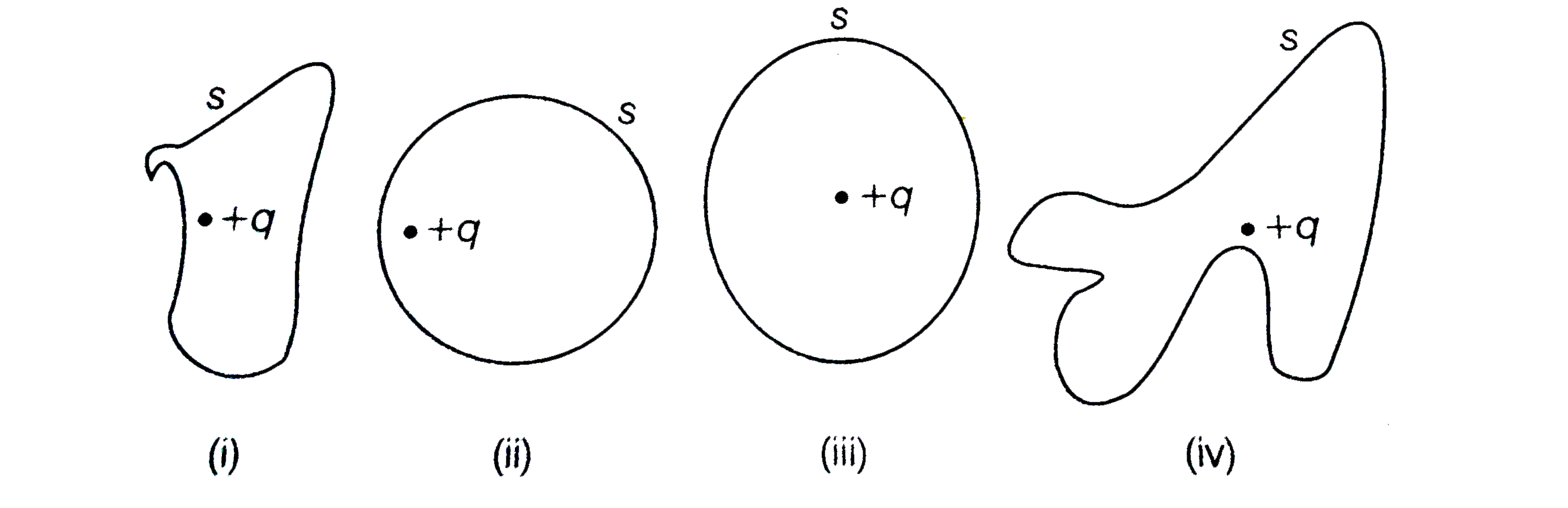 Ain fig. (iv) is the largestBin fig. (iii) is the leastCin fig. (ii) is same as fig.(iii) but is smaller than fig.(iv)DIs the same for all the figures.
Ain fig. (iv) is the largestBin fig. (iii) is the leastCin fig. (ii) is same as fig.(iii) but is smaller than fig.(iv)DIs the same for all the figures.The electric flux through the surface
 Ain fig, (iv) is the largestBin fig, (iii) is the leastCin fig (ii) is same as a fig (iii) but is smaller than that in Fig (iv).Dis the same for all the figures.
Ain fig, (iv) is the largestBin fig, (iii) is the leastCin fig (ii) is same as a fig (iii) but is smaller than that in Fig (iv).Dis the same for all the figures.If the net electric field flux passing through a closed surface is zero, then the electric field at the surface will be
A0Bsame at all placesCdepends upon the location of pointsDinfinite
Electric Flux And Equipotential Surface
View SolutionIf a spherical conductor comes out from the closed surface of the sphere then total flux emitted from the surface will be
View SolutionWhat is the electric flux linked with closed surface?
View SolutionA surface enclosed an electric dipole, the flux through the surface is -
View SolutionIf the net electric flux through a closed surface is zero, then we can infer
View Solution