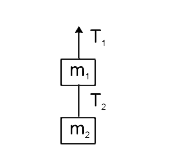
Two blocks with masses kg and kg hang one under other as shown in figure. Find the tensions in the strings (massless) in the following situations :
if maximum allowable tension is 10 N. What is maximum possible upward acceleration ?
The correct Answer is:
To solve the problem of finding the tensions in the strings and the maximum possible upward acceleration, we will follow these steps:
Step 1: Identify the Forces Acting on Each Block
We have two blocks:
- Block 1 (mass m1=0.2 kg)
- Block 2 (mass m2=0.3 kg)
The forces acting on each block are:
- For Block 1:
- Weight W1=m1⋅g=0.2⋅10=2 N (acting downwards)
- Tension T1 (acting upwards)
- For Block 2:
- Weight W2=m2⋅g=0.3⋅10=3 N (acting downwards)
- Tension T2 (acting upwards)
Step 2: Write the Equations of Motion
Assuming both blocks are accelerating upwards with acceleration a:
1. For Block 1:
T1−W1=m1⋅a⟹T1−2=0.2a(1)
2. For Block 2:
T2−W2=m2⋅a⟹T2−3=0.3a(2)
Step 3: Relate the Tensions
Since Block 1 is above Block 2, the tension in the string supporting Block 1 must be greater than the tension in the string supporting Block 2:
T1=T2+W1(3)
Step 4: Substitute T1 in Terms of T2
From equation (3), we can express T1 in terms of T2:
T1=T2+2
Step 5: Substitute T1 into Equation (1)
Substituting T1 from equation (3) into equation (1):
(T2+2)−2=0.2a
This simplifies to:
T2=0.2a(4)
Step 6: Substitute T2 into Equation (2)
Now substituting T2 from equation (4) into equation (2):
0.2a−3=0.3a
Rearranging gives:
−3=0.3a−0.2a⟹−3=0.1a⟹a=−30 m/s2
This negative acceleration indicates that our assumption of upward acceleration is incorrect.
Step 7: Find the Maximum Allowable Tension
Given that the maximum allowable tension is 10 N, we can set T1=10 N:
10−2=0.2a⟹8=0.2a⟹a=40 m/s2
Step 8: Conclusion
The maximum possible upward acceleration is 40 m/s2.
We have two blocks:
- Block 1 (mass m1=0.2 kg)
- Block 2 (mass m2=0.3 kg)
- For Block 1:
- Weight W1=m1⋅g=0.2⋅10=2 N (acting downwards)
- Tension T1 (acting upwards)
- For Block 2:
- Weight W2=m2⋅g=0.3⋅10=3 N (acting downwards)
- Tension T2 (acting upwards)
Assuming both blocks are accelerating upwards with acceleration a:
1. For Block 1:
T1−W1=m1⋅a⟹T1−2=0.2a(1)
T2−W2=m2⋅a⟹T2−3=0.3a(2)
Since Block 1 is above Block 2, the tension in the string supporting Block 1 must be greater than the tension in the string supporting Block 2:
T1=T2+W1(3)
From equation (3), we can express T1 in terms of T2:
T1=T2+2
Substituting T1 from equation (3) into equation (1):
(T2+2)−2=0.2a
This simplifies to:
T2=0.2a(4)
Now substituting T2 from equation (4) into equation (2):
0.2a−3=0.3a
Rearranging gives:
−3=0.3a−0.2a⟹−3=0.1a⟹a=−30 m/s2
This negative acceleration indicates that our assumption of upward acceleration is incorrect.
Given that the maximum allowable tension is 10 N, we can set T1=10 N:
10−2=0.2a⟹8=0.2a⟹a=40 m/s2
The maximum possible upward acceleration is 40 m/s2.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION & FRICTION BOOK - MOTIONCHAPTER - NEWTON'S LAWS OF MOTION & FRICTION EXERCISE - Questions For Practice
25 Videos
- NEWTON'S LAWS OF MOTION & FRICTION BOOK - MOTIONCHAPTER - NEWTON'S LAWS OF MOTION & FRICTION EXERCISE - Exercise - 1 (SECTION-A:- String Constrained, Wedge Constrained, Newtons Law theory Question, Equillibrium Questions (Normal and Tension), Problems with Acceleration (F=ma), Wedge problems)
27 Videos
- NEWTON'S LAWS OF MOTION & FRICTION BOOK - MOTIONCHAPTER - NEWTON'S LAWS OF MOTION & FRICTION EXERCISE - Exercise - 3 Section-B
12 Videos
- MODERN PHYSICS -1BOOK - MOTIONCHAPTER - MODERN PHYSICS -1EXERCISE - EXERCISE-4 ( LEVEL- II)
39 Videos
- NLM & FRICTIONBOOK - MOTIONCHAPTER - NLM & FRICTIONEXERCISE - EXERCISE-4 ( LEVEL-II)
15 Videos
Similar Questions
Two blocks with masses m1=0.2 kg and m2=0.3 kg hang one under other as shown in figure. Find the tensions in the strings (massless) in the following situations :
(g=10m/s2)
the blocks are at rest
View SolutionTwo blocks with masses m1=0.2 kg and m2=0.3 kg hang one under other as shown in figure. Find the tensions in the strings (massless) in the following situations :
(g=10m/s2)
they move upward at 5 m/s
View Solution
Knowledge Check
Two blocks of masses mi=2kg and m2=4kg hang, over a massless pulley as shown in the figure. A force F0=100N acting at the axis of the pulley accelerates the system upwards Then :
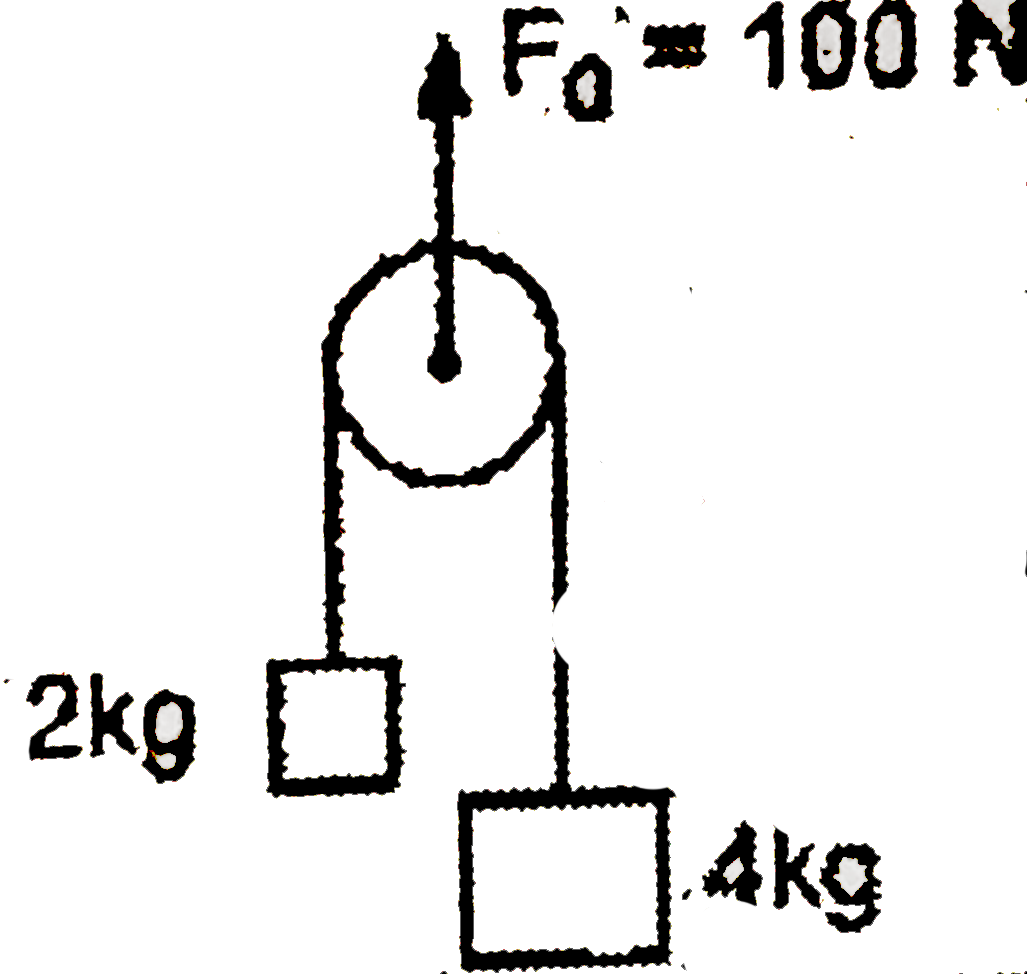 Aacceleration of 2kg mass is 15m/s2Bacceleration of 4kg mass is 2.5m/s2Cacceleration of both masses is sameDacceleration of both the masses is upward
Aacceleration of 2kg mass is 15m/s2Bacceleration of 4kg mass is 2.5m/s2Cacceleration of both masses is sameDacceleration of both the masses is upwardThree blocks A,B and C of mass 10 kg each are hanging on a string passing over a fixed frictionless pulley as shown in figure. The tension in the string connecting blocks B and C is (g=10m/s2)
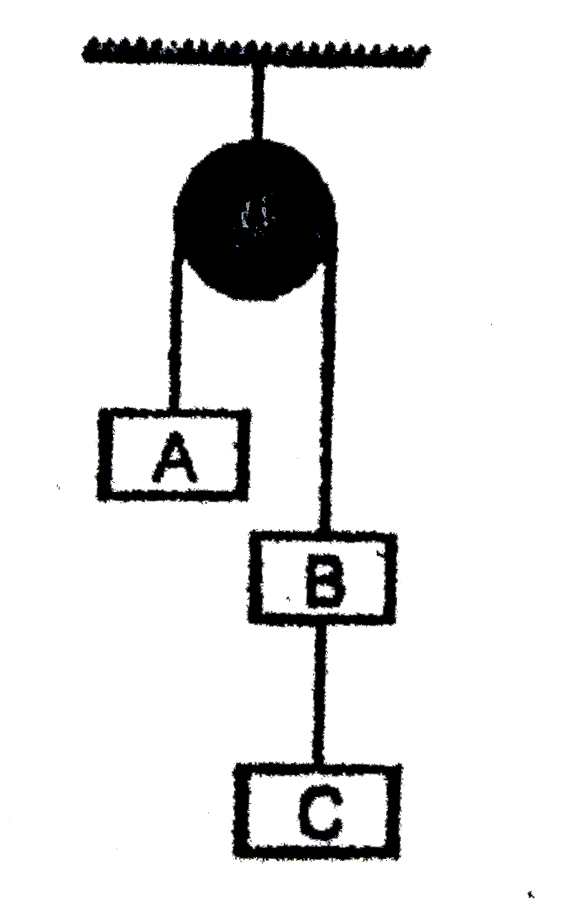 A20003NB4003NC100 ND2003N
A20003NB4003NC100 ND2003NTwo blocks of masses m1=2kg and m2=5kg hang over a massless pulley as shown in the figure. A force F0=100N acting at the axis of the pulley accelerates the system upwards. Then :( Take g=9.8m/s2)
 AAcceleration of 2kg mass is 15.2m/sec2BAcceleration of 5kg mass is 0.2m/sec2CAcceleration of both the masses is sameDAcceleration of both the masses is upward
AAcceleration of 2kg mass is 15.2m/sec2BAcceleration of 5kg mass is 0.2m/sec2CAcceleration of both the masses is sameDAcceleration of both the masses is upward
Two blocks with masses m1=0.2 kg and m2=0.3 kghang one under other as shown in figure. Find the tensions in the strings (massless) in the following situations :
(g=10m/s2)
they accelerate upward at 2m/s2
View SolutionTwo blocks with masses m1=0.2 kg and m2=0.3 kg hang one under other as shown in figure. Find the tensions in the strings (massless) in the following situations :
(g=10m/s2)
they accelerate downward at 2m/s2
View SolutionA 'block' of mass 10 kg is suspended with string as shown in figure. Find tension in the string. (g=10m/s2)

View SolutionIn the situation shown, the tension in the string is 22N. What is m (in kg) ?
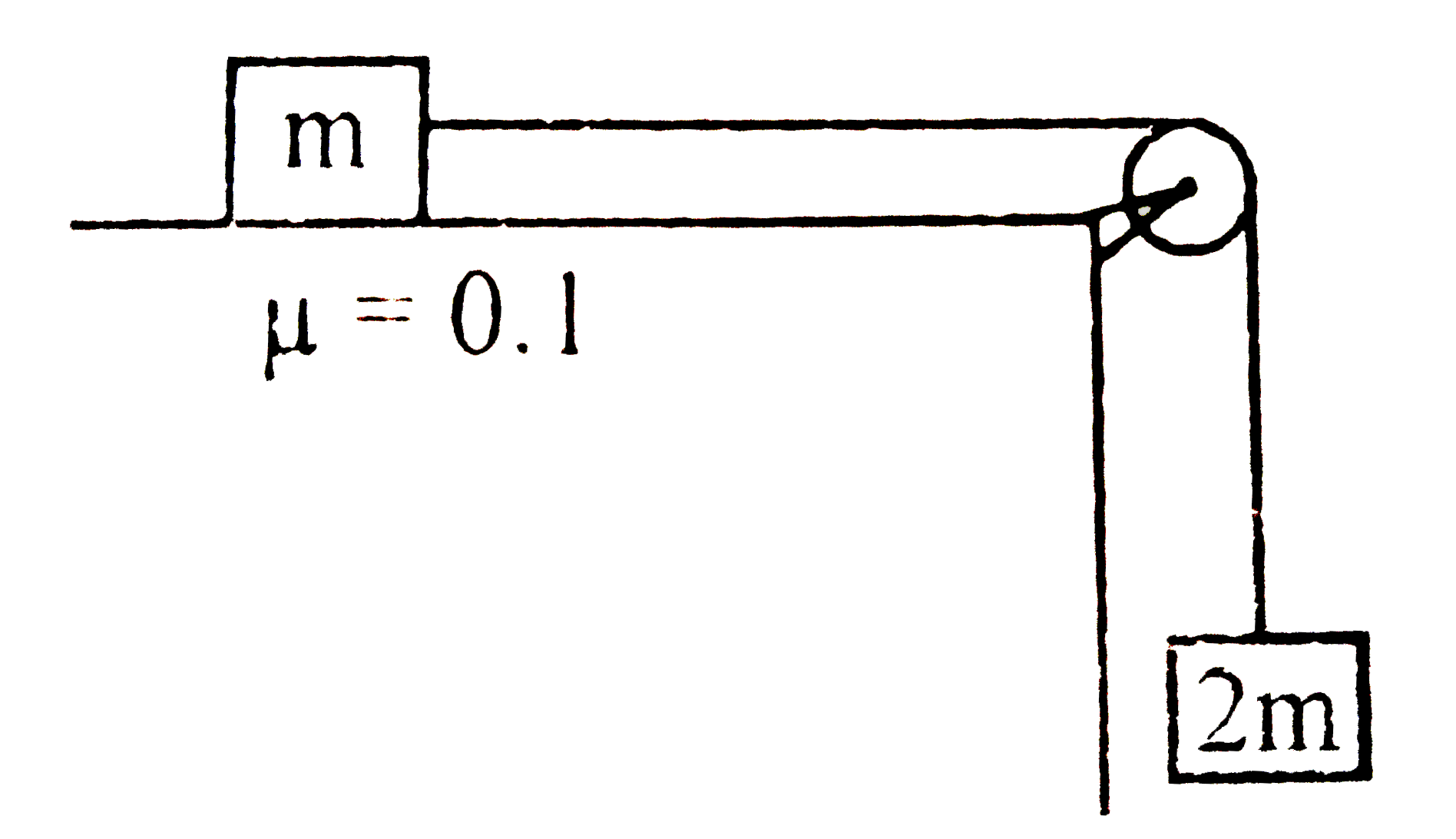
View SolutionTwo masses m1 and m2 are connected by a massless string as shown in Fig. Find the value of tension in the string if a force of 200 N is applied on (i) m1 and m2.

View Solution
