It is given that . Is it true to say that and ? Why?
To determine whether the statements ∠D=∠R and ∠F=∠P are true, we will analyze the properties of similar triangles.
1. Understanding Similar Triangles:
We are given that triangle DEF is similar to triangle RPQ, denoted as ΔDEF~ΔRPQ. This means that the corresponding angles of these triangles are equal, and the sides are in proportion.
Hint: Recall the definition of similar triangles and the properties that come with them.
2. Identifying Corresponding Angles:
From the similarity of the triangles, we can identify the corresponding angles:
- Angle D corresponds to angle R.
- Angle E corresponds to angle P.
- Angle F corresponds to angle Q.
Hint: Make a list of the corresponding angles based on the order of the vertices in the triangle notation.
3. Writing the Equalities:
Based on the correspondence, we can write:
- Angle D = Angle R
- Angle E = Angle P
- Angle F = Angle Q
Hint: Use the property of corresponding angles to establish these equalities.
4. Analyzing the Given Statements:
The question asks if ∠D=∠R and ∠F=∠P are true.
- We have established that angle D = angle R, which is true.
- However, angle F corresponds to angle Q, not angle P. Therefore, angle F = angle P is false.
Hint: Check each statement against the established correspondences.
5. Conclusion:
The statement ∠D=∠R is true, but the statement ∠F=∠P is false. Therefore, the overall conclusion is that the statement as a whole is not true.
Hint: Summarize your findings clearly to conclude the analysis.
Final Answer:
- Angle D = Angle R (True)
- Angle F = Angle P (False)
- Overall conclusion: The statement is false.
We are given that triangle DEF is similar to triangle RPQ, denoted as ΔDEF~ΔRPQ. This means that the corresponding angles of these triangles are equal, and the sides are in proportion.
From the similarity of the triangles, we can identify the corresponding angles:
- Angle D corresponds to angle R.
- Angle E corresponds to angle P.
- Angle F corresponds to angle Q.
Based on the correspondence, we can write:
- Angle D = Angle R
- Angle E = Angle P
- Angle F = Angle Q
The question asks if ∠D=∠R and ∠F=∠P are true.
- We have established that angle D = angle R, which is true.
- However, angle F corresponds to angle Q, not angle P. Therefore, angle F = angle P is false.
The statement ∠D=∠R is true, but the statement ∠F=∠P is false. Therefore, the overall conclusion is that the statement as a whole is not true.
- Angle D = Angle R (True)
- Angle F = Angle P (False)
- Overall conclusion: The statement is false.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
In ΔDEFandΔPQR, it is given that ∠D=∠Qand∠R=∠E, then which of the following is not true?
AEFPR=DFPQBDEPQ=EFRPCDEQR=DFPQDEFRP=DEQR - Question 2 - Select One
It is given that ΔABC≅ΔFDE and AB= 5 cm , ∠B=40∘ and ∠A=80∘ then which of the following is true ?
ADF=5cm,∠F=60∘BDF=5cm,∠E=60∘CDE=5cm,∠E=60∘DDE=5cm,∠D=60∘ - Question 3 - Select One
If ΔPQR~ΔDEF,∠P=65∘and∠F=32∘, then ∠Q is
A32∘B65∘C83∘D97∘
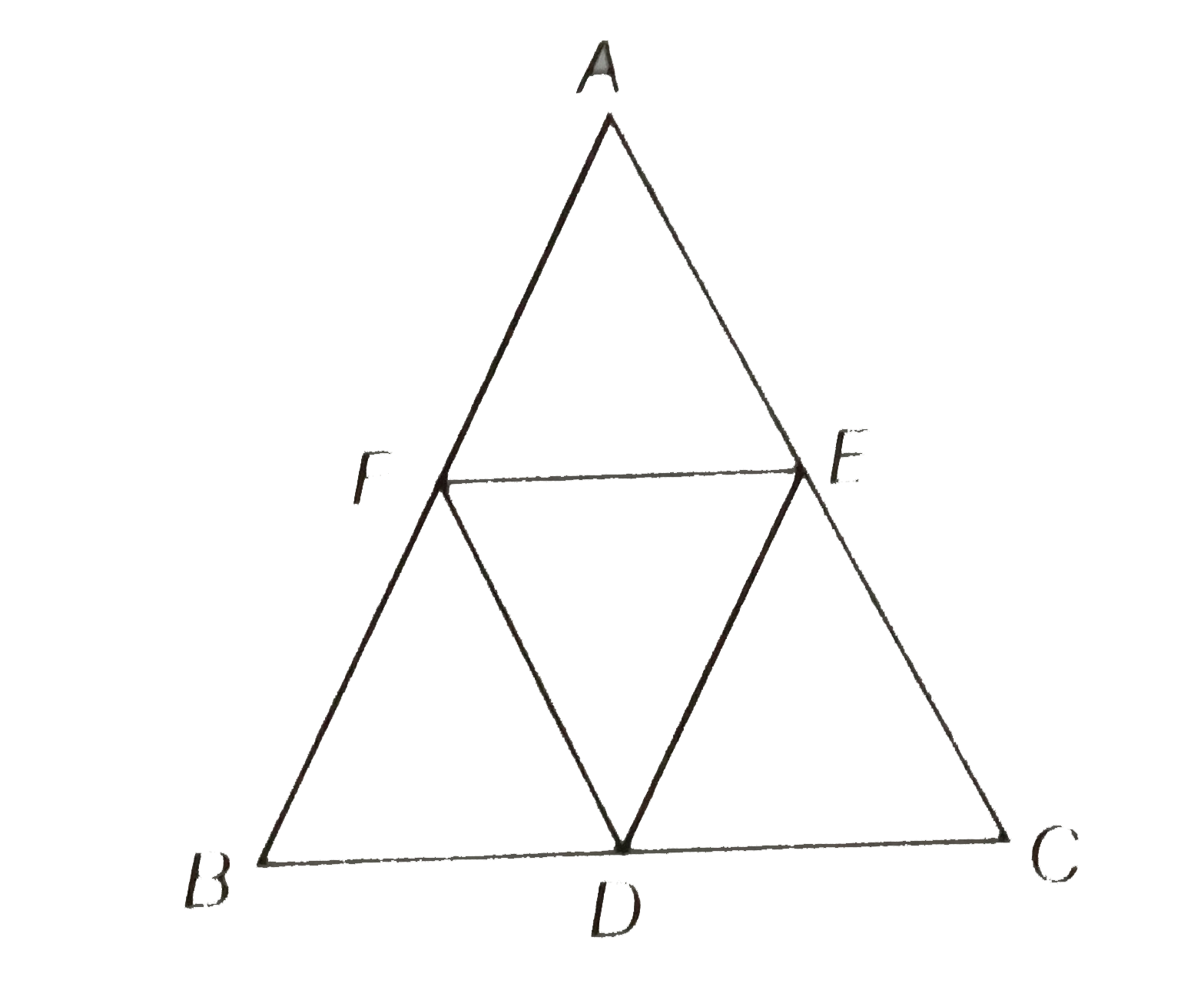
In the figure, it is given that BDEF and FDCE are parallelogram. Can you say that BD = CD ? Why or why not?
 View Solution
View SolutionWhich of the following pairs of triangles are congruent ? Also state the condition of congruency in each case :

(iv) In ΔABC and ΔDEF,AB=EF,BC=DF and ∠B=∠F
(v) In ΔABC and ΔPQR,AB=QR,AC=PR and ∠B=∠R
(vi) In ΔABC and ΔPQR,∠A=∠P,AC=PR and AB=PQ
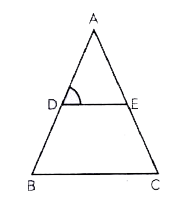
(vi) In ΔABC and ΔPQR,AB=QR,∠A=∠Q and AC=QP.View SolutionIn the given figure, if ∠D=∠C, then it is true that △ADE~△ACB? Why?
 View Solution
View SolutionIn ΔABCandΔDEF, it is given that ∠B=∠Eand∠C=∠F, In order that ΔABC≅ΔDEF, we must have
View SolutionConstruct the incircle of a given triangle ABC. The following sentences are the steps involved in the above construction. Arrange them in sequencial order from first to left.
(A) Draw perpendicular ¯¯¯¯¯¯IM from I onto ¯¯¯¯¯¯BC.
(B) Taking I as centre and IM as the radius , draw a circle.
(C) Draw a DABC with the given measurements.
(D) Draw bisects of two to the angles. say ∠Band∠C to intersect at I.
(D) Draw bisects of two of the angles, say ∠Band∠C to intersect at I.View Solution

