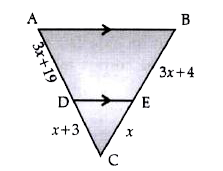
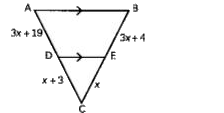
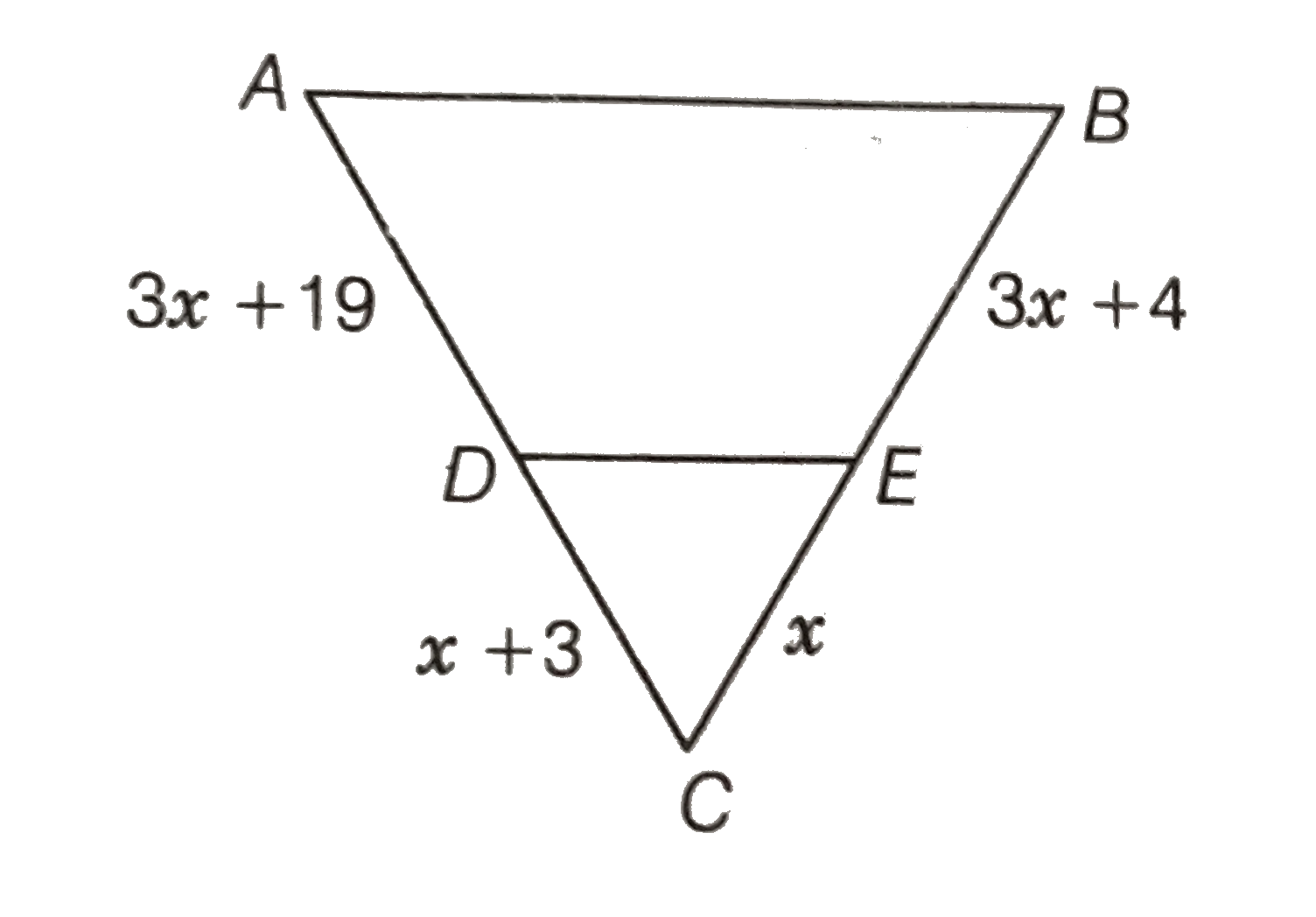
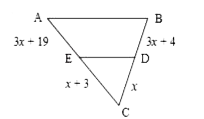
Find the value of x for which DE||AB in given figure.
A
1
B
3
C
4
D
2
Video Solution
Text Solution
The correct Answer is:D
Given, DE||AB
∴CDAD=CEBE [by basic proportionality theorem]
⇒x+33x+19=x3x+4
⇒(x+3)(3x+4)=x(3x+19)
⇒3x2+4x+9x+12=3x2+19x
⇒19x−13x=12
⇒6x=12
∴x=126=2
Hence, the required value of x is 2.

|
Topper's Solved these Questions
Similar Questions
Knowledge Check
What value of x will make DE || AB in the given figure?
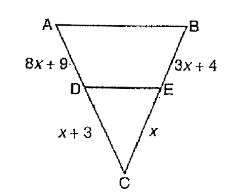 Ax = 3Bx = 2Cx = 1Dx = 5
Ax = 3Bx = 2Cx = 1Dx = 5In the given figure, AB∣∣CD,∠ABO=40∘,∠CDO=35∘. Find the value of the reflex ∠BOD and hence the value of x.
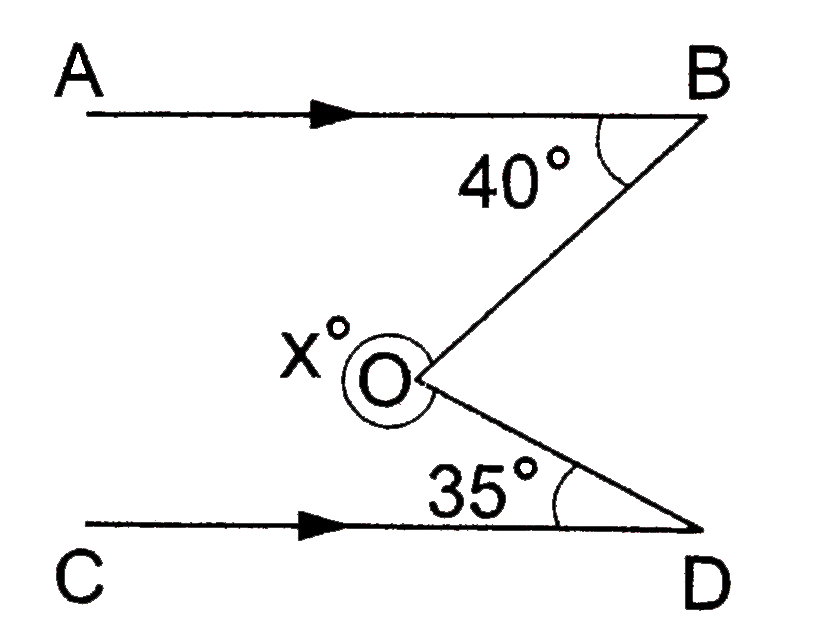 A283B284C285D286
A283B284C285D286
Evaluate for x, if, AB∣∣DC in the given figure.
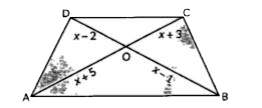
View SolutionFind the value of x in the given figure AB∣∣CD
View SolutionIn the given figure, if DE || AC , then AB =
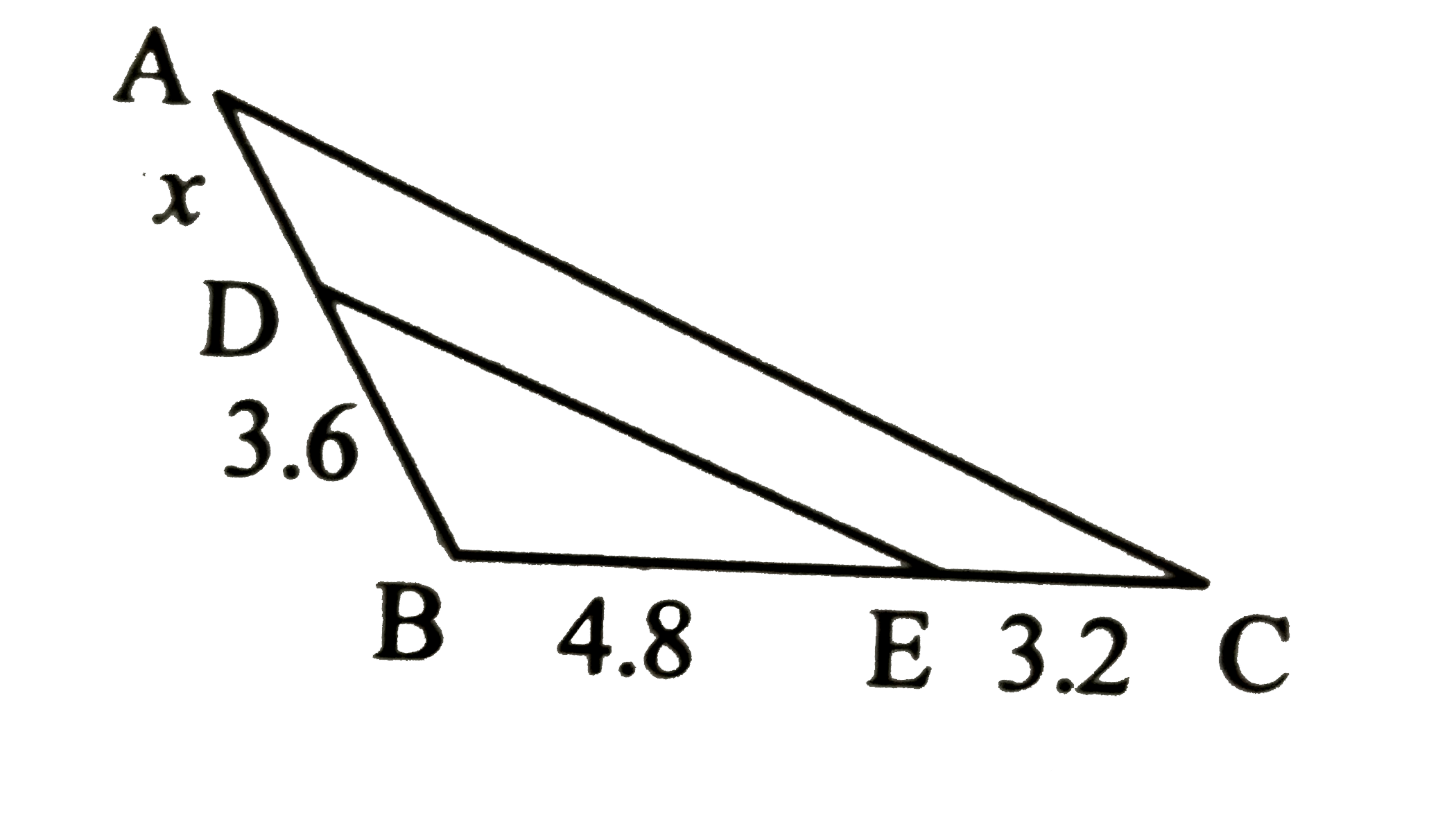
View SolutionIn Figure, find the values of x and y and then show that AB∣∣CD
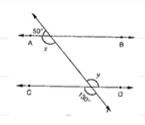
View SolutionIn the given figure, find the value of x which will make DE||AB ?
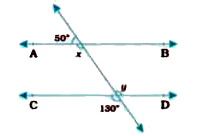
View SolutionIn the given figure, find the values of x and y and then show that AB∣∣CD.
View Solution