In $P Q R, Q M ⊥ P R$ and $P R^{2} - P Q^{2} = Q R^{2}$ .Prove that $Q M^{2} = P M \times M R$

Video Solution

Text Solution

Verified by Experts

Given in $Δ P Q R$ , $P R^{2} - P Q^{2} = Q R^{2} and Q M ⊥ P R$
To prove $Q M^{2} = P M \times M R$
Proof Since, $P R^{2} - P Q^{2} = Q R^{2}$
$\Rightarrow P R^{2} = P Q^{2} + Q R^{2}$

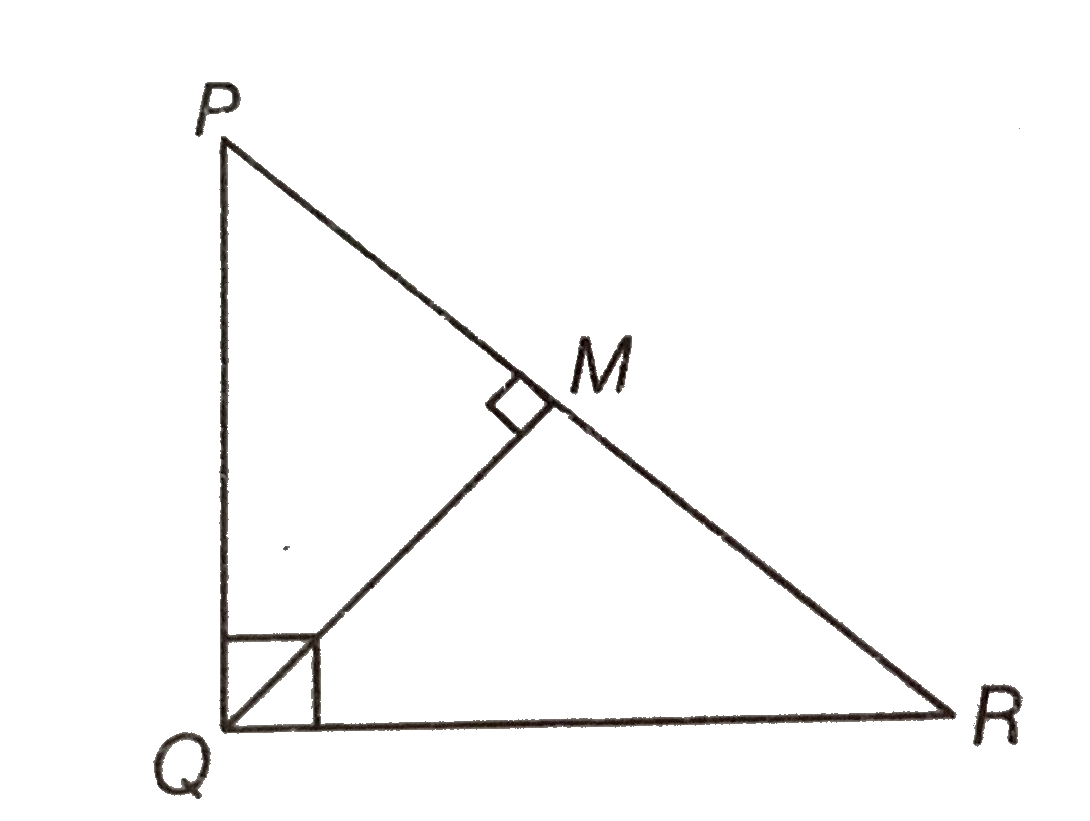
So, $Δ P Q R$ is right angled triangle at Q.
In $Δ P Q R$ iss right angled triangle at Q.
In $Δ Q M R$ and $Δ P M Q$ ,
$∠ M = ∠ M$ [each $90^{\circ}$ ]
$∠ M Q R = ∠ Q P M$ [each equal to $90^{\circ} -' ∠ R$ ]
$Δ Q M R ~ Δ P M Q$ [by AAA similarity criterion]
Now, using property of area of similar triangles, we get
$\frac{a r (Δ Q M R)}{a r (Δ P M Q)} = \frac{{(Q M)}^{2}}{{(P M)}^{2}}$
$\Rightarrow \frac{\frac{1}{2} \times R M \times Q M}{\frac{1}{2} \times P M \times Q M} = \frac{{(Q M)}^{2}}{{(P M)}^{2}}$ [ $∵$ areaa of triangle= $\frac{1}{2} \times$ base $\times$ height]
$\Rightarrow Q M^{2} = P M \times R M$ Hence proved.

Updated on:21/07/2023