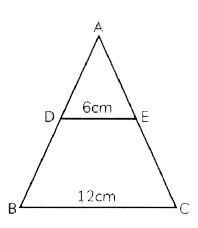
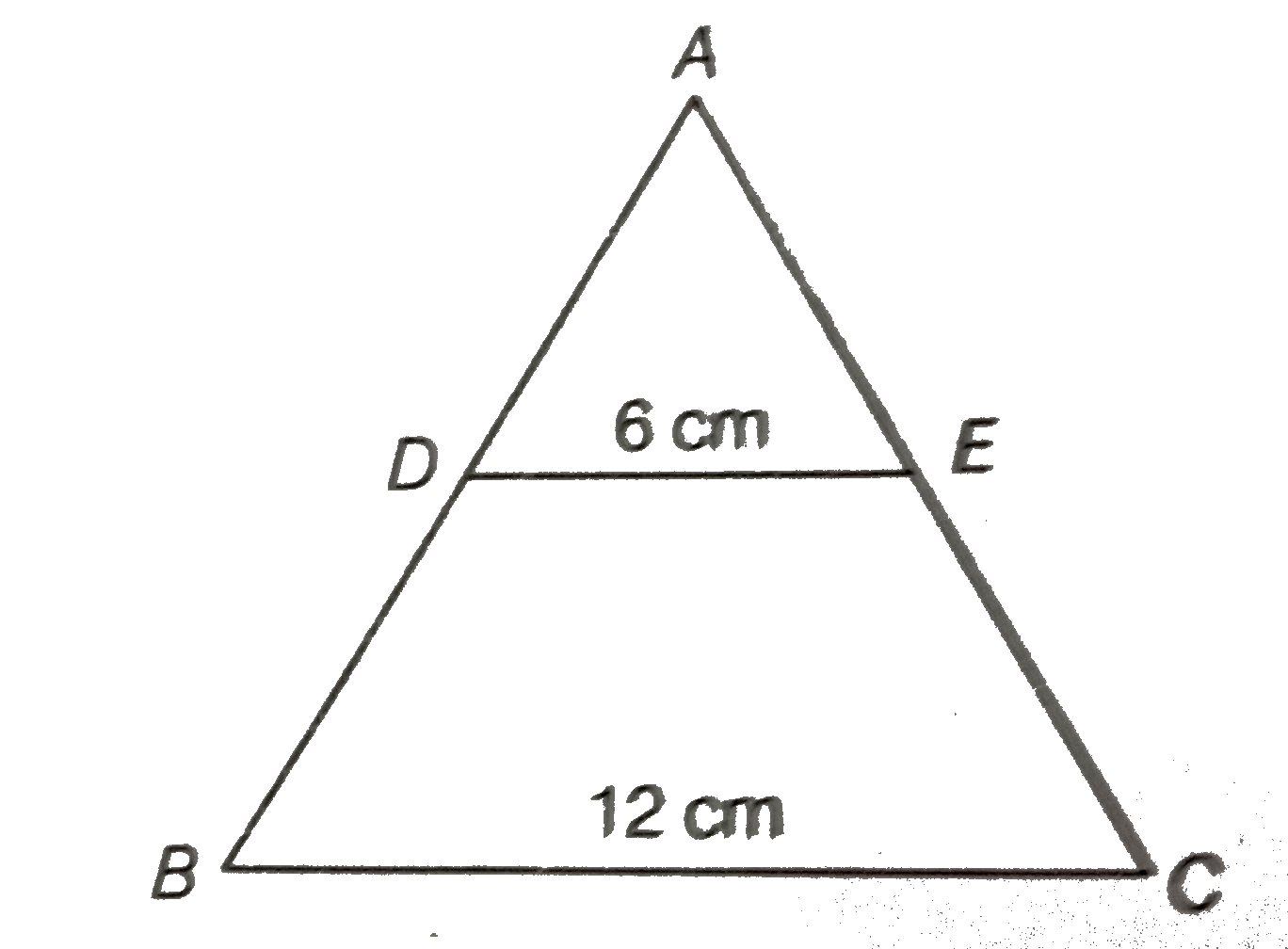
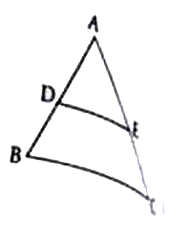
In figure, if DE||BC, then find the ratio of ar (ΔADE) and ar(DECB).
A
1:3
B
1:2
C
2:5
D
3:5
Video Solution
Text Solution
The correct Answer is:A
Given, DE||BC, DE= 6 cm and BC= 12 cm
In ΔADE,
∠ABC=∠(ADE) [corresponding angle]
∠ACB=∠AED [corresponding angle]
and ∠A=∠A [common sides]
∴ΔABC~ΔAED [by AAA similarity criterion]
Then, ar(ΔADE)ar(ΔABC)=(DE)2(BC)2
=(6)2(12)2=(12)2
⇒ar(ΔADE)ar(ΔABC)=(12)2=14
Let ar(ΔADE)=k,then ar(ΔABC)=4k
Now, ar(DECB)=ar(ABC)-ar(ADE)=4k-k=3k
∴ Required ratio=ar(ADE) : ar(DECB)=K : 3k=1 : 3
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure, AD is the median and E is any point on AC, such that ar(ΔMDE) : ar(ΔABD) = 2 : 3, then find the ratio of ar(ΔEDC): ar(ΔABC).
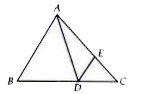 A3 : 4B1 : 6C6 : 1D4 : 3
A3 : 4B1 : 6C6 : 1D4 : 3 - Question 2 - Select One
In the given figure, DE is parallel to BC and the ratio of the areas of ΔADE and trapezium BDEC is 4:5. What is DE: BC?
A1:2B2:3C4:5DNone of these - Question 3 - Select One
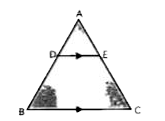
In the adjacent figure DE is parallel to BC and ratio of areas of ΔADE and trapezium BDEC is 4 : 5. What is the value of DE : BC?
 A1:2B2:3C4:5DNone of these
A1:2B2:3C4:5DNone of these
In figure, DE||BC and the ratio of the areas of △ADEand trapezium BDEC is 4:5 . Find the ratio of DE:BC . If BD = 2cm. Then find AD.
View SolutionIn a trapezium ABCD, AB || DC, AB = a cm, and DC = b cm. If M and N are the midpoints of the nonparallel sides, AD and BC respectively then find the ratio of ar(DCNM) and ar(MNBA).
View SolutionIn the figure, DE∣∣BC. If AD=1cm and BD=2cm, then the ratio of areas of ΔADEandΔABC is
 View Solution
View SolutionIn Figure 1, PQ || BC and AP : PB = 1 : 2.find the ratio of arΔAPQarΔABC
View SolutionIn (ΔABC) , MN∣∣BC and AM:AB=13. Then find the ratio of ar(ΔAMN)ar(ΔABC)
View Solution