If a line is drawn to one side of a triangle to intersect the other two sides in distinct points, prove that the other two sides are divided in the same ratio.
Let a ΔABC in which a line DE parallel to BC intersects AB to D and AC at E.
To prove DEE divides the two sides in the same ratio.
i.e., ADDB=AEEC
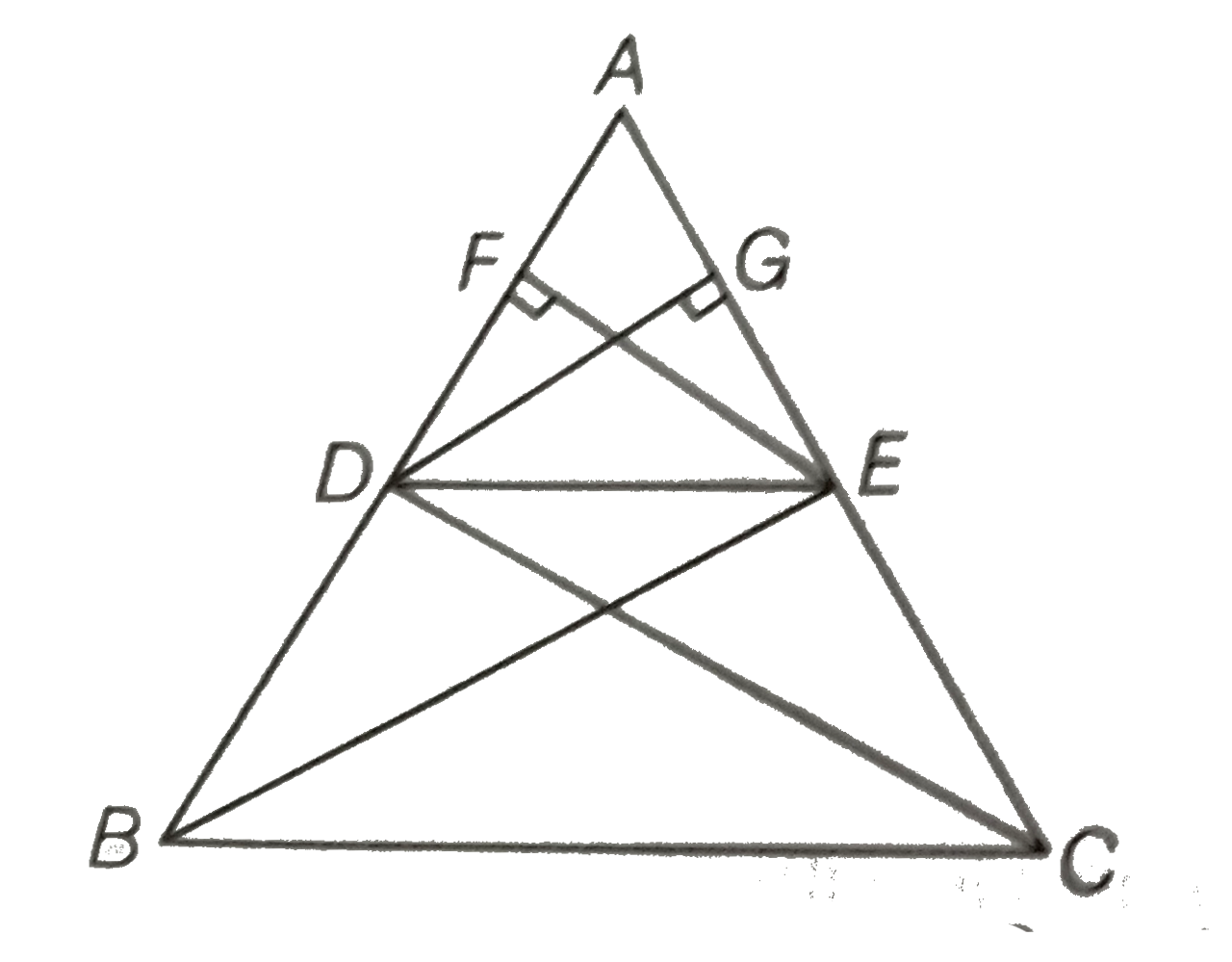
Construction Join BE, CD and draw EF⊥and DG⊥AC.
Proof Here ar(ΔADE)ar(ΔBDE)=12×AD×EF12×DB×EF [∵area of triangle=12×base×height]
=(ADDB)...(i)
similarly, ar(ΔADE)ar(ΔDEC)=12×AE×GD12×EC×GD=AEEC....(ii)
Now since, ΔBDEandΔDEC lie between the same parallel DE and BC and on the same base DE.
So, ar(ΔBDE)=ar(ΔDEC)...(iii)
From Eqs. (i), (ii) and (iii), ADDB=AEEC Hence proved
Topper's Solved these Questions
Similar Questions
Prove that if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then the other two sides are divided in the same ratio.
View SolutionTheorem 6.1 : If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
View Solution
Knowledge Check
- Question 1 - Select One
Thales theorem is given by a greek mathematician. According to this theorem, if a line is drawn parallel to one side of a triangle then it divides the other two sides in the same ratio. This theorem is also known as Basic Proportionality Theorem.
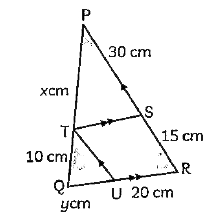
Here, the value of x is :A20 cmB15 cmC5 cmD10 cm
If a line is drawn parallel to one side of a triangle to intersect the other two sides in disinct points, the other two sides are divided in the same ratio. Using this theoure. Find EC in if DE∣∣BC.
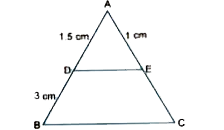 View Solution
View SolutionProve that, if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
Using the above result, do the following:
In Fig. 7 .45 DE||BC and BD = CE. Prove that ΔABC is an isosceles triangle.
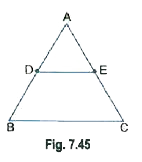 View Solution
View SolutionBasic proportionality Theorem or Thales Theorem - If a line is drawn parallel to one side of a triangle intersecting the other two sides; then it divides the two sides in the same ratio.
View SolutionProve that , "If a line parallel to a side of a triangle intersects the remaining sides in two distinct points then the line divides the sides in the same proportion".
View Solution(B) Solve any two of the following subquestions :
Prove that following statement, " If a line parallel to a side of a Delta intersects the remaining sides in two distinct points , then the line divides the sides in the same proportion . "View SolutionIf a line is drawn parallel to the base of an isosceles triangle to intersect its equal sides, prove that the quadrilateral, so formed is cyclic.
View SolutionIf two sides of a cyclic quadrilateral are equal, prove that the other two sides are parallel.
View Solution

