An aluminium wire of length 0.6 m and cross sectioal are and length 0.866 m .The compound wire is loaded with 10kg.Find the lowest frequency of exciation for which the joint In the the wire.The density of alumimium is 2600 kg m−3 and that of steel is 7800 kgm−3
The correct Answer is:B, C
Step by step video, text & image solution for An aluminium wire of length 0.6 m and cross sectioal are and length 0.866 m .The compound wire is loaded with 10kg.Find the lowest frequency of exciation for which the joint In the the wire.The density of alumimium is 2600 kg m^(-3) and that of steel is 7800 kgm^(-3) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WAVES BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WAVES EXERCISE - Advance MCQs with One or More Options Correct
30 Videos
- WAVE OPTICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WAVE OPTICSEXERCISE - Unsolved Numerical Problems
28 Videos
- X-RAYSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - X-RAYSEXERCISE - Unsolved Numerica Problem for Preparation
23 Videos
Similar Questions
An aluminium wire of length 0.6 m and cross-sectional area 10−6m2 is connected to a steel wire of the same crosssectional area and length 0.866 m. The compound wire is loaded with 10 kg. Find the lowest frequency of excitation for which the joint in the wire is a node. Also find the number ofnodes, excluding the two at the ends of the wire. The density of aluminium is 2600kg/m3 andthatofsteel is 7800kg/m3
View SolutionFigure shows an aluminium wire of length 60 cm joined to a steel wire of length 80 cm and stretched between two fixed supports. The tension produced is 40 N. The cross-sectional area of the steel wire is .1.0mm2 and that of the aluminium wire is 3.0 mm 2. What could be the minimum frequency of a tuning fork which can produce standing waves in the system with the joint as a node ? The density of aluminium is 2.6gcm−3and that of steel is 7.8gcm−3

View Solution
Knowledge Check
An aluminium wire and a steel wire of same cross-sectional of 10−2cm2 were connected together. A 10 kg block loaded on the compound wire as shown in figure. Waves are set up in the compound wire. The minimum frequency of excitation for which standing waves are observed with point A as a node is [L1=60cm,L2=86.6cm] density of aluminium =2.6g/cm3 and of steel=7.8g/cm3]
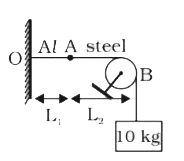 A223HzB423HzC327 HzD427 Hz
A223HzB423HzC327 HzD427 HzAn alumminium rod and steel wire of same length and cross-section are attached end to end. Then compound wire is hung fron a rigid support and load is suspended from the free end. Y for steel is (207) times of aluminium. The ratio of increase in length of steel wire to the aluminium wire is
A20:3B10:7C7:20D1:7
An aluminium wire of cross-sectionbal area 1×10−6m2 is joined to a steel wire of same cross-sectional ara. This compound wire is stretched on a sonometer, pulled by a weight of 10kg. The total length of the compound wire between the bridges is 1.5m, of which the aluminium is 0.6m and the rest is steel wire. Transverse vibrationas are set up in the wire by using an ecternal force of variable frequency. Find the lowest frequency of excitation for which standing waves are formed such that the joint in the wire is a node. What is the total number of nodes observed at this frequency, excluding the two at the ends of the wire? The density of aluminium is 2.6×103kg/m3 and that of steel is 1.04×104kg/m3.
View SolutionAn aluminium wire of cross-sectionbal area 1×10−6m2 is joined to a steel wire of same cross-sectional ara. This compound wire is stretched on a sonometer, pulled by a weight of 10kg. The total length of the compound wire between the bridges is 1.5m, of which the aluminium is 0.6m and the rest is steel wire. Transverse vibrationas are set up in the wire by using an ecternal force of variable frequency. Find the lowest frequency of excitation for which standing waves are formed such that the joint in the wire is a node. What is the total number of nodes observed at this frequency, excluding the two at the ends of the wire? The density of aluminium is 2.6×103kg/m3 and that of steel is 1.04×104kg/m3.
View SolutionAn aluminimum wire of cross - sectional area 1×10−6m2 is joined to a steel wire of the same cross - sectional area . This compound wire is stretched on a sonometer , pulled by a weight of 10kg. The total length of the compound wire between the bridges is 1.5m of which the aluminium wire is 0.6m and the rest is steel wire . Transverse vibrations are set up in the wire by using an external source of variable frequency . Find the lowest frequency of excitation for which standing waves are formed , such that the joint in the wire is a node . What is the total number of nodes observed at this frequency , excluding the two at the ends of the wire ? The density of aluminium is 2.6×103kg/m3 and that of steel is 1.04×104kg/m3
View SolutionA steel wire of length 50√3cm is connected to an aluminium wire of length 60cm and stretched between two fixed supports. The tension produced is 104N, if the cross section area of each wire is 1mm2. If a transverse wave is set up in the wire, find the lowest frequency for which standing waves with node at the joint are produced . (density of aluminimum =2.6gm/cm3 and density of steel =7.8gm/cm3).
View SolutionA sonometer wire of length 1 m is stretched by a weight of 10 kg. The fundamental frequency of vibration is 100 Hz. Determine the linear density of material of wire.
View SolutionAn aluminium wire of cross-sectional area (10−6)m2 is joined to a steel wire of the same cross-sectional area. This compound wire is stretched on a sonometer pulled by a weight of 10kg. The total length of the compound wire between the bridges is 1.5m of which the aluminium wire is 0.6m and the rest is steel wire. Transverse vibrations are setup in the wire by using an external source of variable frequency. Find the lowest frequency of excitation for which the standing waves are formed such that the joint in the wire is a node. What is the total number of nodes at this frequency? The density of aluminium is 2.6×(103)kg/m3 and that of steel is 1.04×104kg/m2(g=10m/s2)
View Solution
