In the figure PQ is a diameter of a circle with centre O. QR is a tangent to the circle equal to OQ. OT is perpendicular to PR. QT is produced to cut the circle at S Prove that SP=ST
Step by step video & image solution for In the figure PQ is a diameter of a circle with centre O. QR is a tangent to the circle equal to OQ. OT is perpendicular to PR. QT is produced to cut the circle at S Prove that SP = ST by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
In the adjoining figure 'O' is the centre of the circle and PQ, PR and ST are the three tangents. angleQPR = 50^(@) , then the value of angleSOT is :
View SolutionIn the given figure ,PR and ST are perpendiculars to tan- gent QR, PQ passes through centre O of the circle whose diameter is 10 cm . If PR = 9 cm what is the length (in cm.) of ST ?
View SolutionIf PQ and PR be the two tangents to a circle with centre O such that ∠QPR=120∘ then ∠POQ is
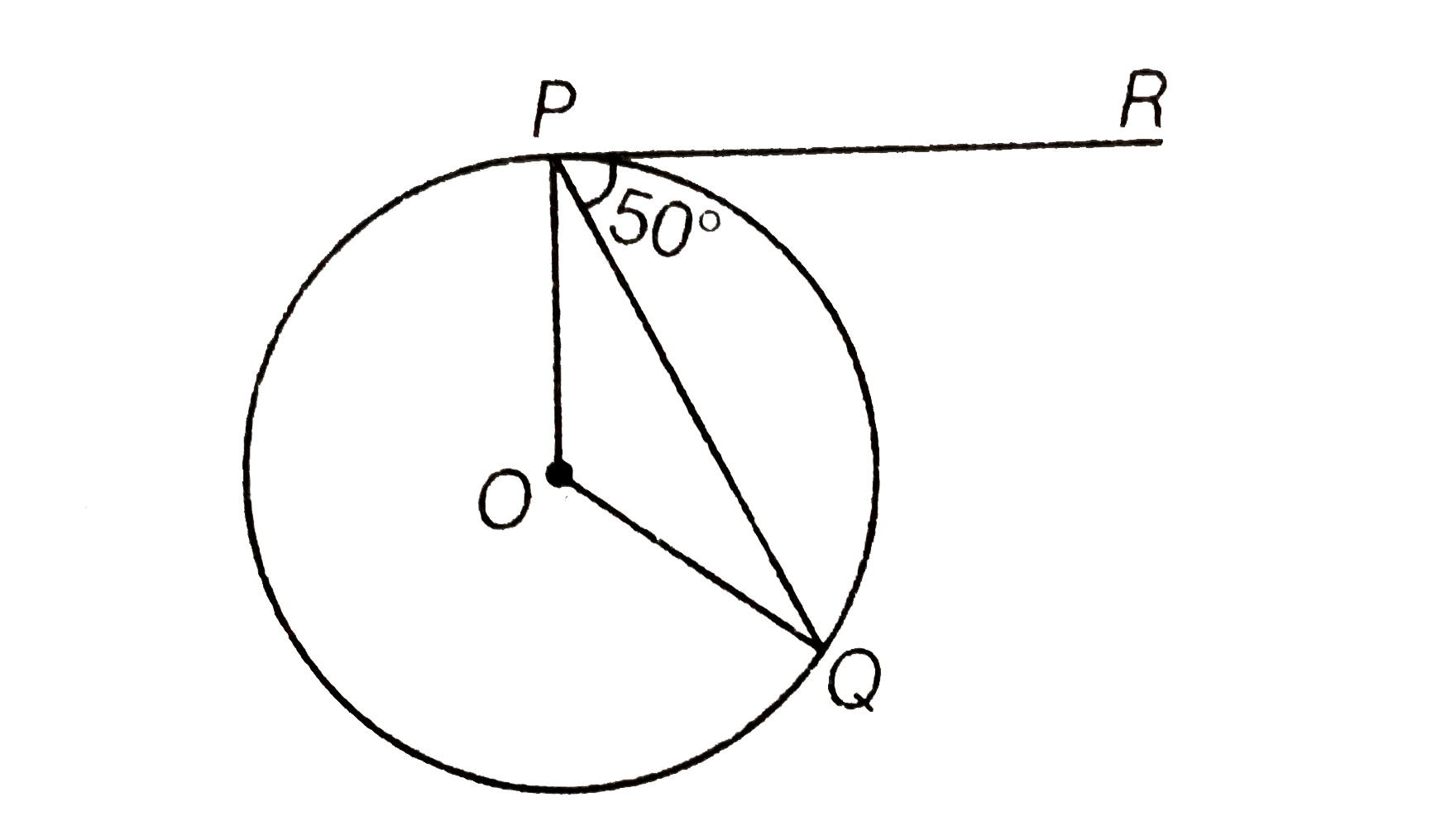
View SolutionIn figure, if O is the centre of a circle, PQ is a chord and the tangent PR at P makes an angle of 50∘ with PQ, then ∠POQ is equal to
View SolutionIn figure, PQ and PR are two tangents to a circle with centre O.
IF ∠QPR=46∘ , then ∠QOR equals
(a) 67∘

View SolutionPQ is tangent at a point R of the circle with centre O. If ST is a diameter of the circle and ∠TRQ=30∘ find ∠PRS
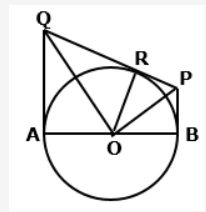
View SolutionIn the given figure, AB is diameter of the circle with centre O. AQ, BP and PRQ are tangents. Prove that OP and OQ are perpendicular to each other.
View SolutionPQ is tangent drawn from point P to a circle with centre O and QR is a diameter of the circle, such that ∠POR=120∘. Then, ∠OPQ=……...
View Solution
