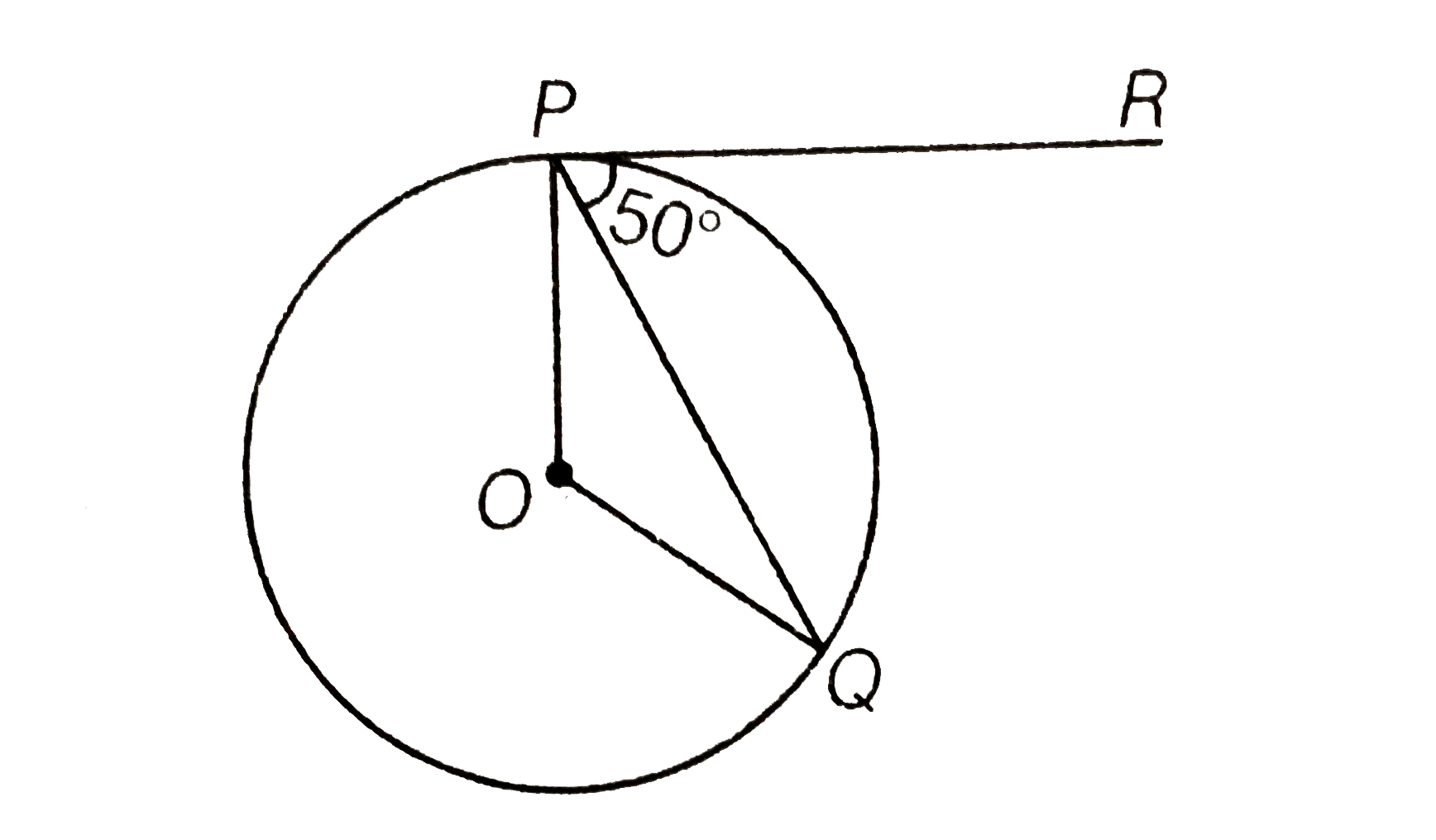
In figure, if O is the centre of a circle, PQ is a chord and the tangent PR at P makes an angle of 50∘ with PQ, then ∠POQ is equal to
100∘
80∘
90∘
75∘
The correct Answer is:A
Given, ∠QPR=50∘
We know that, the tangent at any point of a circle is perpendicular to the through the point of contact.
∴∠OPR=90∘
⇒∠OPQ+∠QPR=90∘ [from figure]
⇒∠OPQ=90∘−50∘=40∘
[∵∠QPR=50∘]
Now, OP = OQ = Radius of circle
∴∠OQP=∠OPQ=40∘
[since, angle opposite to equal sides are equal]
In ΔOPQ, ∠O+∠P+∠Q=180∘
[since, sum of angles of a triangle =180∘]
⇒∠O=180∘−(40∘+40∘) [∵∠P=40∘=∠Q]
=180∘−80∘=100∘
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - EXERCISE 9.2 VERY SHORT ANSWER TYPE QUESTIONS10videos
CIRCLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - EXERCISE 9.3 SHORT ANSWER TYPE QUESTIONS10videos
CIRCLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - Long Answer Type Questions10videos
ARITHMETIC PROGRESSIONS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Exercise 10.4 Long Answer type Questions7videos
CONSTRUCTIONS
Similar Questions
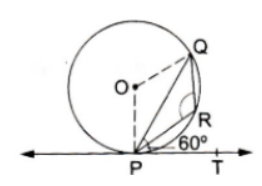
In the adjoining figure, PQ is a chord of a circle and PT is the tangent at P such that ∠QPT=60∘.Find ∠PRQ.
 View Solution
View SolutionIn figure PQ is tangent to the circle with centre at O at the point B , if ∠AOB=100∘, then ∠ABP is equal to
 View Solution
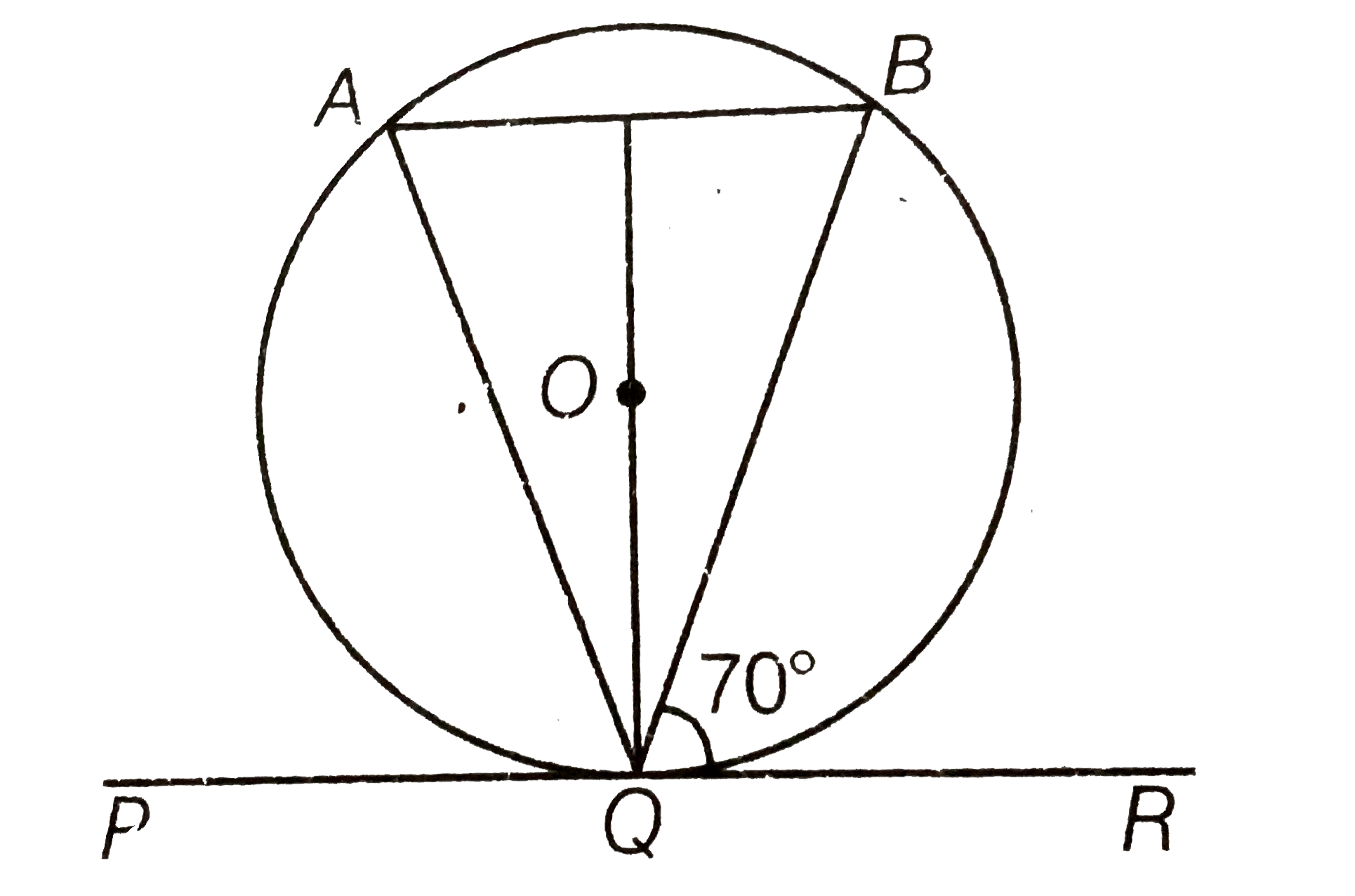
View SolutionIn figure, if PQR is the tangent to a circle at Q whose centre is O, AB is a chord parallel to PR and ∠BQR=70∘ then ∠AQB is equal to
 View Solution
View SolutionIn figure, if PA and PB are tangents to the circle with centre O such that ∠APB=50∘, then ∠OAB is equal to
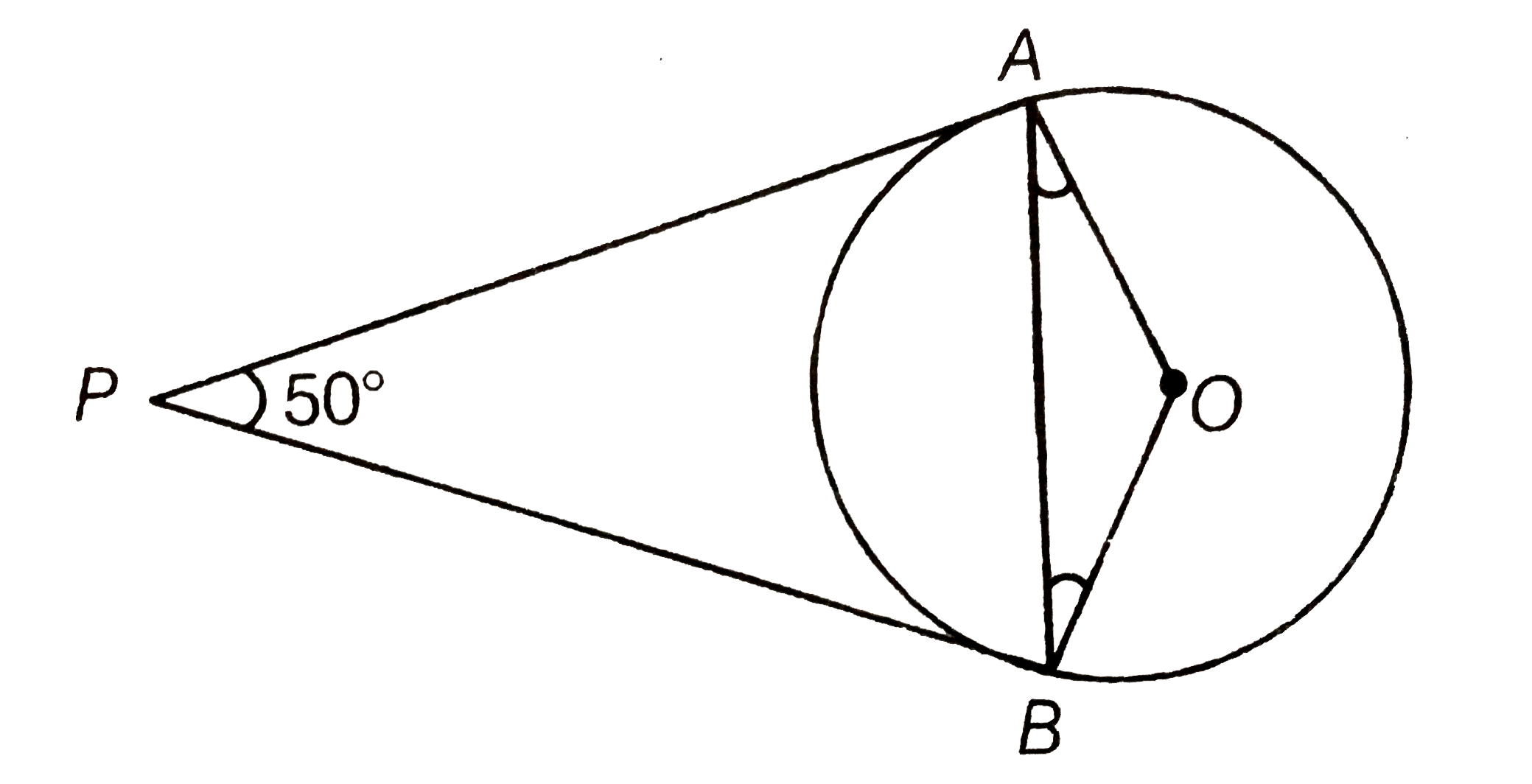 View Solution
View SolutionIn figure-3, PQ is tangent to the circle with centre at O, at the point B. if ∠AOB=100∘, then ∠ABP is equal to
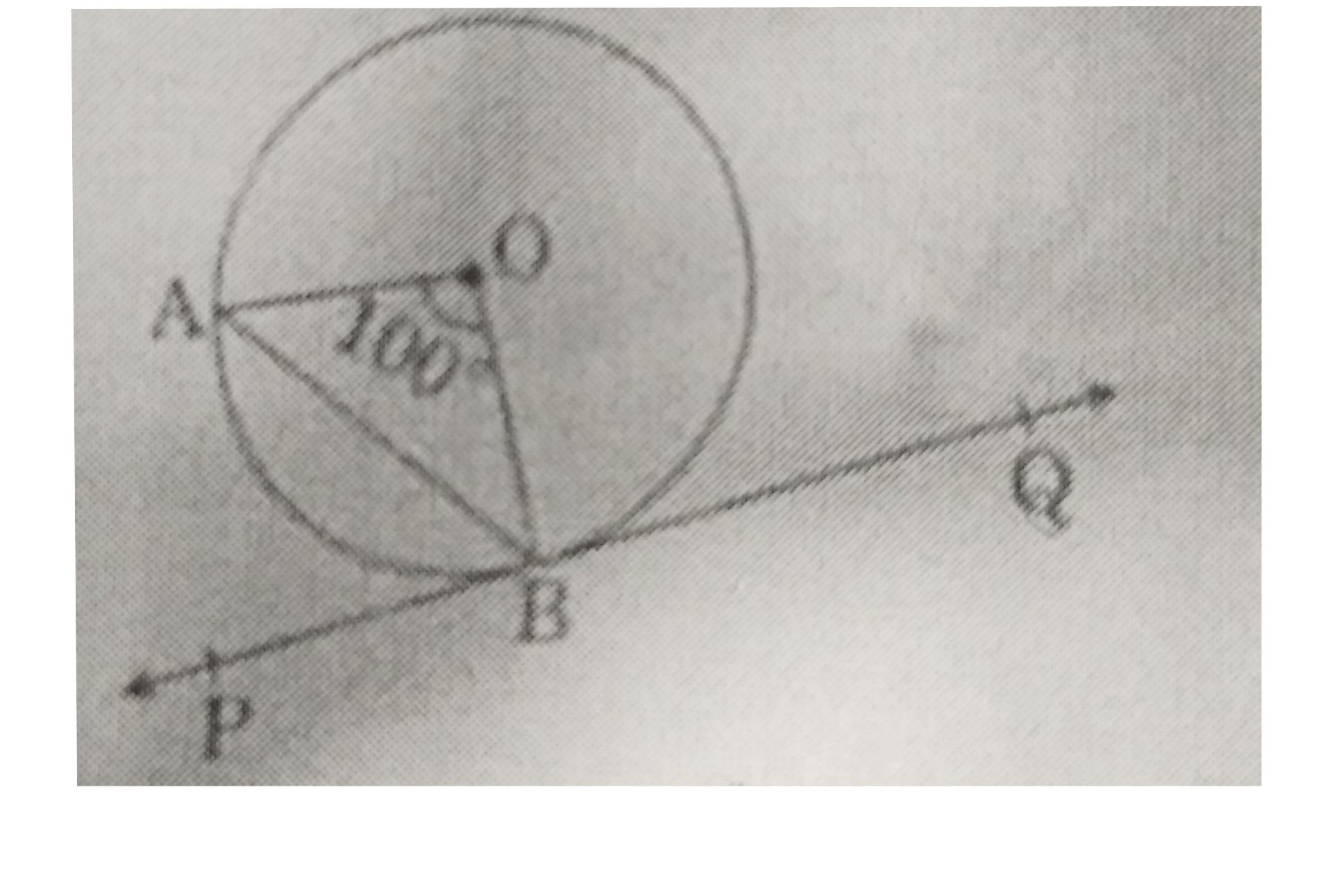 View Solution
View SolutionIn the following figure, if PQ=R (P is the centre of the bigger circle) and the shaded area is equal to A, then the radius of the inner circle is equal to -
 View Solution
View SolutionIn the given figure, if TP and TQ are tangents to a circle with centre O, so that ∠POQ=110∘, then ∠PTQ is
View SolutionIn Figure-2 PQ is tangent to the circle with centre at O , at the point B. If ∠AOB = 100∘ , then ∠ABP is equal to
(A) 50∘
(B) 40∘
(C) 60∘
(D) 80∘View SolutionFrom a point P which is at a distance of 13 cm from the center O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle is drawn. Then, the area of the quadrilateral PQOR is
View SolutionIn figure, AB is a chord of the circle and AOC is its diameter such that ∠ACB=50∘. If AT is the tangent to the circle at the point A, then ∠BAT is equal to
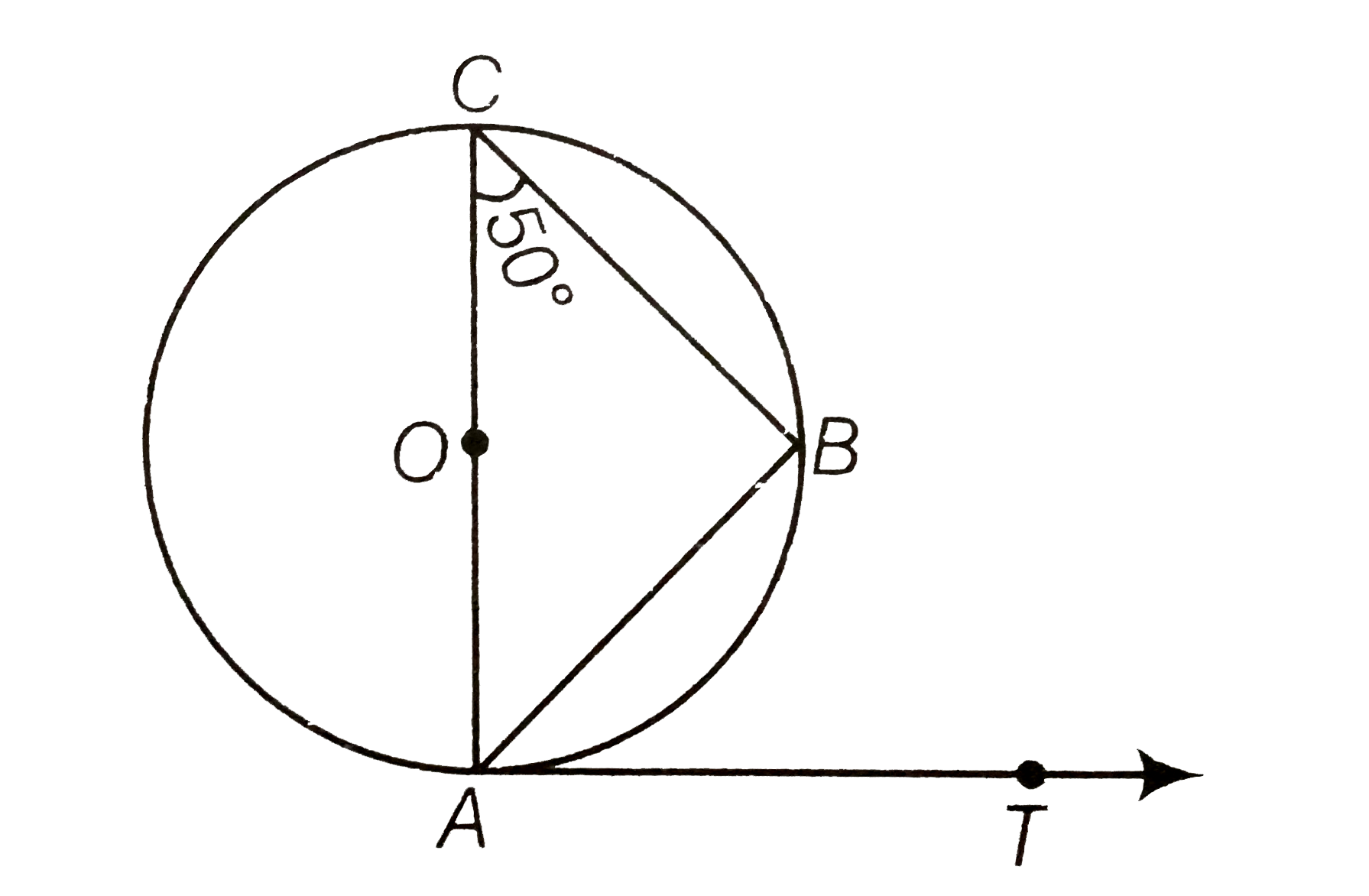 View Solution
View Solution

