A particle of mass 0.6kg is subjected to a force of F= -kx with k= 15 Nm−1. What will be its initial acceleration if it is released from a point 20 cm away from the origin ?
The correct Answer is:As F=ma so F =-kx =ma
a=−kxm
for x=20cm. ⇒a=−5m/s2
To find the initial acceleration of a particle subjected to a force of F=−kx, we can follow these steps:
Step 1: Identify the given values
- Mass of the particle, m=0.6kg
- Spring constant, k=15Nm−1
- Initial position from the origin, x=20cm=0.2m (conversion from centimeters to meters)
Step 2: Write the expression for the force
The force acting on the particle is given by:
F=−kx
Substituting the values of k and x:
F=−15×0.2
Calculating this gives:
F=−3N
Step 3: Use Newton's second law to find acceleration
According to Newton's second law, the force is also given by:
F=ma
Where a is the acceleration. We can set the two expressions for force equal to each other:
−ma=−kx
Substituting the values we have:
−0.6a=−3
Step 4: Solve for acceleration
Now, we can solve for a:
0.6a=3
a=30.6
Calculating this gives:
a=5m/s2
Step 5: Determine the direction of acceleration
Since the force was negative, indicating that it acts in the opposite direction to the displacement, the acceleration will also be in the opposite direction. Therefore, we can express the acceleration as:
a=−5m/s2
Final Answer
The initial acceleration of the particle is:
−5m/s2
- Mass of the particle, m=0.6kg
- Spring constant, k=15Nm−1
- Initial position from the origin, x=20cm=0.2m (conversion from centimeters to meters)
The force acting on the particle is given by:
F=−kx
Substituting the values of k and x:
F=−15×0.2
Calculating this gives:
F=−3N
According to Newton's second law, the force is also given by:
F=ma
Where a is the acceleration. We can set the two expressions for force equal to each other:
−ma=−kx
Substituting the values we have:
−0.6a=−3
Now, we can solve for a:
0.6a=3
a=30.6
Calculating this gives:
a=5m/s2
Since the force was negative, indicating that it acts in the opposite direction to the displacement, the acceleration will also be in the opposite direction. Therefore, we can express the acceleration as:
a=−5m/s2
The initial acceleration of the particle is:
−5m/s2
Topper's Solved these Questions
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - 3 Marks Questions & Numericals21videos
NEWTON'S LAWS OF MOTION
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - 5 Marks Questions2videos
NEWTON'S LAWS OF MOTION
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Laws Of Motion20videos
NEWTON'S LAWS OF MOTION
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - MECHANICAL WAVESEXERCISE - MCQ20videos
MECHANICAL WAVES
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - PROPERTIES OF MATTEREXERCISE - MULTIPLE CHOICE QUESTIONS (MCQs)20videos
PROPERTIES OF MATTER
Similar Questions
A particle of mass 0.6kg is subjected to a force of F= -kx with k= 15 Nm−1. What will be its initial acceleration if it is released from a point 20 cm away from the origin ?
View SolutionA particle of mass 0.3 kg is subjected to a force F = - kx , Where = 15Nm−1 . What will be its initial acceleration when particle is released from a point 20 cm away from origin ?
View Solution
Knowledge Check
- Question 1 - Select One
A particle of mass 0.3 kg is subjected to a force F=−kx with k=15N/m. What will be its initial acceleration if it is released from a point 20 cm away from th origin?
A5m/s2B10m/2C3m/s2D15m/s2 - Question 2 - Select One
A particle of mass 0.3 kg subject to a force F=−kx with k=15N/m. What will be its initial acceleration if it is released from a point 20cm away from the origin?
A(a) 15m/s2B(b) 3m/s2C(c) 10m/s2D(d) 5m/s2 - Question 3 - Select One
A particle of mass 0.3kg is subjected to a force F=kx with k=15N/m and x being its distance from the origin. What will be its initial acceleration if it is released from a point 20cm away from the origin.
A5ms−2B10ms−2C3ms−2D15ms−2
A particle of mass 1 kg is subjected to a force which varies with distance as shown. If it starts it s journey from rest at x=0. then its velocity at x=15 m is
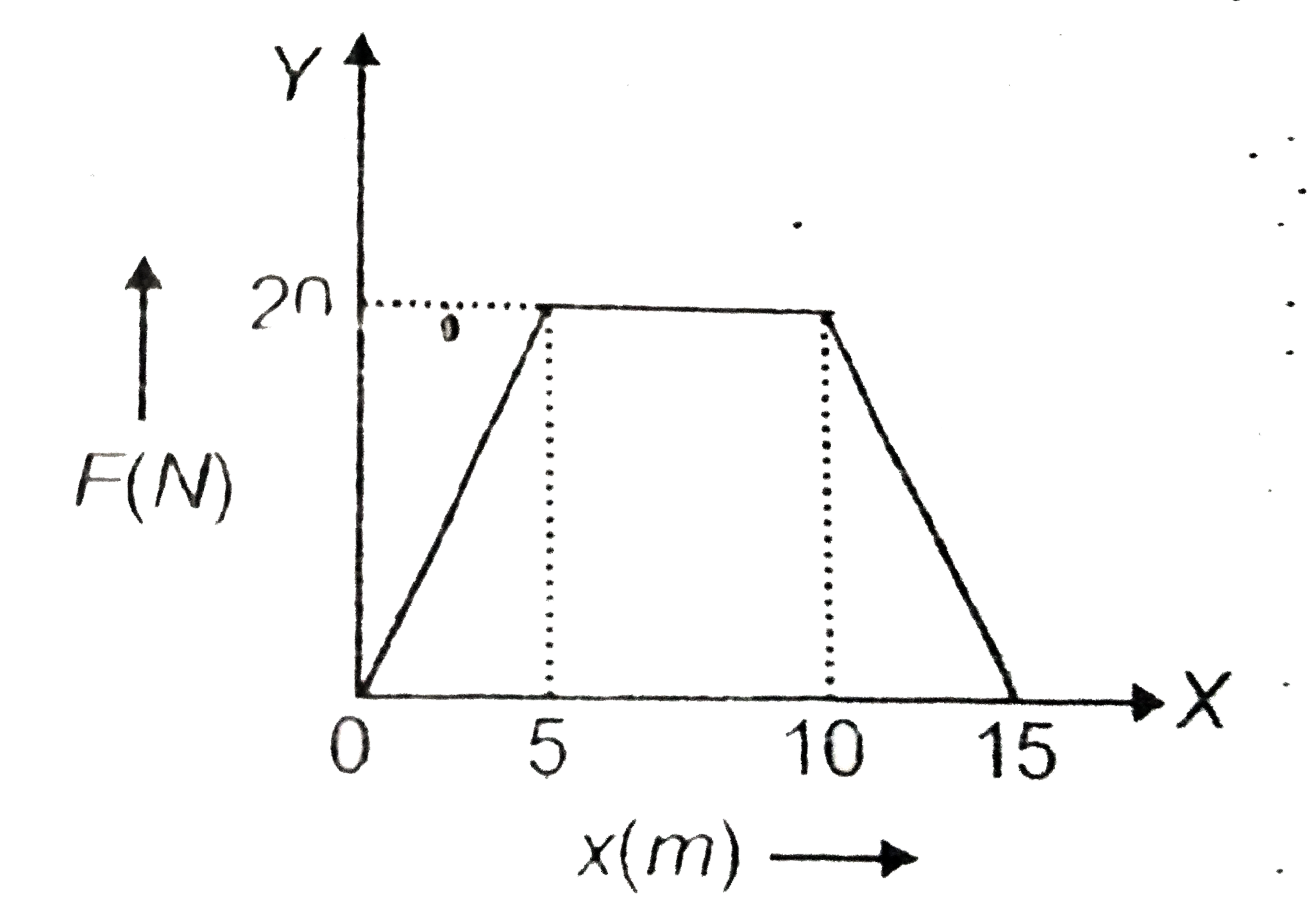 View Solution
View Solution
A particle of mass 0.1 kg is subjected to a force which varies with distance as shown in figure. If it starts its journey from rest at x=0, its velocity at x=12m isView SolutionA particle of mass m is acted upon by a force F=t2−kx . Initially , the particle is at rest at the origin. Then
View SolutionA particle of mass 0.1 kg is subjected to a force which varies with distance as shown in figure.
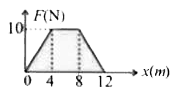
If it starts its journey from rest at x = 0, its velocity at x=12 m isView SolutionA particle of mass 0.1 kg is subjected to a force which varies with distance as shown in figure. If it starts its journey from rest at x = 0, its velocity at x = 12 m is
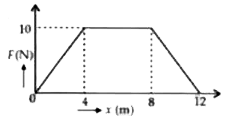 View Solution
View Solution

