A voltage, $E = E_{0} sin ω t$ is applied across an inductor L. Obtain an expression for the current.

Video Solution

Answer

Step by step video & image solution for A voltage, E = E_(0) sin omega t is applied across an inductor L. Obtain an expression for the current. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS MOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

UNIT–III & UNIT–IV MAGNETIC EFFECTS OF CURRENT AND MAGNETISM & E.M.I. AND ALTERNATING CURRENTBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - UNIT–III & UNIT–IV MAGNETIC EFFECTS OF CURRENT AND MAGNETISM & E.M.I. AND ALTERNATING CURRENTEXERCISE - LONG ANSWER QUESTIONS (5 Marks)
5 Videos
UNIT–III & UNIT–IV MAGNETIC EFFECTS OF CURRENT AND MAGNETISM & E.M.I. AND ALTERNATING CURRENTBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - UNIT–III & UNIT–IV MAGNETIC EFFECTS OF CURRENT AND MAGNETISM & E.M.I. AND ALTERNATING CURRENTEXERCISE - (NUMERICALS)
57 Videos
UNIT–III & UNIT–IV MAGNETIC EFFECTS OF CURRENT AND MAGNETISM & E.M.I. AND ALTERNATING CURRENTBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - UNIT–III & UNIT–IV MAGNETIC EFFECTS OF CURRENT AND MAGNETISM & E.M.I. AND ALTERNATING CURRENTEXERCISE - SHORT ANSWER QUESTIONS (2 Marks)
41 Videos
SAMPLE QUESTION PAPER 2019BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SAMPLE QUESTION PAPER 2019EXERCISE - Section C
19 Videos

Knowledge Check

An alternating voltage $E = E_{0} sin ω t$ , is applied across a coil of inductor L. The current flowing through the circuit at any instant is
A $\frac{E_{0}}{ω L} sin (ω t + π / 2)$
B $\frac{E_{0}}{ω L} sin (ω t - π / 2)$
C $E_{0} ω L sin (ω t - π / 2)$
D $E_{0} ω L sin (ω t + π / 2)$
An alternating voltage $V = 100 sin ω t$ is applied across an $L C R$ circuit as shown. At the instant when voltage drop across source is $50 \sqrt{3}$ volts then at that instant
$R = 30 Ω X_{L} = 60 Ω X_{C} = 20 Ω$

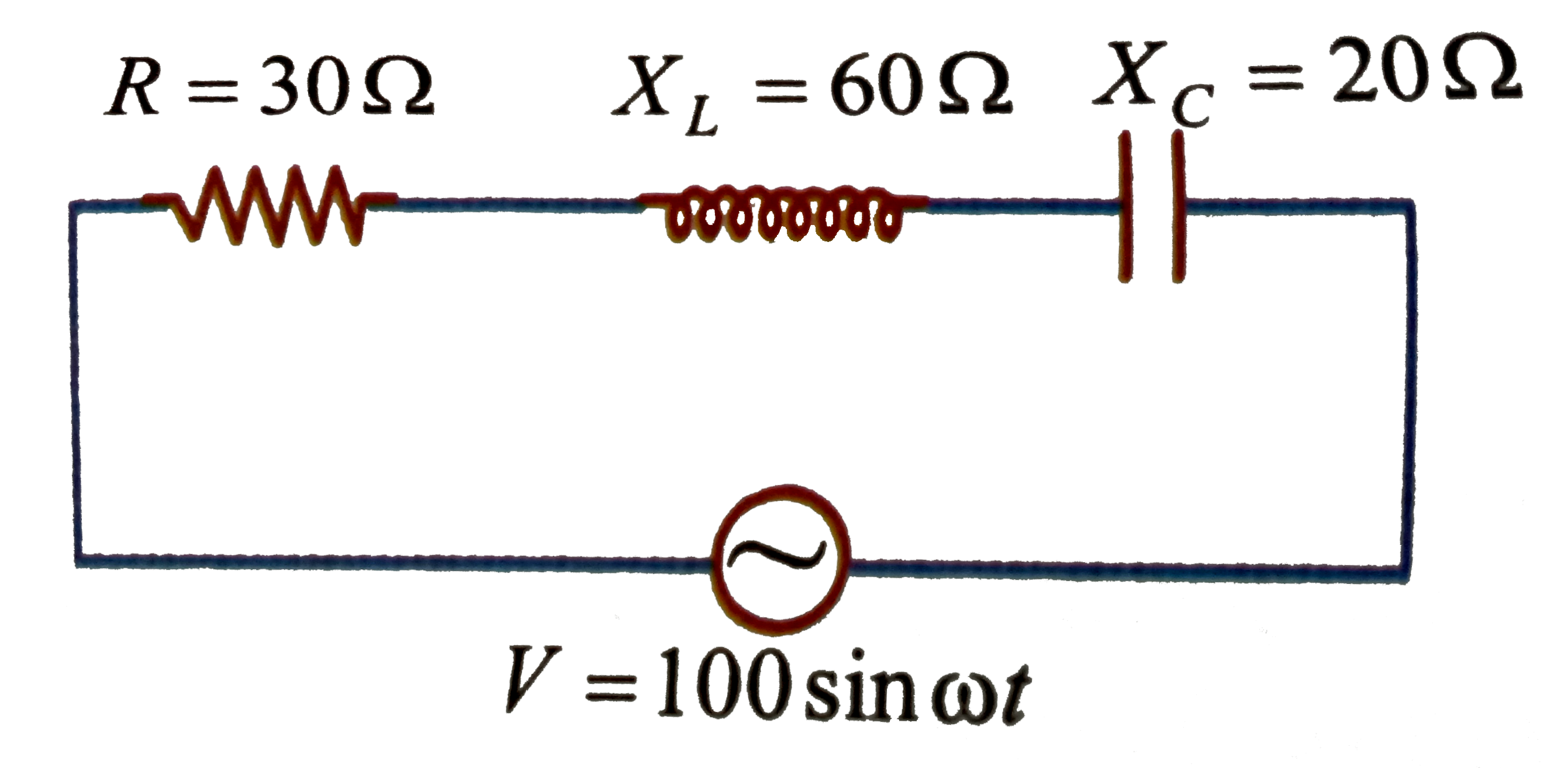Avoltage drop across inductor is $(120 {cos 7}^{\circ})$ volts
Bvoltage drop across capacitor is $(40 {cos 173}^{\circ})$ volts
Cvoltage drop across resistor is $(60 {cos 7}^{\circ})$ volts
DAll the above
The alternating emf of $e = e_{0}$ sin $ω t$ is applied across capacitor C. the current through the circuit is given by
A $I = I_{0} sin ω t$
B $I = I_{0} sin (ω t + \frac{π}{2})$
C $I = I_{0} sin (ω t - \frac{π}{2})$
D $I = I_{0} sin (ω t - π)$

CBSE COMPLEMENTARY MATERIAL-UNIT–III & UNIT–IV MAGNETIC EFFECTS OF CURRENT AND MAGNETISM & E.M.I. AND ALTERNATING CURRENT-SHORT ANSWERS QUESTIONS (3 Marks)

Home
Ask Doubt
Profile

A voltage, E=E0sinωt is applied across an inductor L. Obtain an expression for the current.

Topper's Solved these Questions

Similar Questions

Knowledge Check

An alternating voltage E=E0sinωt , is applied across a coil of inductor L. The current flowing through the circuit at any instant is

An alternating voltage V=100sinωt is applied across an LCR circuit as shown. At the instant when voltage drop across source is 50√3 volts then at that instant R=30Ω XL=60Ω XC=20Ω

The alternating emf of e=e0 sin ωt is applied across capacitor C. the current through the circuit is given by

CBSE COMPLEMENTARY MATERIAL-UNIT–III & UNIT–IV MAGNETIC EFFECTS OF CURRENT AND MAGNETISM & E.M.I. AND ALTERNATING CURRENT-SHORT ANSWERS QUESTIONS (3 Marks)

A voltage, $E = E_{0} sin ω t$ is applied across an inductor L. Obtain an expression for the current.

An alternating voltage $E = E_{0} sin ω t$ , is applied across a coil of inductor L. The current flowing through the circuit at any instant is

An alternating voltage $V = 100 sin ω t$ is applied across an $L C R$ circuit as shown. At the instant when voltage drop across source is $50 \sqrt{3}$ volts then at that instant
$R = 30 Ω X_{L} = 60 Ω X_{C} = 20 Ω$

The alternating emf of $e = e_{0}$ sin $ω t$ is applied across capacitor C. the current through the circuit is given by