The time period of a physical pendulum about some pivot point is T. When we take another pivot point, opposite of the first one such that the centre of mass of the physical pendulum lies on the line joining these two pivot points, we obtain the same time period. If the two points are separated by a distance L, then the time period T is
2π√Lg
π√Lg
2π√L2g
π√2Lg
The correct Answer is:A
To solve the problem, we need to derive the expression for the time period T of a physical pendulum when pivoting about two different points that are separated by a distance L.
1. Understanding the Physical Pendulum:
A physical pendulum oscillates about a pivot point, and its time period T can be expressed using the formula:
T=2π√Imgh
where I is the moment of inertia about the pivot point, m is the mass of the pendulum, g is the acceleration due to gravity, and h is the distance from the pivot to the center of mass.
2. Identifying the Two Pivot Points:
Let’s denote the two pivot points as P1 and P2. The distance between these two points is L. The center of mass C of the pendulum lies on the line joining these two pivot points.
3. Moment of Inertia Calculation:
The moment of inertia I about the first pivot point P1 can be expressed as:
IP1=IC+md21
where IC is the moment of inertia about the center of mass, m is the mass of the pendulum, and d1 is the distance from the center of mass to the pivot point P1.
Similarly, for the second pivot point P2:
IP2=IC+md22
where d2=L−d1 (since the total distance between the two pivot points is L).
4. Time Period for Both Pivot Points:
The time period for the first pivot point P1 is:
T1=2π√IP1mgd1=2π√IC+md21mgd1
The time period for the second pivot point P2 is:
T2=2π√IP2mgd2=2π√IC+m(L−d1)2mg(L−d1)
5. Equating the Time Periods:
According to the problem, the time periods T1 and T2 are equal:
T1=T2
6. Simplifying the Expression:
Since both expressions are equal, we can set them equal to each other and simplify:
√IC+md21gd1=√IC+m(L−d1)2g(L−d1)
7. Finding the Time Period:
After simplifying the above equation, we can derive the expression for the time period T in terms of the distance L:
T=2π√Lg
Final Answer:
The time period T of the physical pendulum is:
T=2π√Lg
A physical pendulum oscillates about a pivot point, and its time period T can be expressed using the formula:
T=2π√Imgh
where I is the moment of inertia about the pivot point, m is the mass of the pendulum, g is the acceleration due to gravity, and h is the distance from the pivot to the center of mass.
Let’s denote the two pivot points as P1 and P2. The distance between these two points is L. The center of mass C of the pendulum lies on the line joining these two pivot points.
The moment of inertia I about the first pivot point P1 can be expressed as:
IP1=IC+md21
where IC is the moment of inertia about the center of mass, m is the mass of the pendulum, and d1 is the distance from the center of mass to the pivot point P1.
IP2=IC+md22
where d2=L−d1 (since the total distance between the two pivot points is L).
The time period for the first pivot point P1 is:
T1=2π√IP1mgd1=2π√IC+md21mgd1
The time period for the second pivot point P2 is:
T2=2π√IP2mgd2=2π√IC+m(L−d1)2mg(L−d1)
According to the problem, the time periods T1 and T2 are equal:
T1=T2
Since both expressions are equal, we can set them equal to each other and simplify:
√IC+md21gd1=√IC+m(L−d1)2g(L−d1)
After simplifying the above equation, we can derive the expression for the time period T in terms of the distance L:
T=2π√Lg
The time period T of the physical pendulum is:
T=2π√Lg
Topper's Solved these Questions
Similar Questions
A rigid body is to be suspended like a physical pendulum so as to have a time period of T=0.2π second for small amplitude oscillations. The minimum distance of the point of suspension from the centre of mass of the body is l1=0.4m to get this time period. Find the maximum distance (l2) of a point of suspension from the centre of mass of the body so as to get the same time period. [g=10m/s2]
View SolutionIn Fig 15.19a, a meter stick swings about a pivot point at one end, at distance h from the stick's center of mass.
What is the distance L0 between the pivot point O of the stick and the center of oscillation of the stick?View Solution
Knowledge Check
- Question 1 - Select One
The temperature of a physical pendulum, whose time period is T, is raised by Δθ. The change in its time period is
A12αΔθB2alpheTΔθC12αΔθD2 alpha Delata theta - Question 2 - Select One
If the time period of a pendulum is 1sec, then what is the length of the pendulum at point of intersection of l−T and l−T2 graph.
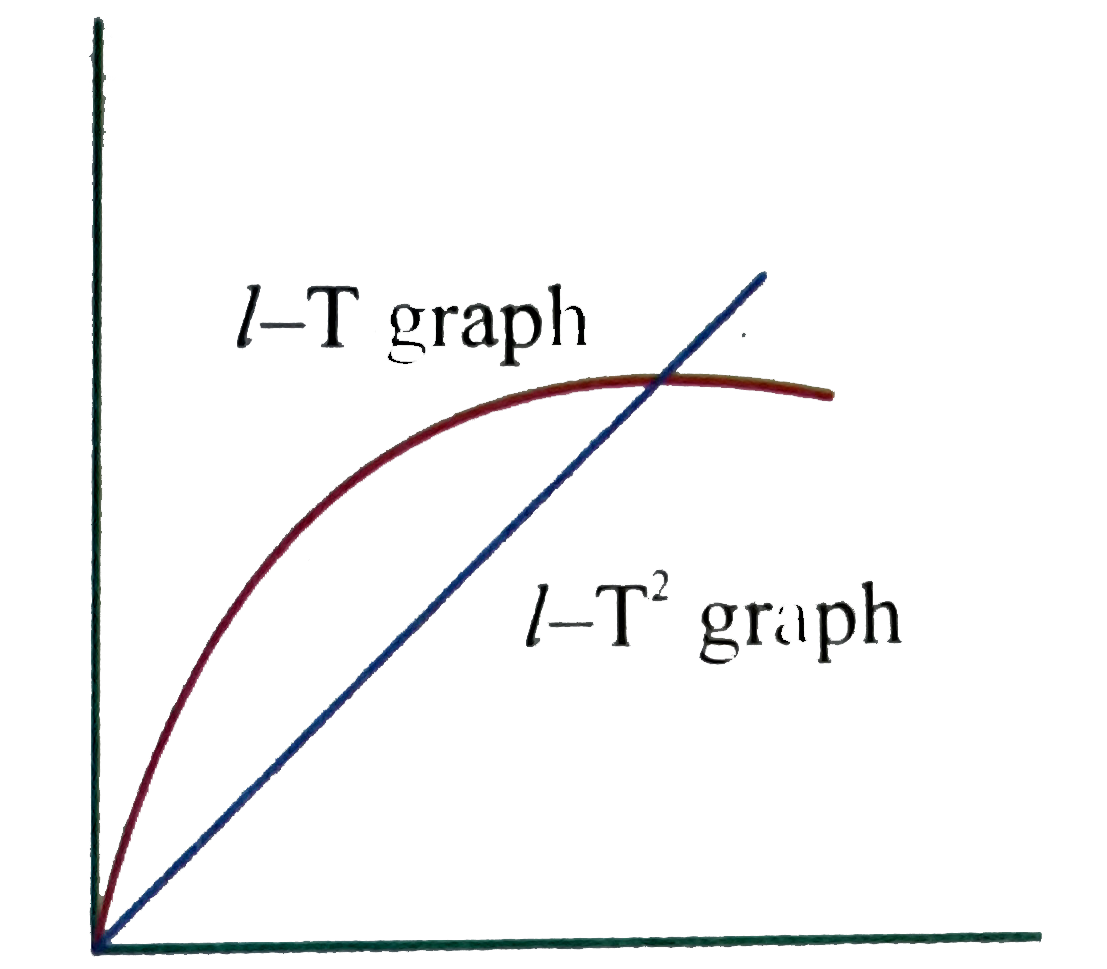 A25cmB21cmC22cmD27cm
A25cmB21cmC22cmD27cm - Question 3 - Select One
The two spring-mass system, shown in the figure, oscillates with a period T. If only one spring is used, the time period will be
 AT√2BT2C√2TD2T
AT√2BT2C√2TD2T
The two spring-mass system, shown in the figure, oscillates with a period T. If only one spring is used, the time period will be
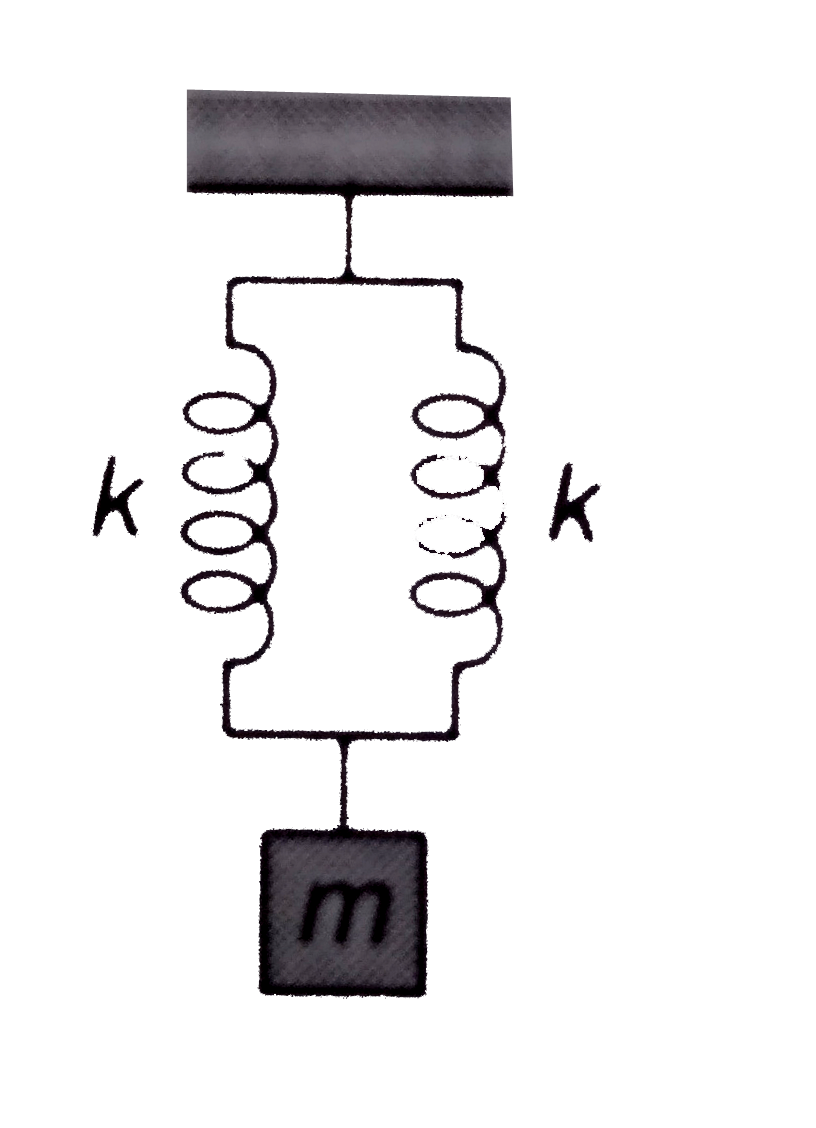 View Solution
View Solution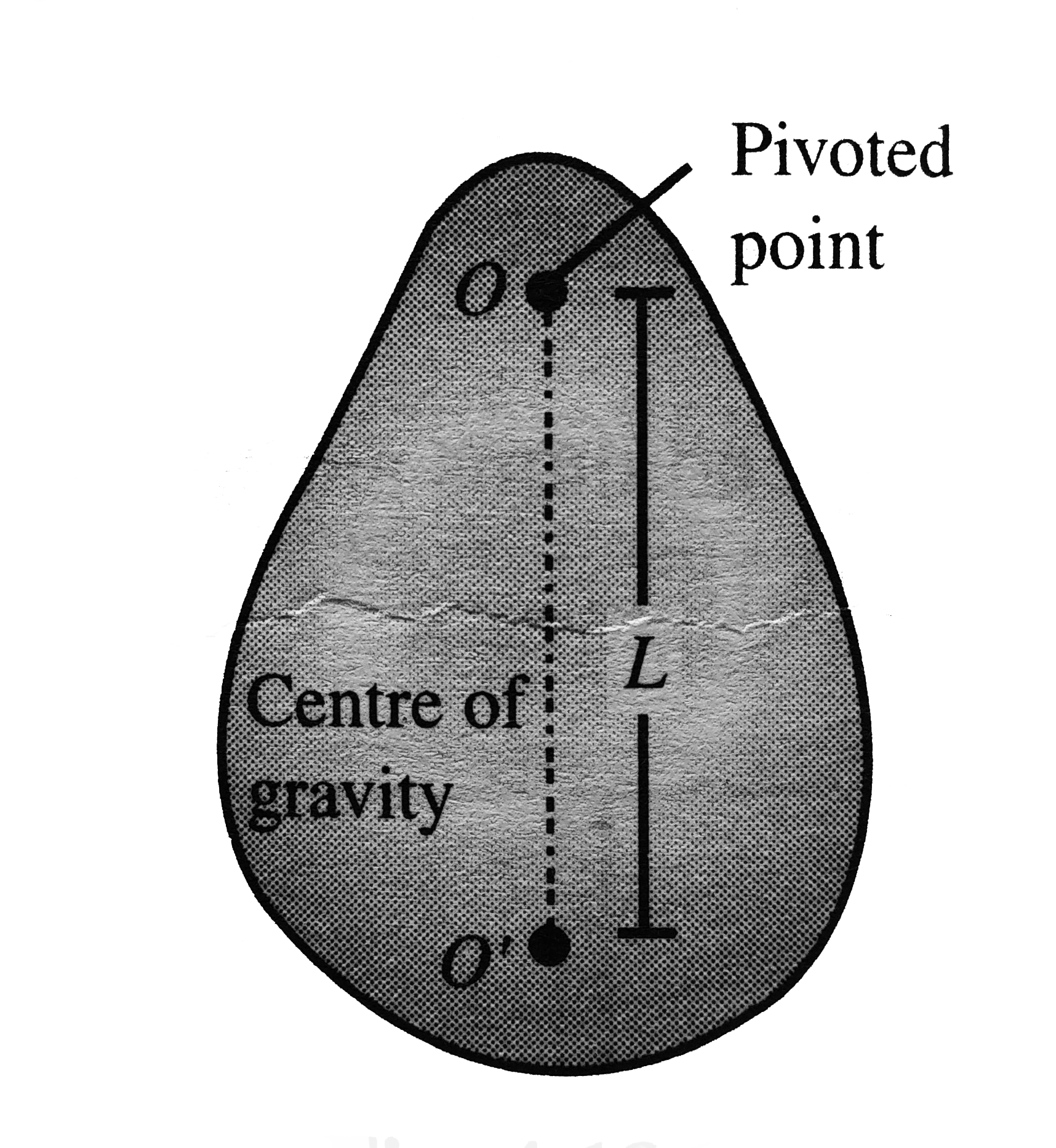
In physical pendulum, the time period for small oscillation is given by T=2π√IMgd where I is the moment of inertial of the body about an axis passing through a pivoted point O and perpendicular to the plane of oscillation and d is the separation point between centre of gravity and the pivoted point. In the physical pendulum a speacial point exists where if we concentrate the entire mass of body, the resulting simple pendulum (w.r.t. pivot point O) will have the same time period as that of physical pendulum This point is termed centre of oscillation.
T=2π√IMgd=2π√Lg Moreover, this point possesses two other important remarkable properties:
Property I: Time period of physical pendulum about the centre of oscillation (if it would be pivoted) is same as in the original case.
Property II: If an impulse is applied at the centre of oscillatioin in the plane of oscillation, the effect of this impulse at pivoted point is zero. Because of this property, this point is also known as the centre of percussion. From the given information answer the following question:
Q. A uniform rod of mass M and length L is pivoted about point O as shown in Figgt It is slightly rotated from its mean position so that it performs angular simple harmonic motion. For this physical pendulum, determine the time period oscillation.View SolutionIn physical pendulum, the time period for small oscillation is given by T=2π√IMgd where I is the moment of inertial of the body about an axis passing through a pivoted point O and perpendicular to the plane of oscillation and d is the separation point between centre of gravity and the pivoted point. In the physical pendulum a speacial point exists where if we concentrate the entire mass of body, the resulting simple pendulum (w.r.t. pivot point O) will have the same time period as that of physical pendulum This point is termed centre of oscillation.
T=2π√IMgd=2π√Lg Moreover, this point possesses two other important remarkable properties:
Property I: Time period of physical pendulum about the centre of oscillation (if it would be pivoted) is same as in the original case.
Property II: If an impulse is applied at the centre of oscillatioin in the plane of oscillation, the effect of this impulse at pivoted point is zero. Because of this property, this point is also known as the centre of percussion. From the given information answer the following question:
Q. If an impulse J is applied at the centre of oscillation in the plane of oscillation, then angular velocity of the rod will be .
 View Solution
View SolutionFor a bar pendulum the distance between two points of minimum time period is
View SolutionTwo pendulums have time periods T and 5T/4. They start SHM at the same time from the mean position After how many oscillations of the smaller pendulum they will be again in the same phase:
View Solution

