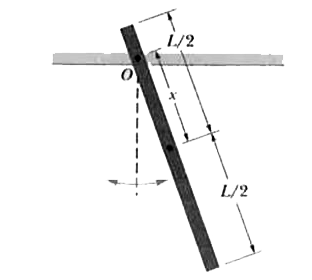
In Fig 15.19a, a meter stick swings about a pivot point at one end, at distance h from the stick's center of mass.
What is the distance L0 between the pivot point O of the stick and the center of oscillation of the stick?
Calculations: We want the length L0 of the simple pendulum (drawn in Fig 15.19b) that has the same period as the physical pendulum (the stick) of Fig 15.19a. Setting Eqs. 15.44 and 15.47 equal yields.
T=2π√L0g=2π√2L3g
You can see by inspection that
Lv=23L
=(23)(100cm)=66.7cm
In Fig 15.19a point P marks this distance from suspension point O. Thus, point P is the stick.s center of oscillation for the given suspension point. Point P would be different for a different suspension choice.

(a) A meter stick suspended from one end as a physical pendulum. (b) A simple pendulum whose length L0 is chosen so that the periods of the two pendulums are equal. Point P on the pendulum of (a) marks the center of oscillation.
Topper's Solved these Questions
- OSCILLATIONSBOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Checkpoint
8 Videos
- OSCILLATIONSBOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Problems
39 Videos
- MOTION IN TWO AND THREE DIMENSIONSBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MATRIX-MATCH)
10 Videos
- PHOTONS AND MATTER WAVESBOOK - RESNICK AND HALLIDAYCHAPTER - PHOTONS AND MATTER WAVESEXERCISE - PRACTICE QUESTIONS(Integer Type)
4 Videos
Similar Questions
In Fig 15.19a, a meter stick swings about a pivot point at one end, at distance h from the stick's center of mass.
What is the period of oscillation T?
View SolutionA uniform circular disc of mass M and radius R is pivoted at distance x above the centre of mass of the disc, such that the time period of the disc in the vertical plane is infinite. What is the distance between the pivoted point and centre of mass of the disc ?
View Solution
Knowledge Check
A strick is thrown in the air and lands on the ground at some distance from the centre of mass of the stick will move along a paranolic path
Ain all casesBonly if the stick is uniformConly if the stick has linear motion but no rotational motionDonly if the stick has a shape such that its centre of mass is located at some point on it and not outside itA stick is thrown in the air and lands at some distance from the thrower . The centre of mass of the stick will move along a parabolic path
AIn all casesBonly iif the stick is uniformConly if the stick does not have any rotational motionDOnly If the centre of mass of the stick lies at some point on it and not outside it
A uniform circular disc of mass M and radius R is pivoted at distance x above the centre of mass of the disc, such that the time period of the disc in the vertical plane is infinite. What is the distance between the pivoted point and centre of mass of the disc ?
View SolutionIn Fig. 15.33, a stick of length L= 1.65 m oscillates as a physical pendulum. (a) What value of distance x between the stick's center of mass and its pivot point O gives the least period? (b) What is that least period?
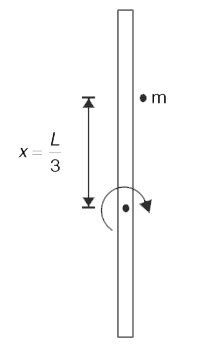
View SolutionA uniform thin stick of mass M=24kg and length L rotates on a friction less horizontal plane, with its centre of mass stationary. A particle of mass m is placed on the plane at a distance x=L3 from the centre of the stick . This stick hits the particle elastically
(a) Find the value of m so that after the collision, there is no rotational motion of the stick
(b) For what minimum of x can we get a value of ‘m’ so that the rod has no rotational motion after elastic collision ?
View SolutionA stick of length L=2.0m is leaned against a wall as shown. It is released from a position when θ=60∘. The end A of the stick remains in contact with the wall and its other end B remains in contact with the floor as the stick slides down. Find the distance travelled by the centre of the stick by the time it hits the floor.

View SolutionA metre stick is balanced on a knife edge at its centre. When two coins, each of mass 5 g are put one on top of the other at the 12.0 cm mark, the stick is found to be balanced at 45.0 cm, what is the mass of the meter stick ?
View SolutionA metre stick is balanced on a knife edge at its centre. When two coins, each of mass 6 g put one on top of the other at the 12.0 cm mark, the stick is found to be balanced at 45.0 cm. What is the mass of the metre stick?
View Solution
