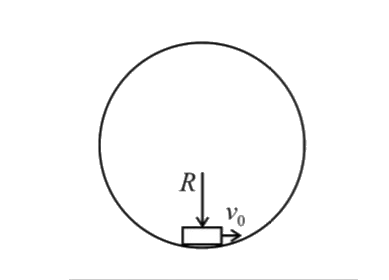
A hollow vertical cylinder of radius R and height h has a smooth internal surface. A small particle is held in contact with the inner side of upper rim at a point P. It is given a horizontal speed v0 tangential to rim. It leaves the lower rim at point Q, vertically below P. The number of revolutions made by the particle will be [Take acceleration due to gravity g]
h2πR
v0h√h2g
v02πR√2hg
v0πg√2gh2R
The correct Answer is:C
To solve the problem of determining the number of revolutions made by a particle inside a hollow vertical cylinder, we can follow these steps:
1. Understanding the Setup:
- We have a hollow vertical cylinder with radius R and height h.
- A particle is placed at the top rim (point P) and given a horizontal speed v0 tangential to the rim.
2. Motion of the Particle:
- As the particle moves, it will experience two types of motion: horizontal (tangential) motion and vertical motion due to gravity.
- The particle will leave the cylinder at point Q, which is directly below point P.
3. Vertical Motion Analysis:
- The vertical motion of the particle can be described using the equation of motion under gravity:
h=12gt2
- Rearranging this gives us the time t taken to fall a height h:
t=√2hg
4. Horizontal Motion Analysis:
- The horizontal distance traveled by the particle while it falls is determined by its initial horizontal speed v0:
Horizontal distance=v0⋅t
- Substituting the expression for t:
Horizontal distance=v0⋅√2hg
5. Circumference of the Cylinder:
- The circumference of the cylinder (the distance covered in one complete revolution) is given by:
C=2πR
6. Number of Revolutions:
- The number of revolutions n made by the particle can be calculated by dividing the horizontal distance by the circumference:
n=Horizontal distanceC=v0⋅√2hg2πR
- Simplifying this gives:
n=v02πR⋅√2hg
Final Result:
The number of revolutions made by the particle is:
n=v02πR⋅√2hg
- We have a hollow vertical cylinder with radius R and height h.
- A particle is placed at the top rim (point P) and given a horizontal speed v0 tangential to the rim.
- As the particle moves, it will experience two types of motion: horizontal (tangential) motion and vertical motion due to gravity.
- The particle will leave the cylinder at point Q, which is directly below point P.
- The vertical motion of the particle can be described using the equation of motion under gravity:
h=12gt2
- Rearranging this gives us the time t taken to fall a height h:
t=√2hg
- The horizontal distance traveled by the particle while it falls is determined by its initial horizontal speed v0:
Horizontal distance=v0⋅t
- Substituting the expression for t:
Horizontal distance=v0⋅√2hg
- The circumference of the cylinder (the distance covered in one complete revolution) is given by:
C=2πR
- The number of revolutions n made by the particle can be calculated by dividing the horizontal distance by the circumference:
n=Horizontal distanceC=v0⋅√2hg2πR
- Simplifying this gives:
n=v02πR⋅√2hg
The number of revolutions made by the particle is:
n=v02πR⋅√2hg
Topper's Solved these Questions
Similar Questions
A uniform ring of mass M and radius R=1m is placed horizontally on a frictionless horizontal surface. A particle of mass M2 is placed in contact with the inner side of ring as shown in the figure. What is the acceleration of the ring (in SI unit) just after the particle is given velocity v0=9m/s
tangentially to the ring?
 View Solution
View SolutionA hollow hemispherical bowl of mass m radius R is placed on a smooth horizontal surface. A particle (also of mass m) strikes the hemi spherical bowl at point P and sticks to it. the velocity of particle just after the collision in vertically upwards direction is ku25, where k is an integer. Find k.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A hollow vertical cylinder of radius R and height h has smooth internal suface. A small particle is placed in contact with the inner side of the upper rim at a point P. It is given a horizontal speed v0 tangential to rim. It leaves the lower rim point Q vertically below P. The number of revolutions made by the particle will:
Ah2πRBv0√2ghC2πRhDv02πR(√2hg) - Question 2 - Select One

A hollow vertical cylinder of radius r and height h has a smooth internal surface. A small particle is placed in contact with the inner side of the upper rim, at point A, and given a horizontal speed u, tangentical t the rim. it leaves the lower rim at point B, vertically below A. If n is an integer thenAu2πr√2h/g=nBh2πr=nC2πrh=nDu√2gh=n - Question 3 - Select One
In figure, a particle is placed at the highest point A of a smooth sphere of radius r. It is given slight push, and it leaves the sphere at B, at a depth h vertically below A. The value of h is
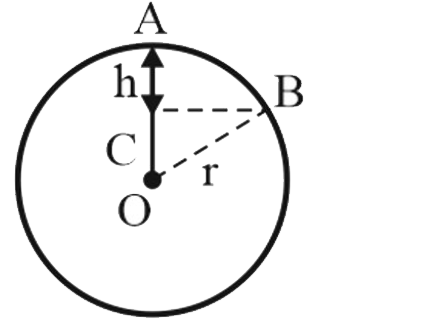 Ar6B14rC13rD12r
Ar6B14rC13rD12r
A particle of mass m and charge q is suspended from a point A with a silk thread of length l. Another particle of charge −q is fixes at a distance I from the point A such that point A and the charge -q lie in same horizontal plane. If at equilibrium , the thread makes angle 30∘ with vertical, find the mass m and tension in the thread . ( Take acceleration due to gravity as g).
View SolutionA uniformly conducting wire is bent to form a ring of mass 'm' and radius 'r', and the ring is placed on a rough horizontal surface with its plane horizontal. There exists a uniform and constant horizontal magnetic field of induction B. Now a charge q is passed through the ring in a very small time interval Δt. As a result the ring ultimately just becomes vertical. Calculate the value of g(acceleration due to gravity) in terms of other given quantities. Assume that friction is sufficient to prevent slipping and ignore any loss in energy.
View SolutionA cylinder of radius R=1m and height H=3m two- thirds filled with water, is rotated about its vertical axis as shown in Fig. Determine the speed of rotation when
a. the: water just starts spilling over the rim.
b. the point at the centre of the base is just exposed.
 View Solution
View SolutionA stone is projected horizontally with speed v from a height h above ground. A horizontal wind is blowing in direction opposite to velocity of projection and gives the stone a constant horizontal acceleration f( in direction opposite to initial velocity ) .As a result the stone falls on ground at a point vertically below the point of projection. Then the value of height h in terms of f,g,v is (g is acceleration due to gravity 0
View SolutionA particle of mass m moves along the internal smooth surface of a vertical cylinder of the radius R. Find the force with which the particle acts on the cylinder wall if at the initial moment of time its velocity equals v0. And forms an angle α with the horizontal.
View Solution

