A horizontal plane supports a fixed vertical cylinder of radius R and a particle is attached to the cylinder by a horizontal thread AB as shown in Fig. The particle initially rest on a horizontal plane. A horizontal velocity v0 is imparted to the particle, normal to the threading during subsequent motion. Point out the false statements:

angular momentum of particle about O remains constant
angular momentum about B remains constant
momentum and kinetic energy both remain constant
kinetic energy along remains constant
The correct Answer is:D
Step by step video & image solution for A horizontal plane supports a fixed vertical cylinder of radius R and a particle is attached to the cylinder by a horizontal thread AB as shown in Fig. The particle initially rest on a horizontal plane. A horizontal velocity v_(0) is imparted to the particle, normal to the threading during subsequent motion. Point out the false statements: by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A horizontal plane supports a stationary vertical cylinder of radius R and a disc A attached to the cylinder by a horizontal thread AB of length l0 (figure, to view). An initial velocity v0
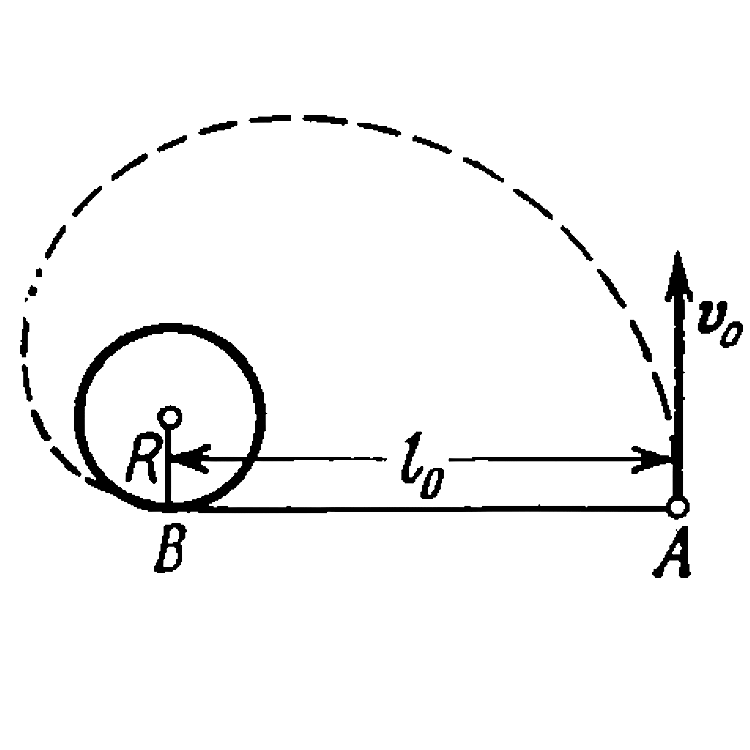
is imparted to the disc as shown in the figure. How long will it move along the plane until it strikes against the cylinder? The friction is assumed to be absent.
View SolutionOn a horizontal smooth plane there is a fixed vertical cylinder and a particle A connected to the cylinder by a thread AB. The particle is set in motion with the initial velocity v as shown in the figure. Is there any fixed point relative to which the angular

momentum of the particle is constant in the process of motion?
View Solution
Knowledge Check
A particle sides down from rest on an inclined plane of angle θ with horizontal. The distances are as shown. The particle slides down to the position A, where it velocity is v.
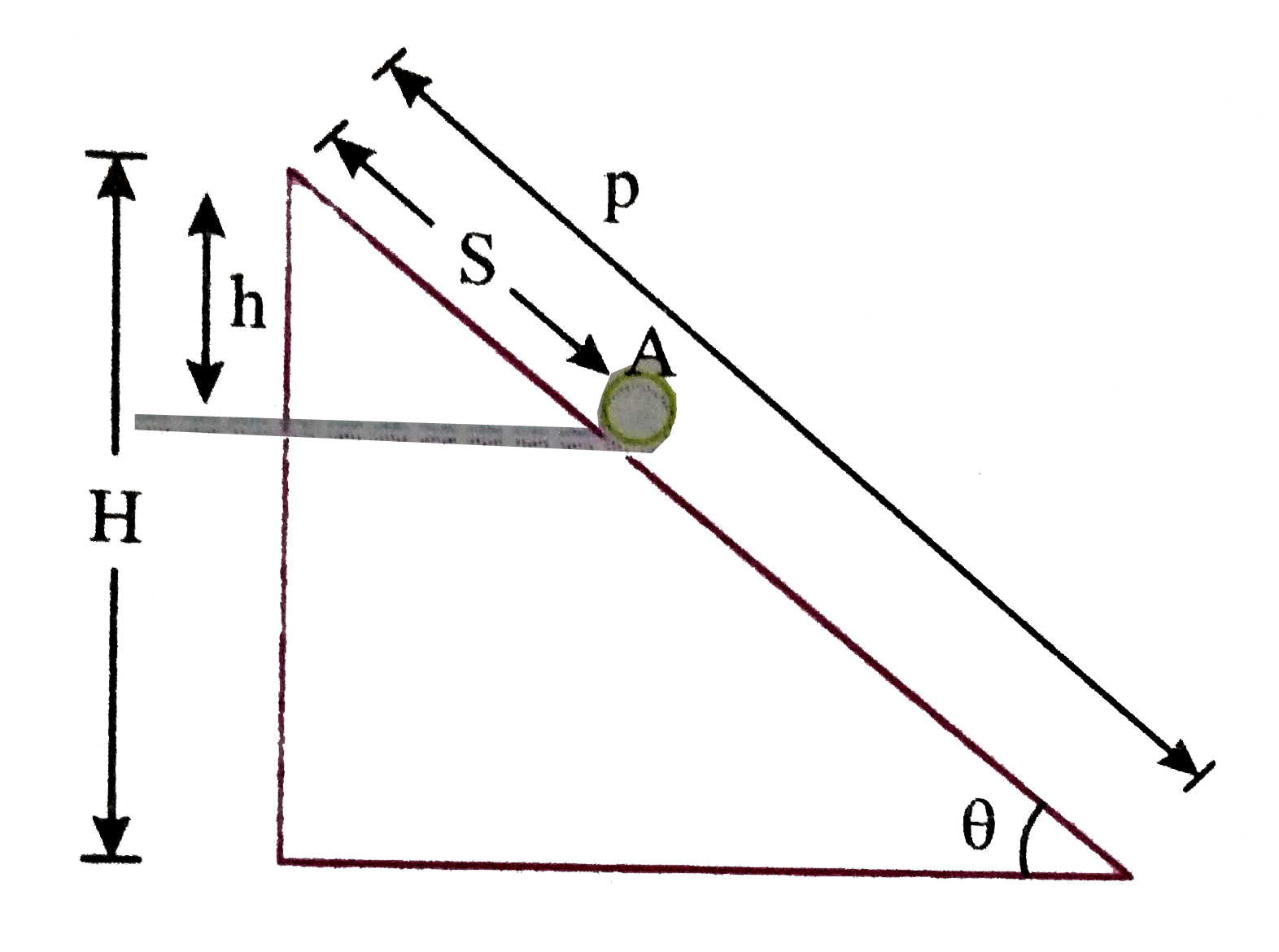 .A(v2−2gh) will remain zeroB(v2−2gssinθ) will remain zeroC[v2−2gs(H−h)(p−s)] will remain zeroD[v2−2gsHp] will remain zero.
.A(v2−2gh) will remain zeroB(v2−2gssinθ) will remain zeroC[v2−2gs(H−h)(p−s)] will remain zeroD[v2−2gsHp] will remain zero.Three identical particles are joined together by a thread as shown in figure. All the three particles are moving in a horizontal plane. If the velocity of the outermost particle is v0, then the ratio of tensions in the three sections of the string is (TBC:TAB:TDA)
 A3:5:7B3:4:5C7:11:6D3:5:6
A3:5:7B3:4:5C7:11:6D3:5:6A partcle rests on the top of a hemisphere of radius R. Find the smallest horizontal velocity that must be imparted to the particle if it is to leave the hemisphere without sliding down :
A√gRB√2gRC√3gRD√5gR
A particle is projected with velocity "u" in horizontal direction as shown in the figure. Find u if particle collides perpendicularly with inclined plane. h
View SolutionA light thread is tightly wrapped around a fixed disc of radius R. A particle of mass m is tied to the end P of the thread and the vertically hanging part of the string has length πR. The particle is imparted a horizontal velocity V=√4πgR3. The string wraps around the disc as the particle moves up. At the instant the velocity of the particle makes an angle of θ=60∘ with horizontal, calculate.
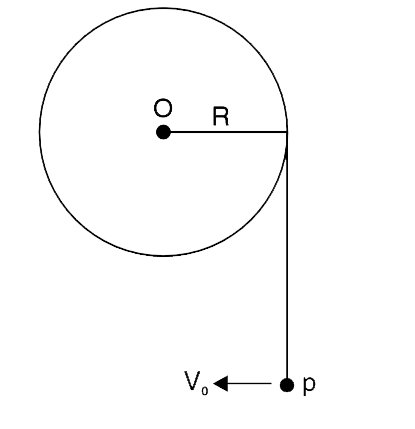
(a) Speed of the particle
(b) Tension in the string
View SolutionA partcle rests on the top of a hemisphere of radiu R. Find the smallest horizontal velocity that must be imparted to the particle if it is to leave the hemisphere without sliding down it-
View SolutionThree identical particles are joined together by a thread as shown in figure All the partical are moving in a horizontal plane If the vertical of the outermost particle is v0 then the ratio of tension in the three sections of the string (T1:T2:T3=?) is
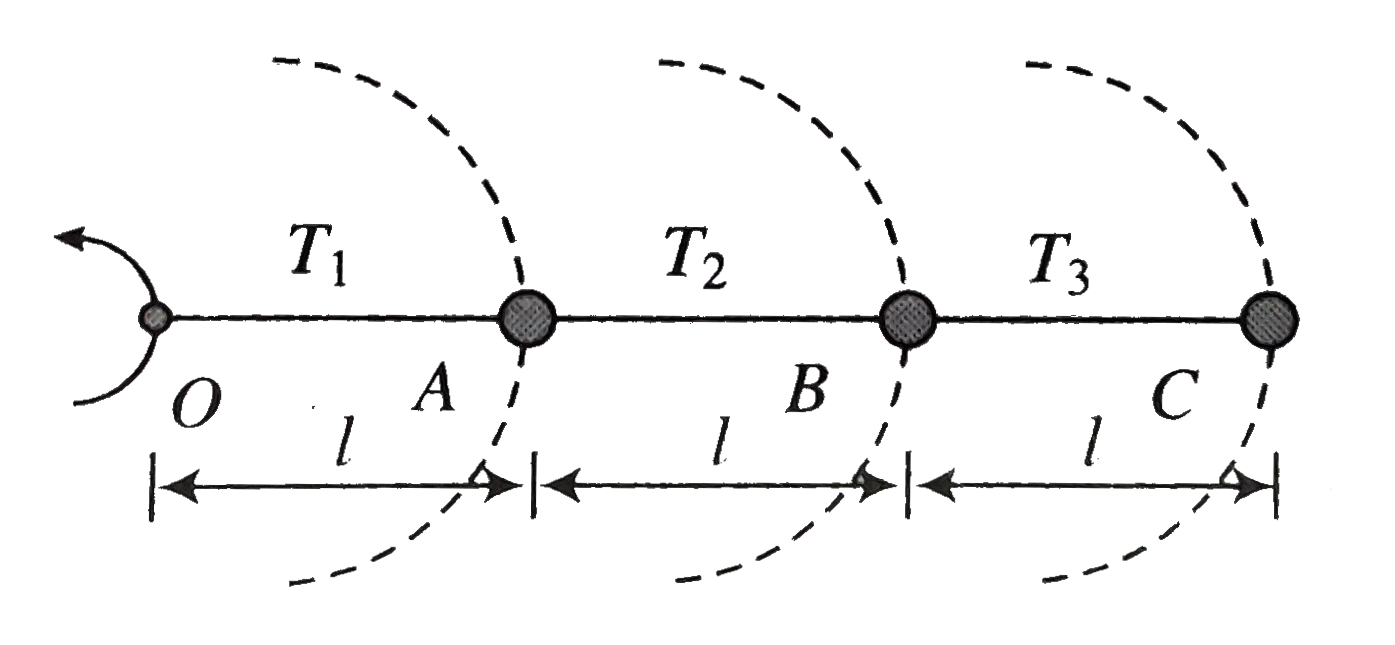
View SolutionIn figure, the angle of inclination of the inclined plane is 30∘. Find the horizontal velocity V0 so that the particle hits the inclined plane perpendicularly.
 .
.
View Solution
