A symmetrical uniform solid cube of side 5 m is placed on horizontal surface beside a vertical wall, one side of the cube is making an angle 45∘ with the floor as shown. If coefficient of friction μ is the same for both wall and floor, the minimum value of μ so that cube does not slip

μ=1
μ=0
μ=13
Impossible to balance for any value of μ
The correct Answer is:B
Step by step video & image solution for A symmetrical uniform solid cube of side 5 m is placed on horizontal surface beside a vertical wall, one side of the cube is making an angle 45^(@) with the floor as shown. If coefficient of friction mu is the same for both wall and floor, the minimum value of mu so that cube does not slip by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A uniform cube of mass m and side a is placed on a frictionless horizontal surface. A vertical force Fis applied to the edge as shown in figure. Match the following (most appropriate choice).

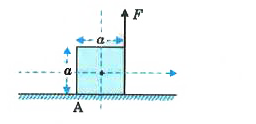
View SolutionA unifrom cube of mass m and side a is placed on a frictionless horizontal surface .A vertical force F is applied to the edge as shown in figure ,match the following (most appropriate choice )

View Solution
Knowledge Check
A ladder of length 5m is placed against a smooth wall as shown in figure. The coefficient or friction is μ between ladder and ground. What is the minimum value of μ , If the ladder is not to slip?
 Aμ=12Bμ=14Cμ=38Dμ=58
Aμ=12Bμ=14Cμ=38Dμ=58A homogeneous ball is placed on a plane making an angle θ with the horizontal. At what values of the coefficient of friction μ the ball roll down the plane without slipping ?
 .A≥27gtanθB≥25gtanθC≥23tanθD≥34tanθ
.A≥27gtanθB≥25gtanθC≥23tanθD≥34tanθA solid sphere of mass m is lying at rest on a rough horizontal surface. The coefficient of friction between the ground and sphere is μ. The maximum value of F, so that the sphere will not slip, is equal to
 A75μmgB47μmgC57μmgD72μmg
A75μmgB47μmgC57μmgD72μmg
(i) In the arrangement shown in the figure the coefficient of friction between the 2 kg block and the vertical wall is μ=0.5. A constant horizontal force of 40 N keeps the block pressed against the wall. The spring has a natural length of 1.0 m and its force constant is k=400Nm–1. What should be the height h of the block above the horizontal floor for it to be in equilibrium. The spring is not tied to the block.
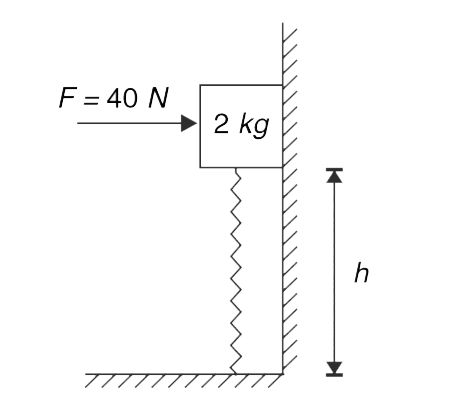
(ii) A block of mass M is pressed against a rough vertical wall by applying a force F making an angle of θ with horizontal (as shown in figure). Coefficient of friction between the wall and the block is μ=0.75.
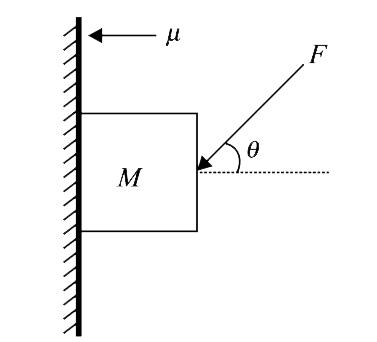
(a) If F = 2 Mg, find the range of values of θ so that the block does not slide
[Take tan37∘=0.75,sin24∘=0.4]
(b) Find the maximum value of θ above which equilibrium is not possible for any magnitude of force F.
View SolutionA block of mass m kg is pushed up against a wall by a force P that makes an angle 'θ' with the horizontal as shown in figure . The coefficient of static friction between the block and the wall is μ . Find the minimum value of P that allows the block to remain stationary .
View SolutionA block of mass m kg is pushed up against a wall by a force P That makes an angle 'theta' with the horizontal as shown in The coefficient of static friction between the block and the wall is μ The minimum value of P that allows the block to remain stationary is .
View SolutionA solid sphere of mass m is lying at rest on a rough horizontal surface. The coefficient of friction between the ground and sphere is μ. The maximum value of F, so that the sphere will not slip, is equal to

View SolutionIn Fig. 7.150 , coefficient of friction between m2 and the horizontal surface is μ , minimum value of m so that the system has zero acceleration , is :

View Solution
