A particle with linear momentum of magnitude P is subjected to a force F=Kt(K>0) which is directed along the direction of initial momentum. The time after which its linear momentum changes to 3P is
√2PK
2√PK
√2KP
2√2KP
The correct Answer is:B
To solve the problem, we will use the relationship between force, momentum, and time. The force acting on the particle is given as F=Kt, where K>0. We need to find the time t when the linear momentum changes from P to 3P.
1. Use Newton's Second Law:
According to Newton's second law, the force F is equal to the rate of change of momentum dpdt:
F=dpdt
2. Substitute the Given Force:
Substitute F=Kt into the equation:
Kt=dpdt
3. Rearranging the Equation:
Rearranging gives us:
dp=Ktdt
4. Integrate Both Sides:
We will integrate both sides. The left side will be integrated from the initial momentum P to the final momentum 3P, and the right side will be integrated from t=0 to t:
∫3PPdp=∫t0Ktdt
5. Calculate the Left Side:
The left side integrates to:
(p)3PP=3P−P=2P
6. Calculate the Right Side:
The right side integrates as follows:
∫t0Ktdt=K∫t0tdt=K(t22)t0=Kt22
7. Set the Integrals Equal:
Now we set the results of the integrals equal to each other:
2P=Kt22
8. Solve for t2:
Rearranging gives:
t2=4PK
9. Take the Square Root:
Taking the square root to find t:
t=√4PK=2√P√K
Final Answer:
The time after which the linear momentum changes to 3P is:
t=2√P√K
According to Newton's second law, the force F is equal to the rate of change of momentum dpdt:
F=dpdt
Substitute F=Kt into the equation:
Kt=dpdt
Rearranging gives us:
dp=Ktdt
We will integrate both sides. The left side will be integrated from the initial momentum P to the final momentum 3P, and the right side will be integrated from t=0 to t:
∫3PPdp=∫t0Ktdt
The left side integrates to:
(p)3PP=3P−P=2P
The right side integrates as follows:
∫t0Ktdt=K∫t0tdt=K(t22)t0=Kt22
Now we set the results of the integrals equal to each other:
2P=Kt22
Rearranging gives:
t2=4PK
Taking the square root to find t:
t=√4PK=2√P√K
The time after which the linear momentum changes to 3P is:
t=2√P√K
Topper's Solved these Questions
Similar Questions
If the net force acting upon the particle is zero, show that its linear momentum remains constant.
View SolutionA particle of mass is moving in a straight line with momentum p. Starting at time t= 0, a force F= kt acts in the same direction on the moving particle during time interval T so that its momentum changes from p to 3p. Here k is constant . The value of T is :
View Solution
Knowledge Check
For a given change in linear momentum when time of impact increases force .
AdecreasesBincreasesCremains sameDnone of the aboveThe linear momentum of a particle varies with time t as p=a+bt+ct2. Then, whichh of the following is correct?
AVelocity of particle is inversely proportional to timeBDisplacement of the particle is independent of timeCForces varies with time in a quadratic mannerDForce is independent linearly on timeA body of massm is moving in a straight line with momentum p. Starting at time t = 0, a force F = at acts in the same direction on the moving particle during time interval of T. So that its momentum changes from p to 2p. The value of T is
A√2paB√paC√2paD2pa
A force-time graph for the motion of a body is shown in fig. Change in linear momentum between 0 and 8s is :
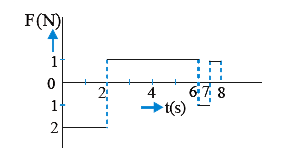
View SolutionA force-time graph for the motion of a body is shown in fig. change in linear momentum between 0 and 8 s is:-
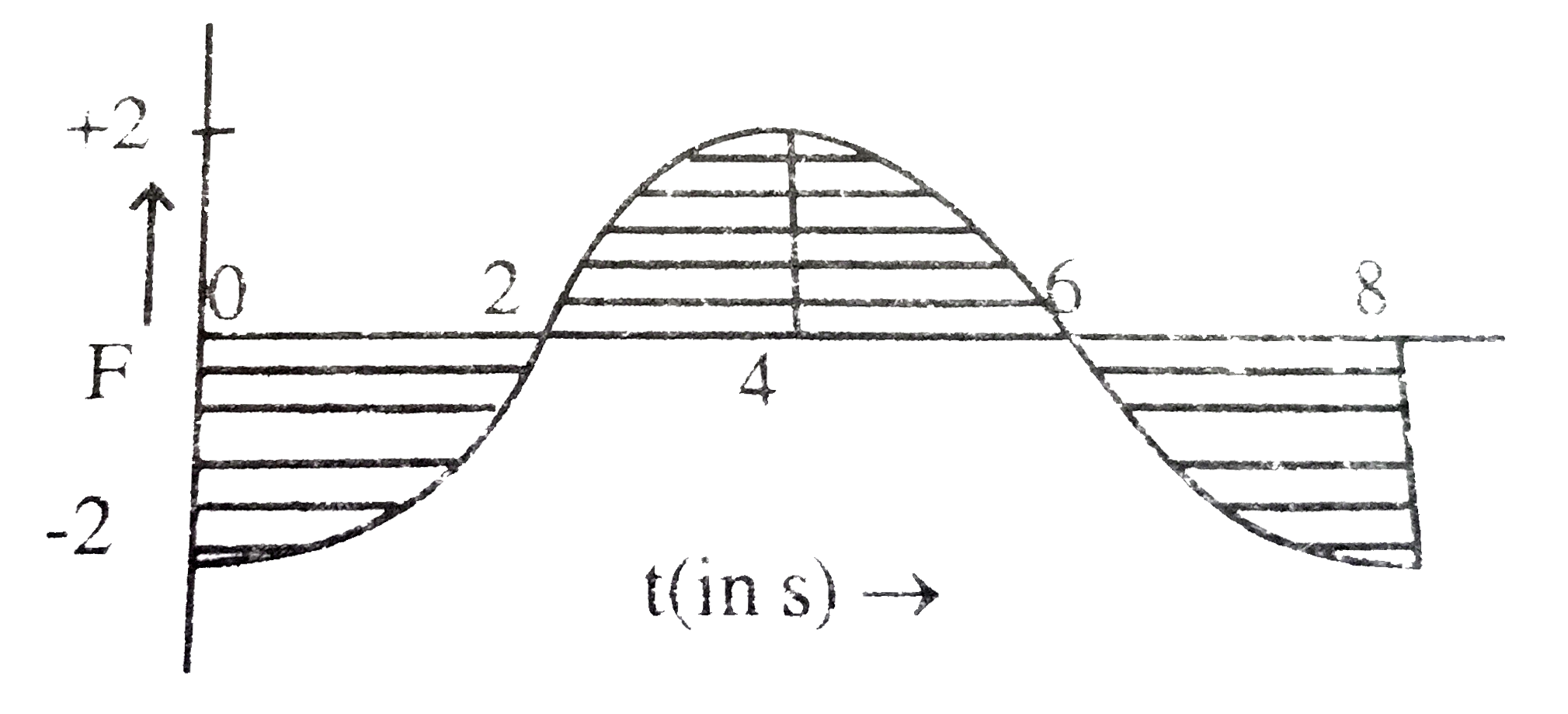
View SolutionIF p is the magnitude of linear momentum of a particle executing a uniform circular motion, then the ratio of centripetal force acting on the particle to its linear momentum is given by
View SolutionA particle is moving with momentum P and kinetic K in a gravity free space. A constant force F (directed perpendicular to the initial momentum) now acts on the particle for time t. Final kinetic energy of the particle will be
View SolutionA force-time graph for the motion of a body is shown in figure. Change in linear momentum between 0 and 8 s is:

View Solution
