A particle strikes elastically with another particle with velocity V after collision its move with half the velocity in the same direction find the velocity of the second particle if it is initially at rest
V
none of these
The correct Answer is:A
To solve the problem step by step, we need to apply the principles of conservation of momentum and the characteristics of elastic collisions.
1. Understand the Problem:
- We have two particles.
- Particle 1 (P1) is moving with an initial velocity V.
- Particle 2 (P2) is initially at rest (velocity = 0).
- After the elastic collision, P1 moves with a velocity of V2.
2. Define the Variables:
- Let V1 be the initial velocity of P1 = V.
- Let V2 be the initial velocity of P2 = 0.
- Let V′1 be the final velocity of P1 after the collision = V2.
- Let V′2 be the final velocity of P2 after the collision (which we need to find).
3. Apply Conservation of Momentum:
The total momentum before the collision must equal the total momentum after the collision.
Initial Momentum=Final Momentum
m1V1+m2V2=m1V′1+m2V′2
Assuming both particles have the same mass m:
mV+0=m(V2)+mV′2
Simplifying, we get:
V=V2+V′2
4. Solve for V′2:
Rearranging the equation gives:
V′2=V−V2
V′2=V2
5. Use the Elastic Collision Equation:
For an elastic collision, the relative velocity of separation is equal to the relative velocity of approach:
V′2−V′1=V1−V2
Substituting the known values:
V′2−V2=V−0
V′2−V2=V
Rearranging gives:
V′2=V+V2=3V2
6. Conclusion:
The final velocity of the second particle (P2) after the collision is 3V2.
Final Answer:
The velocity of the second particle after the collision is 3V2.
---
- We have two particles.
- Particle 1 (P1) is moving with an initial velocity V.
- Particle 2 (P2) is initially at rest (velocity = 0).
- After the elastic collision, P1 moves with a velocity of V2.
- Let V1 be the initial velocity of P1 = V.
- Let V2 be the initial velocity of P2 = 0.
- Let V′1 be the final velocity of P1 after the collision = V2.
- Let V′2 be the final velocity of P2 after the collision (which we need to find).
The total momentum before the collision must equal the total momentum after the collision.
Initial Momentum=Final Momentum
m1V1+m2V2=m1V′1+m2V′2
Assuming both particles have the same mass m:
mV+0=m(V2)+mV′2
Simplifying, we get:
V=V2+V′2
Rearranging the equation gives:
V′2=V−V2
V′2=V2
For an elastic collision, the relative velocity of separation is equal to the relative velocity of approach:
V′2−V′1=V1−V2
Substituting the known values:
V′2−V2=V−0
V′2−V2=V
Rearranging gives:
V′2=V+V2=3V2
The final velocity of the second particle (P2) after the collision is 3V2.
The velocity of the second particle after the collision is 3V2.
Topper's Solved these Questions
Similar Questions
A particle of mass m1 moves with velocity v1 and collides with another particle at rest of equal mass. The velocity of the second particle after the elastic collision is
View SolutionA particle of mass m strikes elastically with a disc of radius R, with a velocity →v as shown in the figure. If the mass of the disc is equal to that of the particle and the surface of the contact is smooth, find the velocity of the disc just after the collision.

View Solution
Knowledge Check
A sphere of mass m moves with a velocity 2v and collides inelastically with another identical sphere of mass m. After collision the first mass moves with velocity v in a direction perpendicular to the initial direction of motion . Find the speed of the second sphere after collision .
AvBv√5C2√3vDv√3A mass m moves with a velocity v and collides inelastically with another identical mass at rest. After collision, the first mass moves with velocity v√3 in a direction perpendicular to Before collision the initial direction of motion. The speed of the 2nd mass after collision
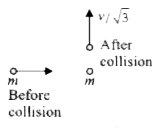 A2v√3Bv√3CvD√3v
A2v√3Bv√3CvD√3vTwo particle moving in the same direction with speeds 4m/s and 2m/s collide elastically (the collision being head on). After collision , the velocity of first particle becomes 3m/s in the same direction . The velocity of the second should be
A2m/s in same directionB4m/s in same directionC4m/s in opposite directionD5m/s in same direction
A particle of mass 2kg moving with a velocity 5ˆim/s collides head-on with another particle of mass 3kg moving with a velocity −2ˆim/s. After the collision the first particle has speed of 1.6m/s in negative x-direction, Find
(a) velocity of the centre of mass after the collision,
(b) velocity of the second particle after the collision.
(c) coefficient of restitution.
View SolutionA mass ‘m’ moves with a velocity ‘v’ and collides inelastically with another identical mass at rest. After collision the 1st mass moves with velocity v√3 in a direction perpendicular to the initial direction of motion. Find the speed of the 2nd mass after collision :
View SolutionA particle of mass m moving with velocity →V makes a head on elastic collision with another particle of same mass initially at rest. The velocity of the first particle after the collision will be
View SolutionA particle of mass m moving with velocity →V makes a head on elastic collision with another particle of same mass initially at rest. The velocity of the first particle after the collision will be
View SolutionA particle starts from rest with uniform acceleration a. Its velocity after n seconds is v. The displacement of the particle in the two seconds is :
View Solution
