A small sphere is given vertical velocity of magnitude v0=5ms−1 and it swings in a vertical plane about the end of a massless string. The angle θ with the vertical at which string will break, knowing that it can withstand a maximum tension equal to twice the weight of the sphere, is
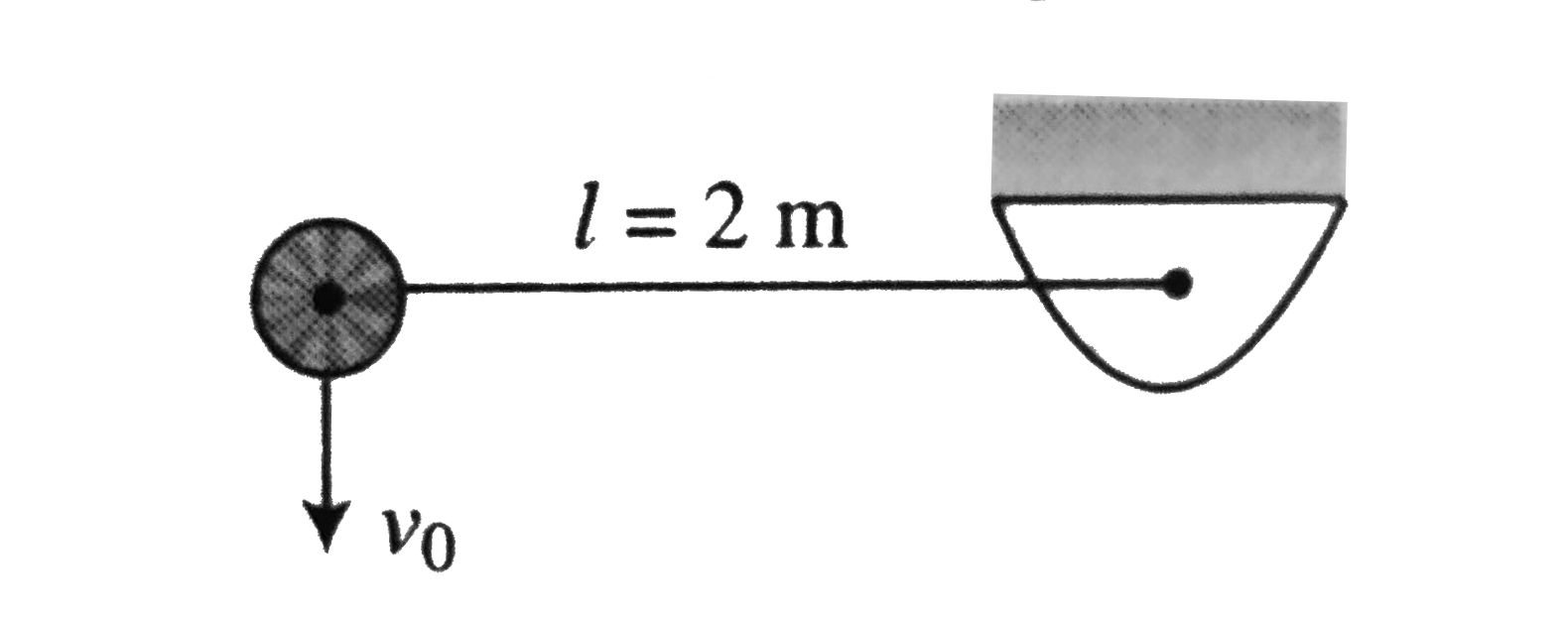
cos−1(23)
cos−1(14)
60∘
30∘
The correct Answer is:B
Step by step video & image solution for A small sphere is given vertical velocity of magnitude v_0=5ms^-1 and it swings in a vertical plane about the end of a massless string. The angle theta with the vertical at which string will break, knowing that it can withstand a maximum tension equal to twice the weight of the sphere, is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The sphere at A is given a downward velocity v0 of magnitude 5m/s and swings in a vertical plane at the end of a rope of length l=2m attached to a support at O . Determine the angle θ at which the rope will breack, knowing that it can withstant a maximum tension equal to twich the weight of the sphere.
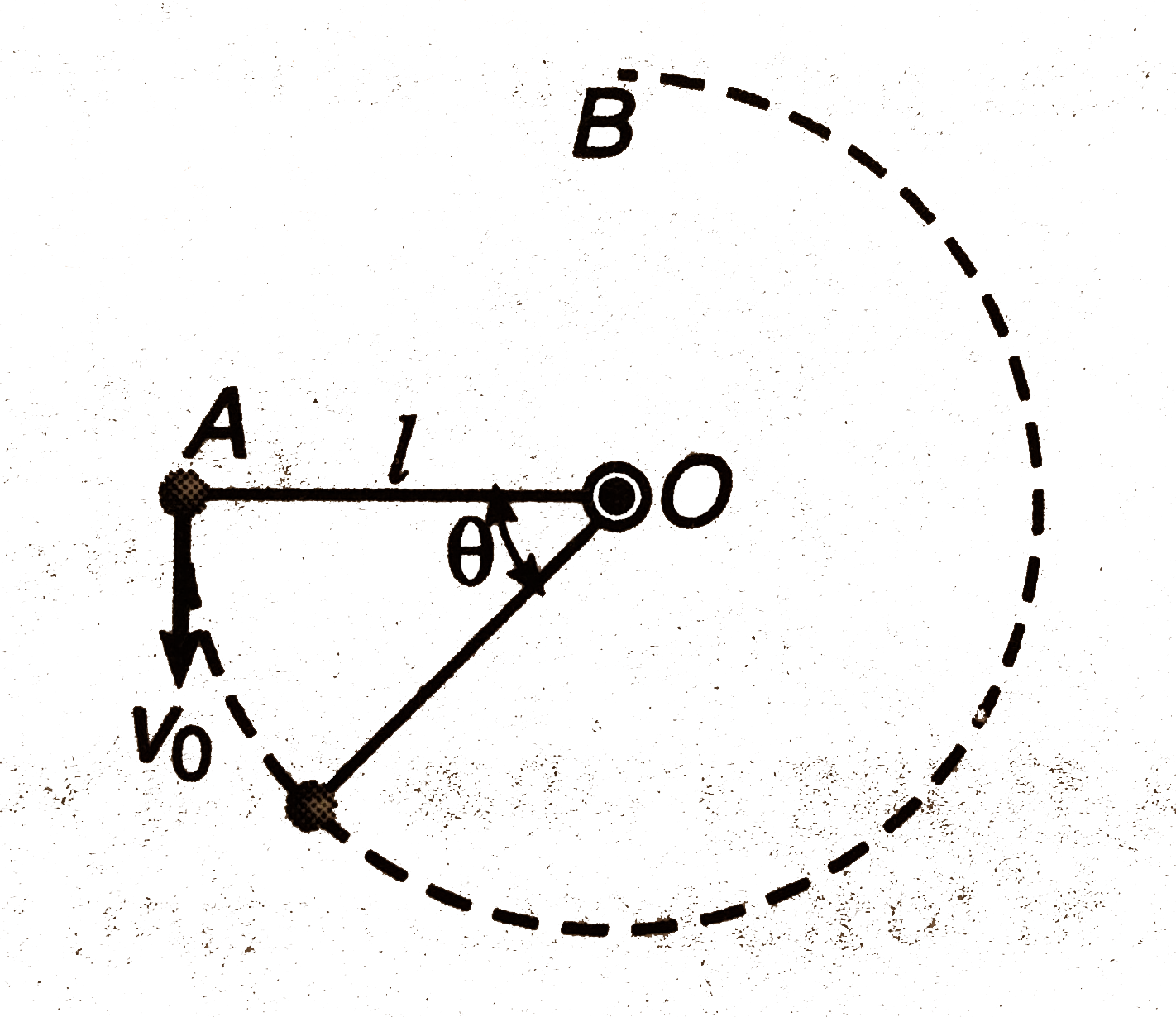
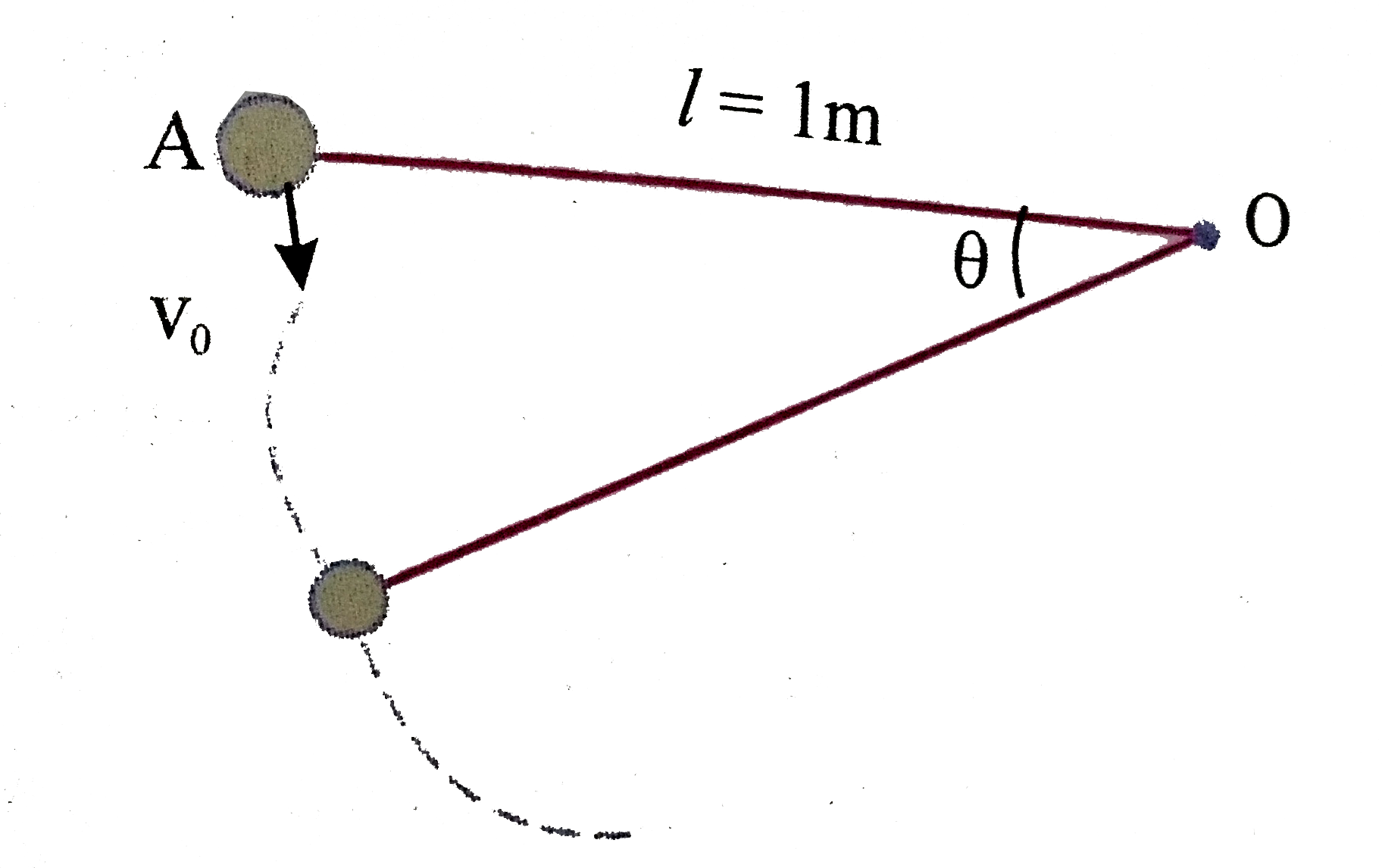
View SolutionThe sphere at P is given a down ward velocity v0 and swings in a vertical plane at the end of a rope of l=1m attached to a support at O. The rope breaks at angle 30∘ from horizontal, knowing that it can withstand a maximum tension equal to four times the weight of the sphere. then the value of v0 will be (g=10m/s2).
 .
.
View Solution
Knowledge Check
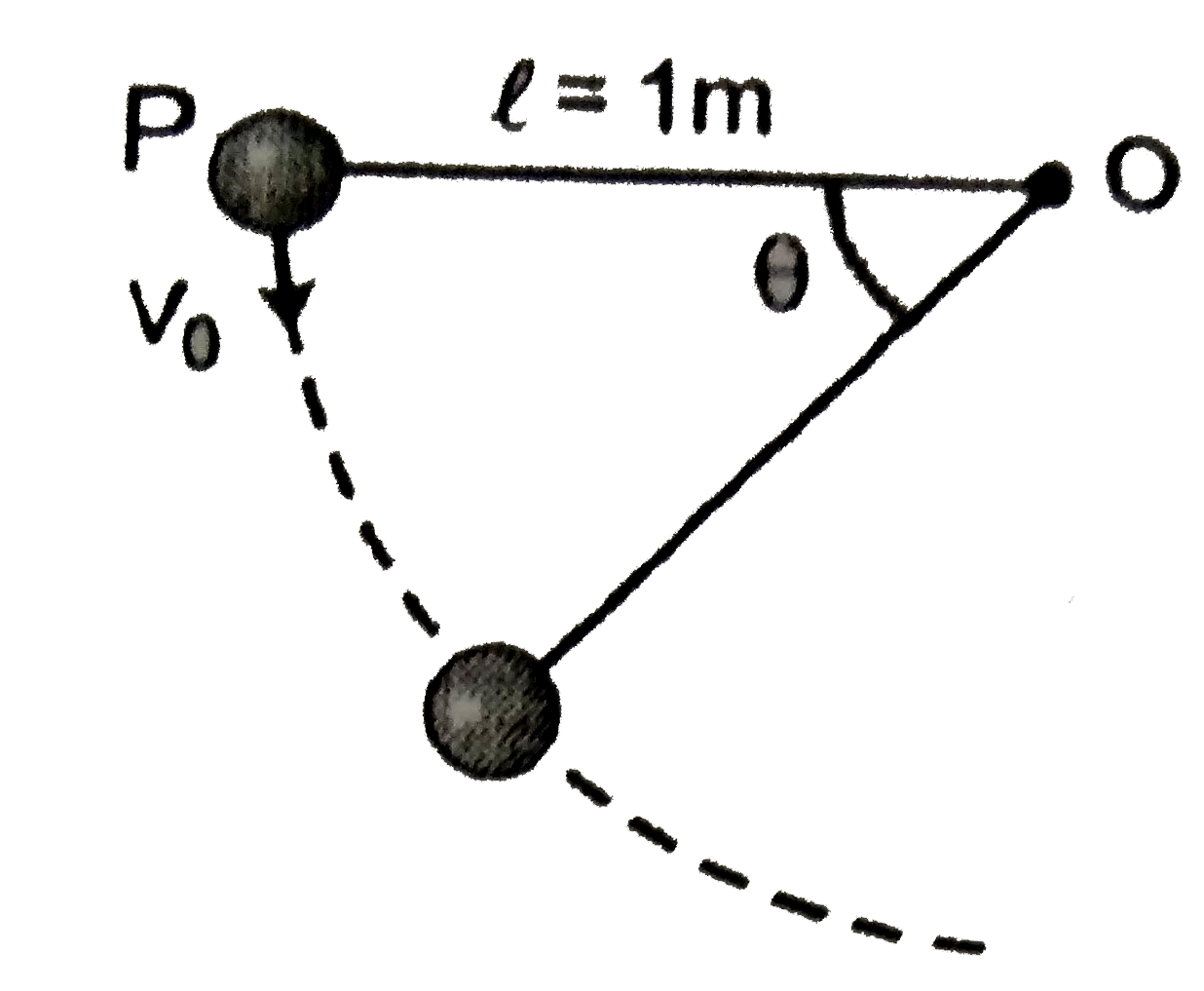
The sphere at P is given a downward velocity v0 and swings in a vertical plane at the end of a rope of l=1m attached to a support at O. The rope breaks at angle 30∘ from horizontal , knowing that it can withstand a maximum tension equal to three times the weight of the sphere. Then the value of v0 will be :
(g=π2m/s2)
 Ag2m/sB2g3m/sC√3g2m/sDwill have minimum value 38m
Ag2m/sB2g3m/sC√3g2m/sDwill have minimum value 38mA simple pendulum of length L swings in a vertical plane. The tension of the string when it makes an angle θ with the vertical and the bob of mass m moves with a speed v is (g is the gravitational acceleration)
Amv2/LBmgcosθ+mv2/LCmgcosθ−mv2/LDmgcosθA body of mass 2kg attached at one end of light string rotated along a vertical circle of radius 2m. If the string can withstand a maximum tension of 140.6N, the maximum speed with which the stone can be rotated is
A22m/sB44m/sC33m/sD11m/s
A 4 kg balls is swing in a vertical circle at the end of a cord 1 m long. The maximum speed at which it can swing if the cord can sustain maximum tension of 163.6 N will be
View SolutionA stone is attached to one end of a string and rotated in a vertical circle . If the string breaks at the position of maximum tension , then it will break at
View SolutionA bob tied to the end of a string of length 2m, other end of which is fixed at a point in a vertical wall at a point O. The bob is imparted a vertical downward velocity of 5m/s when the string is horizontal and swings in a vertical plane. Find the angular displacement of the bob from its initial position, when the string breaks. Given that the tensile strength of the string is twice the weight of the bob. Take g=10m/s2
View SolutionA small body tied to one end of the string is whirled in a vertical circle. Represent the forces on a diagram when the string makes an angle θ with initial position.
View SolutionA simple pendulum has a bob of mass m and swings with an angular amplitude ϕ. The tension in thread is T. At a certain time the string makes an angle θ with the vertical (θ≤ϕ)
View Solution
