Consider the earth as a uniform sphere if mass M and radius R. Imagine a straight smooth tunnel made through the earth which connects any two points on its aurface. Show that the motion of a particle of mass m along this tunnel under the action of gravitation would be simple harmonic. Hence, determine the time that a particle would take to go from one end to the other through the tunnel.
2π√R3GM
π√R3GM
π2√R3GM
None of these
The correct Answer is:B
Step by step video, text & image solution for Consider the earth as a uniform sphere if mass M and radius R. Imagine a straight smooth tunnel made through the earth which connects any two points on its aurface. Show that the motion of a particle of mass m along this tunnel under the action of gravitation would be simple harmonic. Hence, determine the time that a particle would take to go from one end to the other through the tunnel. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Two particles of equal mass go round a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.
View SolutionTwo particles of equal mass (m) move in a circle of radius (r ) under the action of their mutual gravitational attraction. Find the speed of each particle.
View Solution
Knowledge Check
Four particles each of mass M move along a circle of radius R under the action of their mutula gravitational attraction the speed of each paritcles is
AGmRB√2√2GMRC√GMR(2√2+1)D√GMR2√2+14Two particles of same mass m go around a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is ,
AV=12R√1GmBV=√GM2RCV=12√GmRDV=√4GmRFour particles each of mass M move along a circle of radius R under the action of their mutula gravitational attraction the speed of each paritcles is
A√GMRB√2√2GMRC√GMR(1+2√2)D12√GMR(1+2√2)
Two particles each of equal mass (m) move along a circle of radius (r) under the action of their mutual dravitational. Find the speed of each particle.

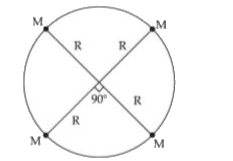
View SolutionFour particles each of mass M, move along a circle of radius R under the action of their mutual gravitational attraction as shown in figure. The speed of each particle is :
View SolutionTwo particles of equal mass go around a circle of radius R under the action of their mutual gravitational attraction. The speed v of earth particle is
View SolutionImagine a narrow tunnel between the two diametrically opposite points of the earth. A particle of mass m is released in this tunnel . The time period of oscillation is
View SolutionTwo particles of equal mass m go around a circle of radius R under the action the of their mutual gravitational attraction . The speed v of each particle is
View Solution
