Question

Terminal velocity $\left(V\right)$ of a spherical object varies with a radius of object $\left(r\right)$ -

Options

A.
B.
C.
D.

Answer

A

Explanation

To solve the problem regarding the relationship between terminal velocity (V) and the radius (r) of a spherical object, we can follow these steps:

1. Understanding Terminal Velocity:
Terminal velocity is the constant speed that a freely falling object eventually reaches when the resistance of the medium prevents further acceleration. For a spherical object falling through a viscous medium, the forces acting on it are the gravitational force (downward) and the drag force (upward).

2. Forces Acting on the Object:
- The gravitational force acting on the object is given by \( F_g = mg \), where \( m \) is the mass of the object and \( g \) is the acceleration due to gravity.
- The drag force acting on the object can be expressed as \( F_d = 6 \pi \eta r V \), where \( \eta \) is the coefficient of viscosity, \( r \) is the radius of the spherical object, and \( V \) is the terminal velocity.

3. Setting Up the Equation:
At terminal velocity, the drag force equals the gravitational force:
\( mg = 6 \pi \eta r V \)

4. Expressing Mass in Terms of Density:
The mass \( m \) can be expressed in terms of the density of the object \( \rho \) and its volume. The volume \( V \) of a sphere is given by \( V = \frac{4}{3} \pi r^3 \), so:
\( m = \rho \cdot V = \rho \cdot \frac{4}{3} \pi r^3 \)

5. Substituting Mass into the Equation:
Substituting \( m \) into the force balance equation gives:
\( \rho \cdot \frac{4}{3} \pi r^3 g = 6 \pi \eta r V \)

6. Simplifying the Equation:
Canceling \( \pi \) from both sides and rearranging gives:
\( \frac{4}{3} \rho r^2 g = 6 \eta V \)
\( V = \frac{2}{9} \frac{\rho g r^2}{\eta} \)

7. Identifying the Relationship:
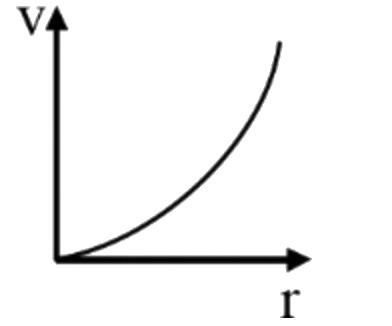
From the final equation, we can see that terminal velocity \( V \) is proportional to the square of the radius \( r \):
\( V \propto r^2 \)

8. Graphical Representation:
The relationship \( V \propto r^2 \) indicates that if we were to plot terminal velocity \( V \) against radius \( r \), the graph would be a parabola opening upwards. However, since the radius cannot be negative, the graph will only exist in the first quadrant.

Conclusion:
The terminal velocity \( V \) of a spherical object varies with the square of its radius \( r \) as \( V \propto r^2 \).