Statement - 1 Let ABCD and BEFG are two parallelograms such that E lies on AD and C lies on FG then ar(ABCD)ar(BEFG)=1
Statement - 2, ar(ABCD) =12ar(ΔBEC) = ar (BEFG)
Statement - 1 is True, statement -2 is true, statement-2 is a correct explanation fro statement - 1
Statement - 1 is True. Statement - 2 is true statement -2 is Not a correct explanation for statement -1
Statement -1 is True, statement -2 is False
Statement -1 is False, Statement -2 is True
The correct Answer is:A
Topper's Solved these Questions
- AREABOOK - FIITJEECHAPTER - AREAEXERCISE - Assignment Problems (Objective) Level - II
20 Videos
- AREABOOK - FIITJEECHAPTER - AREAEXERCISE - Comprehensions
9 Videos
- AREABOOK - FIITJEECHAPTER - AREAEXERCISE - Exercuse 4
4 Videos
- APPLICATION OF DERIVATIVEBOOK - FIITJEECHAPTER - APPLICATION OF DERIVATIVEEXERCISE - Numerical
3 Videos
- CIRCLEBOOK - FIITJEECHAPTER - CIRCLEEXERCISE - Numerical Based
2 Videos
Similar Questions
Knowledge Check
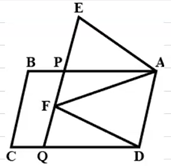
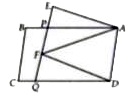
In the given figure, ABCD and AEFD a re two parallelograms.
ar(ΔPEA) =Aar(∣∣gmΔPEA)Bar(ΔPFD)Car(ΔQFD)Dar(∣∣gmΔCQPB)In the figure, ABCD and EFGD are two parallelograms and G is the mid-point of CD. Then, ar(ΔDPC)=ar(EFGD).
 ATrueBFalseCPartially trueDNone of these
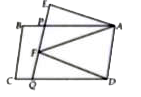
ATrueBFalseCPartially trueDNone of theseIn the given figure, ABCD and AEFD a re two parallelograms.
(ar(ΔAPE))/(ar(ΔPFA)) =A(ar(ΔQFD))/(ar(ΔPFD))B(ar(ΔAEF))/(ar(ΔPFD))C(ar(ΔQFD))/(ar(ΔAEF))DNone of these
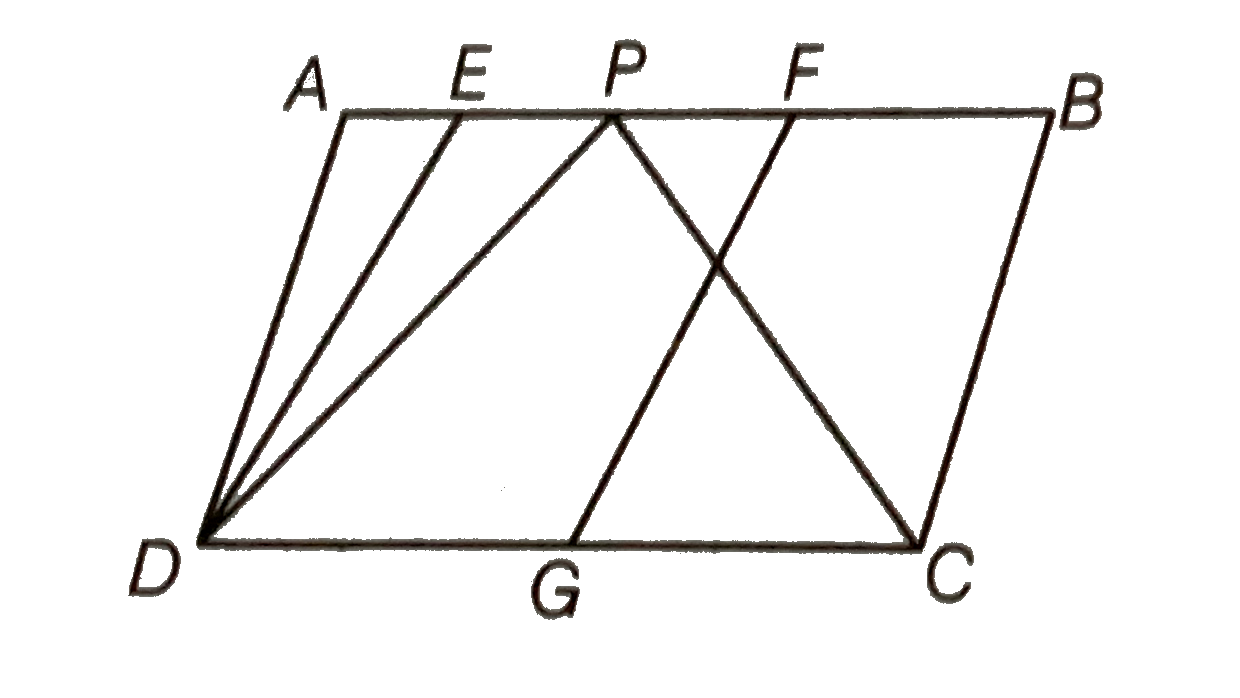
In figure, ABCD and AEFD are two parallelograms. Prove that ar(ΔPEA)=ar(ΔQFD).
View SolutionIn the figure, ABCD, DCFE and ABFE are parallelograms. Show that ar(ΔADE) = ar(ΔBCF).
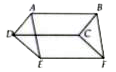
View SolutionIn Fig. 9.31, ABCD, DCFE and ABFE are parallelograms. Show that ar(ADE)=ar(BCF).
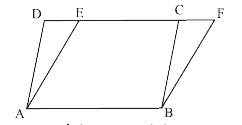
View SolutionIn the figure ABCD and ABFE are Parallelograms then find ar (ΔBCF).
If ar (ABCE)=18cm2
ar (ABCD)=25cm2
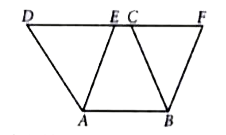
View SolutionIn the given figure, ABCD and ABFE are parallelograms such that ar(quad. EABC) =19 cm2 and ar(||gm ABCD) = 28 cm2. Then, ar(△BCF) is
View Solution