In figure, ABCD and AEFD are two parallelograms. Prove that ar(ΔPEA)=ar(ΔQFD).
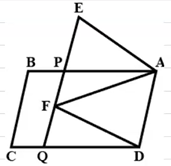
Given, ABCD and AEFD are two parallelograms.
To prove ar(ΔPEA)=ar(ΔQFD)
Proof In quadrilateral PQDA,
AP∣∣DQ [since, in parallelogram ABCD, AB∣∣CD]
and PQ∣∣AD [since, in parallelogram AEFD, FE∣∣AD]
Then, quadrilateral PQDA is a parallelogram.
Also, parallelogram PQDA and AEFD are on the same base AD and between the same parallels AD and EQ.
∴ ar (parallelogram PQDA) = ar (parallelogram AEFD)
On subtracting ar (quadrilateral APFD) from both sides, we get
ar (parallelogram PQDA)- ar (quadrilateral APFD)
= ar (parallelogram AEFD) - ar (quadrilateral APFD)
⇒ ar(ΔQFD)=ar(ΔPEA) Hence proved.
Topper's Solved these Questions
Similar Questions
In the adjoining figure, ABCD and PBCQ are parallelogram. Prove that:

ΔABP≅ΔDCQView SolutionIn the adjoining figure, ABCD and PBCQ are parallelogram. Prove that:

AP= DQView SolutionIn the adjoning figure, ABCD is a parallelogram. Prove that : area of ΔBPC= area of ΔDPQ
 View Solution
View SolutionIn the given figure ABCD is a parallelogram. Prove that AB = 2BC.
 View Solution
View SolutionIn the figure, the area of parallelogram ABCD is
 View Solution
View SolutionIn figure, ABCD and AEFG are two parallelograms. If ∠C=55∘, then determine ∠F.
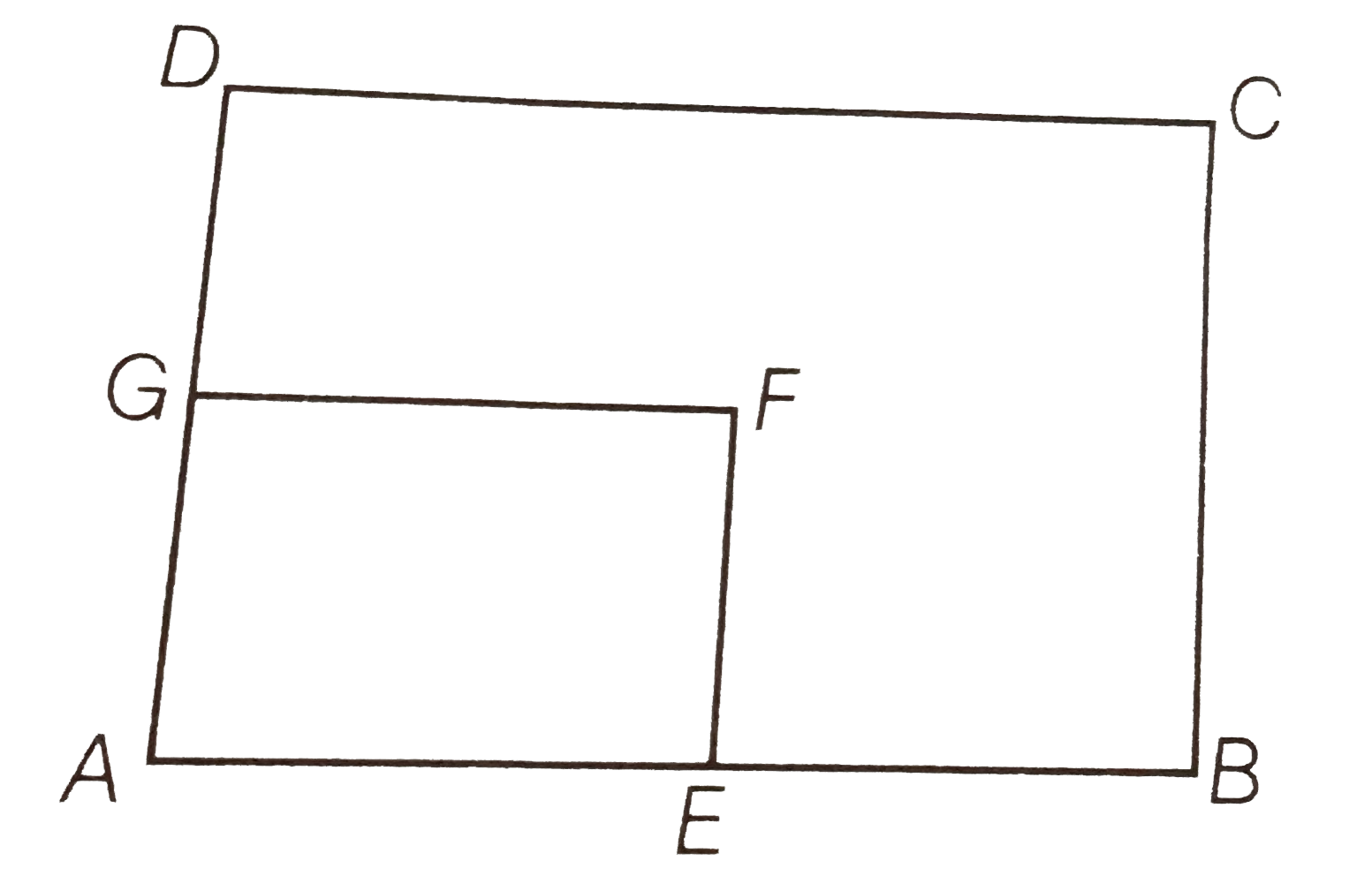 View Solution
View SolutionIn the given figure, ABCD and FECG are parallelograms equal in area. If ar(ΔAQE)=12cm2, find ar(∣∣gmFGBQ)
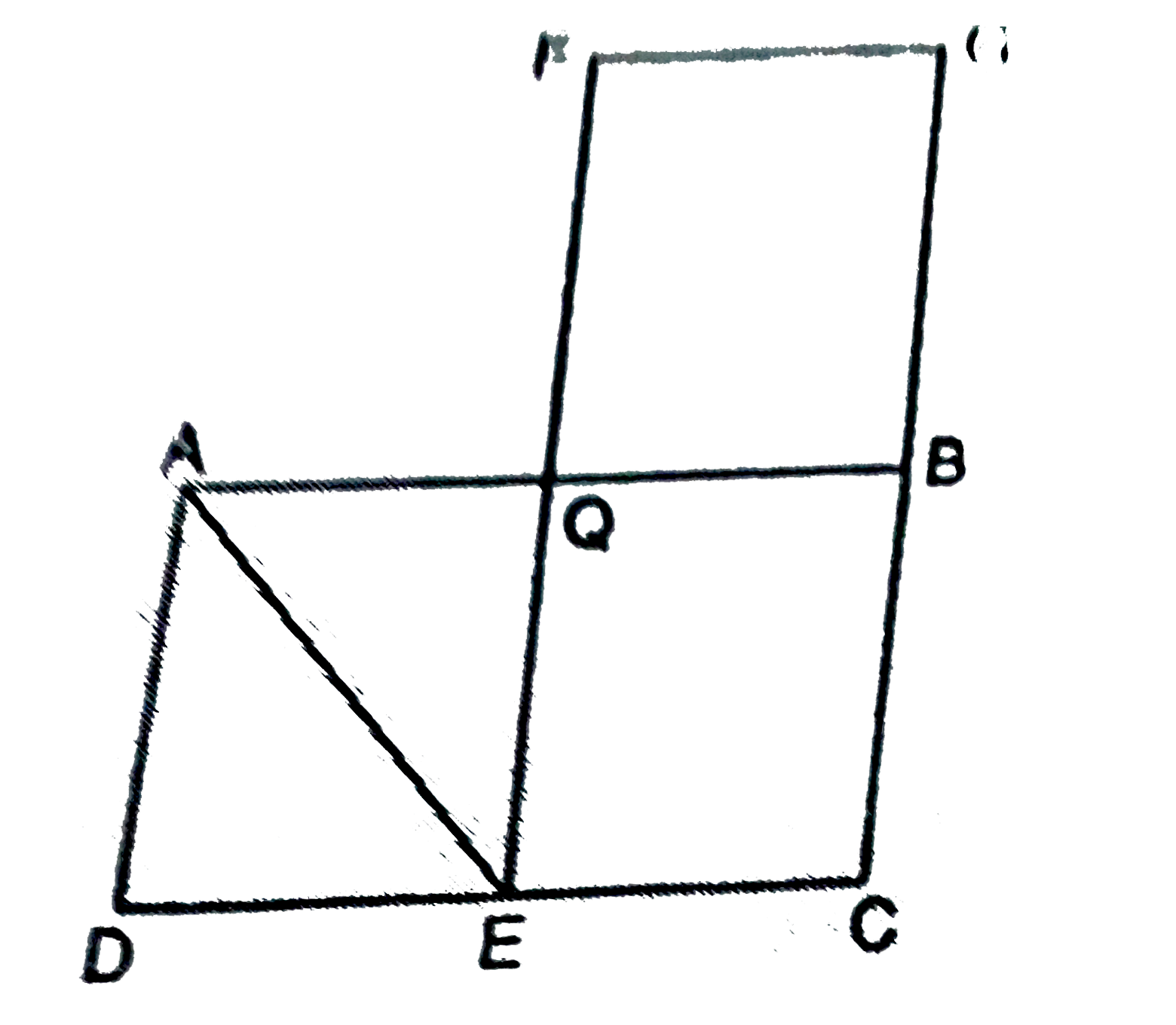 View Solution
View SolutionO is any point on the diagonal PR of a parallelogram PQRS (figure). Prove that ar(ΔPSO)=ar(ΔPQO).
 View Solution
View SolutionIn the given figure, ABCD is a parallelogram. Find the area of ΔAED
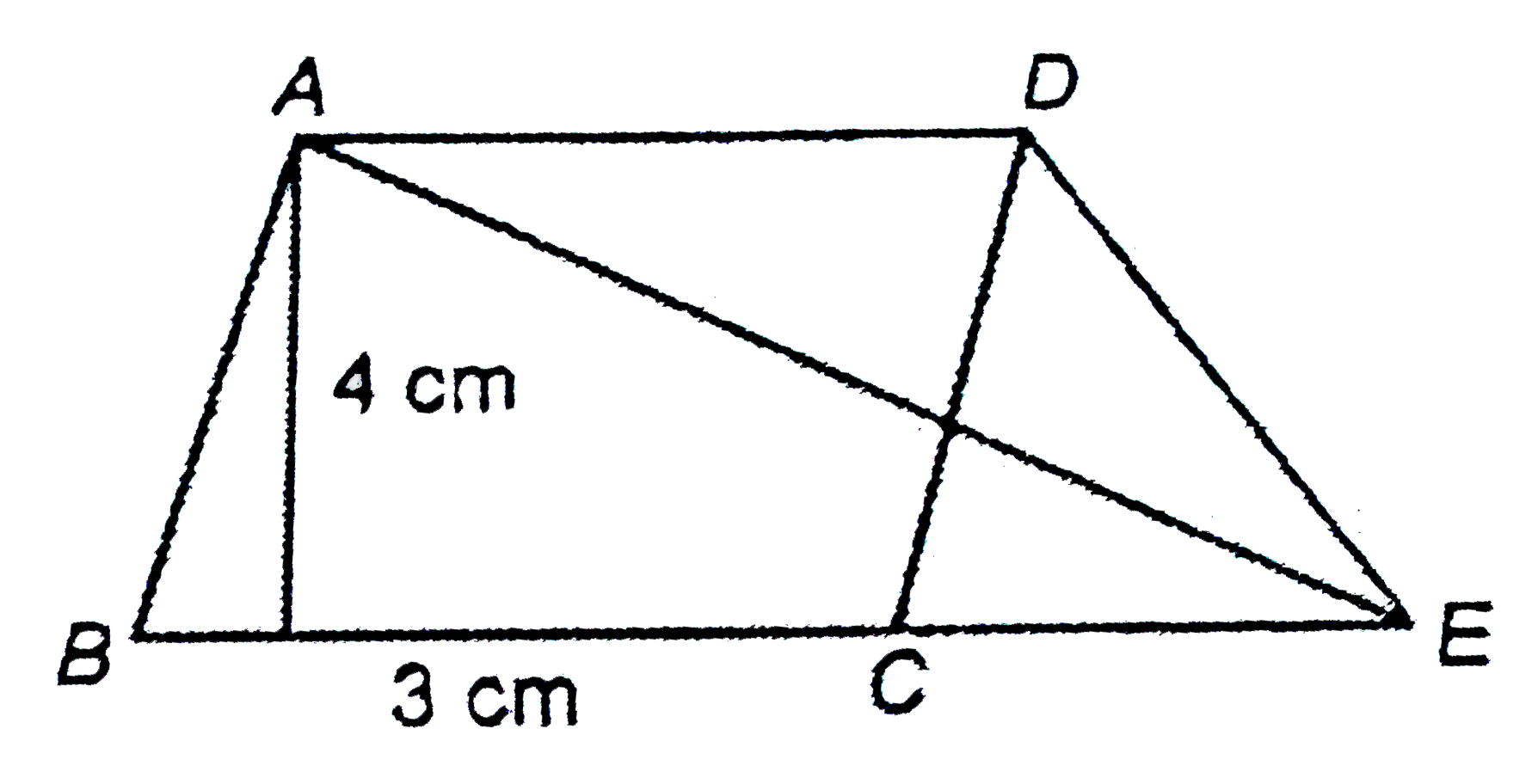 View Solution
View SolutionIn figure X and Y are the mid-points of AC and AB respectively, QP∣∣BC and CYQ and BXP are straight lines. Prove that ar(ΔABP)=ar(ΔACQ).
 View Solution
View Solution

