The value of cot[cos−1(725)] is
A
2524
B
257
C
2425
D
724
Video Solution
Text Solution
The correct Answer is:D
We have, cot[cos−1(725)]
Let cos−1'725=x
⇒cosx=725
∴sinx=√1−cos2x=√1−(725)2
=√625−49625=2425
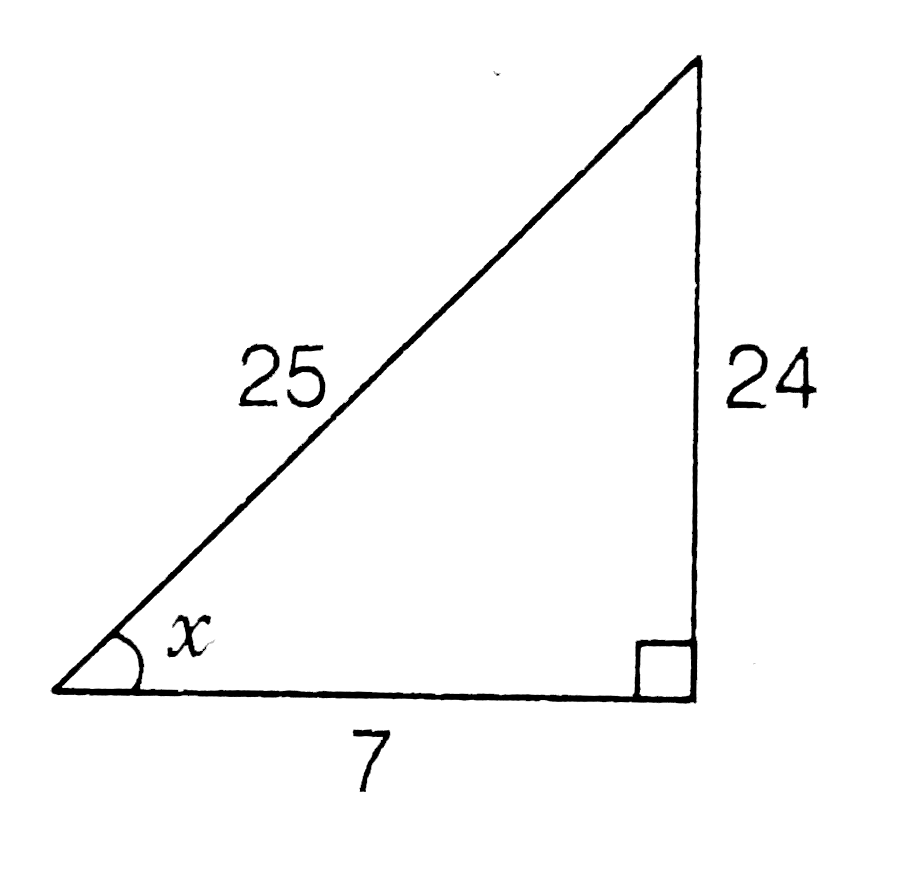
∴cotx=cosxsinx=7252425=724
⇒x=cot−1(724)=cos−1(725)
∴cot(cos−1'725)=cot(cot−1'724)=724,[∵cot−1'724=cos−1'725]
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
The value of cot−1(cot(7π)4) is:
A7π4B−π4Cπ4D3π4The value of tan[sin−1(7/√50)+cos−1(1/√50)+cot−1(1/√7) is equal to
A7B√50C161/73D73/161The value of sin{cot−1[cos(cot−1(1x))]} is equal to (x>0)
A√1+x22+x2B√1−x22+x2C√1+x22−x2D√2+x21+x2
Find the value of 2cos−1.3√13+cot−1.1663+12cos−1.725
View SolutionThe value of cot[sin−1{cos(tan−11)}] is
View SolutionThe value of sin−1(cos2)−cos−1(sin2)+tan−1(cot4)−cot−1(tan4)+sec−1(cosec6)−cosec−1(sec6) is:
View SolutionThe value of sin[cot−1{cos(tan−1x)}] is
View SolutionThe value of cot−17+cot−18+cot−118 is
View Solution
