Let there be n resistors $R_{1} . . . R_{n}$ with $R_{max} = max (R_{1} . . . . R_{n})$ and $R_{min} = min {R_{1} . . . R_{n}}$ . Show that when they are connected in parallel the resultant resistance $R_{p} = R_{min}$ and when they are connected in series, the resultant resistance $R_{S} > R_{max}$ . Interpret the result physically.

Video Solution

Text Solution

Verified by Experts

When all resistances are connected in parallel, the resultant resistance $R_{p}$ is given by
$\frac{1}{R_{p}} = \frac{1}{R_{1}} + . . . . . + \frac{1}{R_{n}}$
On multiplying both sides by $R_{min}$ we have
$\frac{R_{min}}{R_{p}} = \frac{R_{min}}{R_{1}} + \frac{R_{min}}{R_{\circ}} + . . . . + \frac{R_{min}}{R_{n}}$
Here, in RHSlt there exist one term $\frac{R_{min}}{R_{min}} = 1$ and other terms are positive, so we have
$\frac{R_{min}}{R_{p}} = \frac{R_{min}}{R_{1}} + \frac{R_{min}}{R_{2}} + . . . . + \frac{R_{min}}{R_{n}} > 1$
This shows that the resultant resistance $R_{p} < R_{min}$
thus, in parallel combination, the equivalent resistance of resistors is less than the minimum resistance available in combination of resistors. Now, in series combination, the equivalent resistance is given by
$R_{S} = R_{1} + . . . + R_{n}$
Here, in RHS, there exist one term having resistance $R_{max}$
So, we have
or $R_{S} = R_{1} + . . . + R_{max} + . . . + . . . + R_{n}$
$R_{S} = R_{1} + . . . + R_{max} . . . + R_{n} = R_{max} + . . . (R_{1} + . . . +) R_{n}$
or $R_{S} \geq R_{max}$
or $R_{S} = R_{max} (R_{1} + . . . + R_{n})$
Thus, in series combination, the equivalent resistance of resistors of resistors is greater than the maximum resistance available in combination resistors. Physical interpretation.
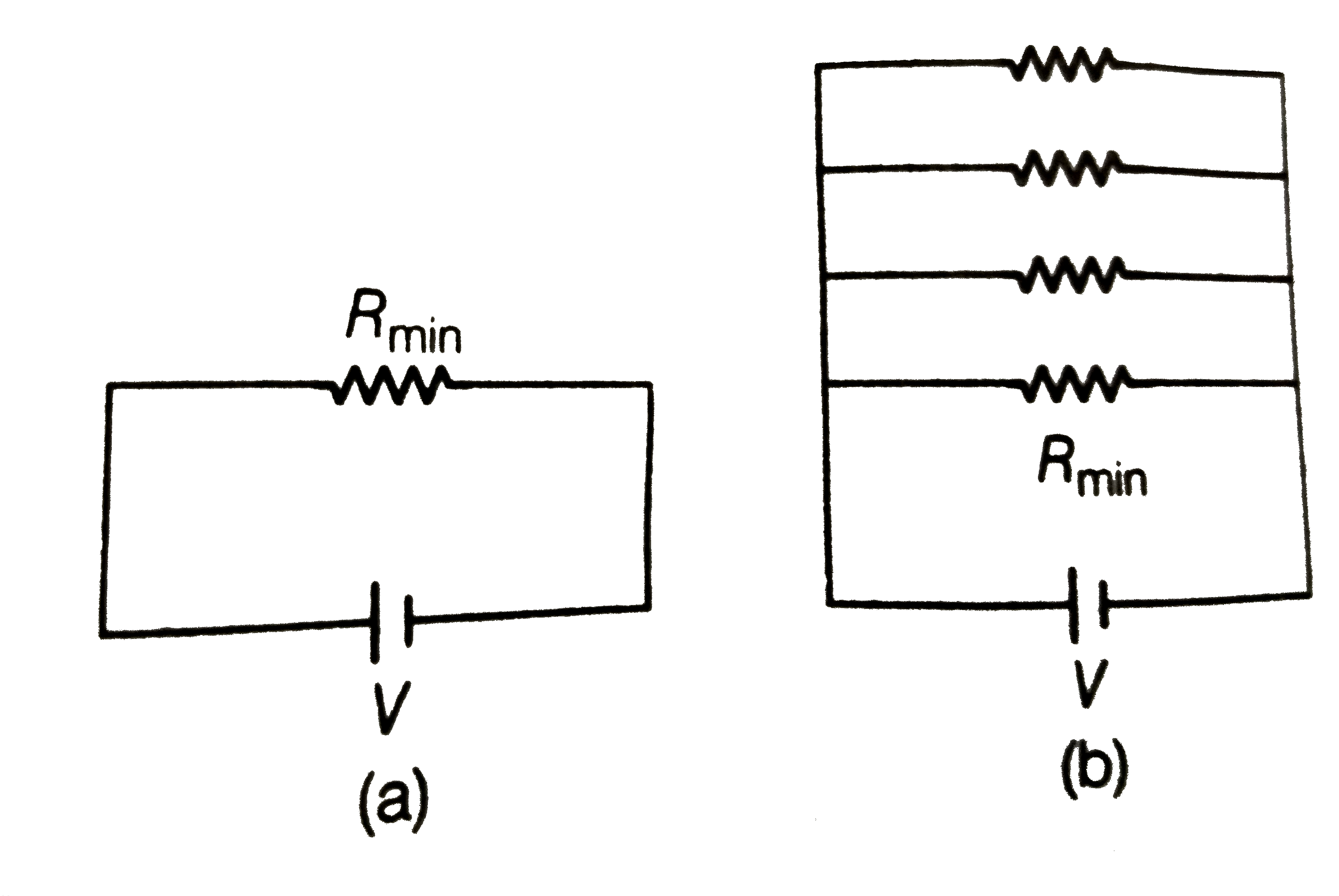
In Fig (b), $R_{min}$ provides an equivalent route as in Fig. (a) for current. But in addition there are (n-1) routes by the remaining (n-1) resistors. Current in fig. (b) is greater than current in Fig. (a). Effective resistance in Fig (b) $< R_{min}$ Second circuit evidently affords a greater resistance.
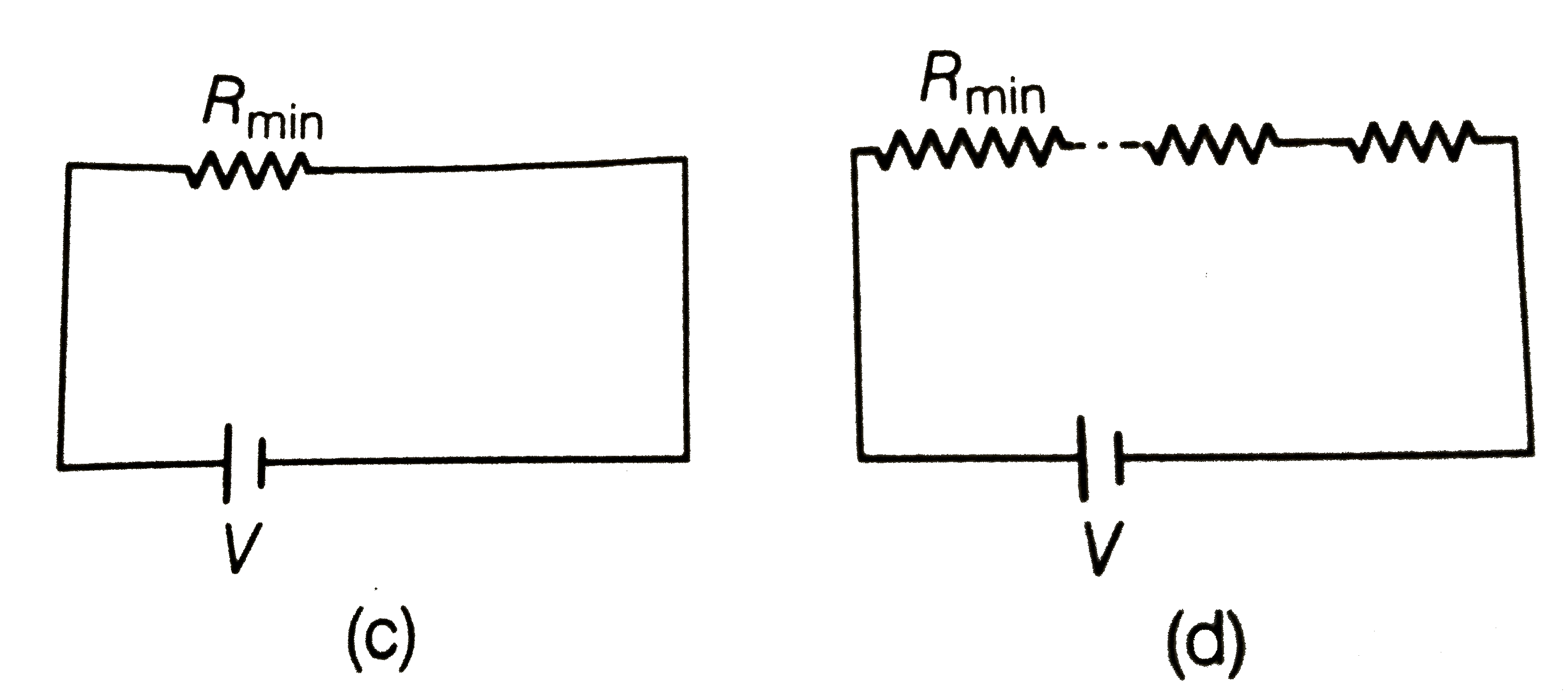
In figure. (d), $R_{max}$ provides an equivalent route as in fig. (c) for current. Current in figure. $(d) <$ current in figure (c) Effective resistance in fig. (b) $< R_{max}$ second circuit evidently affords a greater resistance.

.

Updated on:21/07/2023

Two resistors of resistance $R_{1}$ and $R_{2}$ having $R_{1} > R_{2}$ are connected in parallel. For equivalent resistance R, the correct statement is
A $R > R_{1} + R_{2}$
B $R_{1} < R < R_{2}$
C $R_{2} < R < (R_{1} + R_{2})$
D $R < R_{1}$
There are n similar conductors each of resistance R . The resultant resistance comes out to be x when connected in parallel. If they are connected in series, the resistance comes out to be
A $x / n^{2}$
B $n^{2} x$
C $x / n$
Dnx
Two resistors of resistances $R_{1} = (300 \pm 3) Ω$ and $R_{2} = (500 \pm 4) Ω$ are connected in series. The equivalent resistance of the series combination is
A $(800 \pm 1) Ω$
B $(800 \pm 7) Ω$
C $(200 \pm 7) Ω$
D $(200 \pm 1) Ω$