A rectangular conducting loop consists of two wires on two opposite sides of length l joined together by rods of length d. The wires are each of the same material but with cross-sections differing by a factor of 2. The thicker wire has a resistance R and the rods are of low resistance, which in turn are connected to a constant voltage source $V_{0}$ . The loop is placed in a uniform magnetic field B at $45^{\circ}$ to its plane. Find $τ$ , the torque exerted by the magnetic field on the loop about an axis through the centres of rods.

Video Solution

Text Solution

Verified by Experts

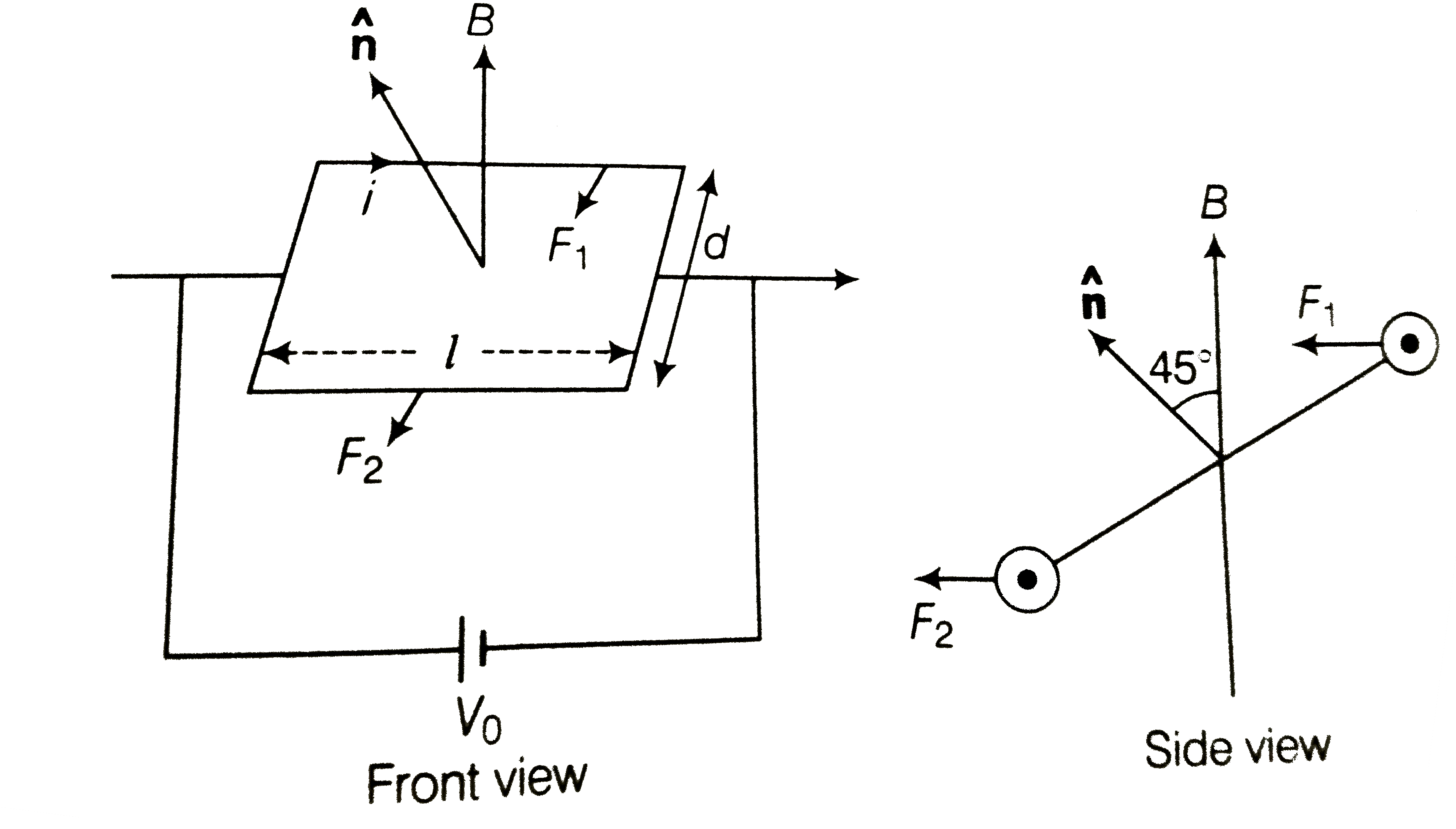
Thicker wire has a resistance R, then the other wire has a resistance 2R as the wires are of the same material but with cross-sections differing by a factor 2.
Now, the force and hence, torque on first wire is given by
$F_{1} = i_{1} i B = \frac{V_{0}}{2 R} l B, τ_{1} = \frac{d}{2 \sqrt{2}} F_{1} = \frac{V_{0} l d B}{2 \sqrt{2} R}$
Similarly, the force hence torque on otehr wire is given by
$F_{2} = i_{2} l B = \frac{V_{0}}{2 R} l B, τ_{2} = \frac{d}{2 \sqrt{2}} F_{2} = \frac{V_{0} l d B}{4 \sqrt{2} R}$
So, net torque $τ = τ_{1} - τ_{2}$
$τ = \frac{1}{4 \sqrt{2}} \frac{V_{0} l d B}{R}$

|

Updated on:21/07/2023

Class 12 PHYSICS MOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A rectangular conducting loop consists of two wires on two opposite sides of length l joined together by rods of length d. The wires are each of the same material but with cross-sections differing by a factor of 2. The thicker wire has a resistance R and the rods are of low resistance, which in turn are connected to a constant voltage source $V_{0}$ . The loop is placed in a uniform magnetic field B at $45^{\circ}$ to its plane. Find $τ$ , the torque exerted by the magnetic field on the loop about an axis through the centres of rods.
A $\frac{V_{0} A B}{4 \sqrt{2} R}$
B $\frac{V_{0} A B}{\sqrt{2} R}$
C $\frac{V_{0} A B}{2 \sqrt{2} R}$
D $\frac{3 V_{0} A B}{\sqrt{2} R}$
Question 2 - Select One
Two wire of the same meta have same length, but their cross-sections are in the rati $3 : 1$ . They are joined in series. The resistance of thicker wire is $10 Ω$ . The total resistance of the combination will be
A $10 Ω$
B $20 Ω$
C $40 Ω$
D $100 Ω$
Question 3 - Select One
Two wires of the same metal have same length, but their cross-sections are in the ratio 3:1 . They are joined in series. The resistance of thicker wire is $10 Ω$ . The total resistance of the combination will be
A $2.5 Ω$
B $40 / 3 Ω$
C $40 Ω$
D $100 Ω$

NCERT EXEMPLAR-MOVING CHARNGES AND MAGNETISM-Moving Charnges And Magnetism

Home
Ask Doubt
Profile