A uniform conducting wire of length 12a and resistance R is wound up as a current carrying coil in the shape of (i) an equilateral triangle of side a, (ii) a square of sides a and, (iii) a regular hexagon of sides a. The coil is connected to a voltage source V0. Find the magnetic moment of the coils in each case.


We know that magnetic moment of the coils m=nlA.
Since, the same wire is used in three cases with same potential, therefore, same current flows in three cases.
(i) for an equilateral triangle of side a,
n=4 as the total wire of length =12a
Magnetic moment of the coils m=nIA=4I(√33a2)
∴m=Ia2√3.
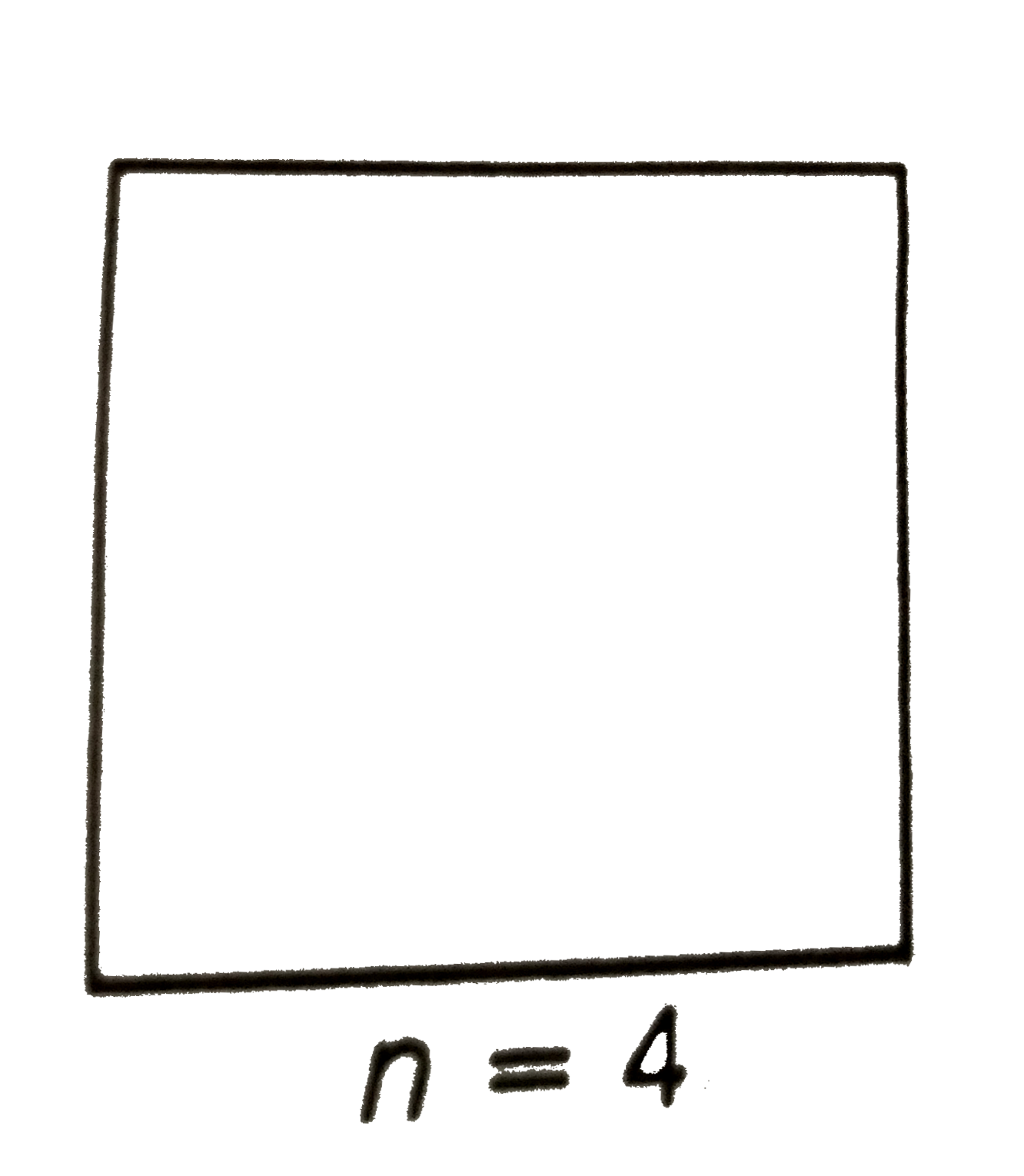
(ii). For a square of sides a,
n=3 as the total wire of length=12a
Magnetic moemnt of the coils m=nIA=3I(a2)=3Ia2
(iii). For a regular hexagon of sides a,
n=2 as the total wire of length =12a
Magnetic moment of the coils m=nlA=21(6√34a2)
m=3√3a2I
m is a geometric series.
Topper's Solved these Questions
Similar Questions
A uniform conducting wire of length 12a and resistance 'R' is wound up as a current carrying coil in the shape of
1. an equilateral triangle of side 'a'
2. a square of side 'a'
The magnetic dipole moments of the coil in each case resp. are.
View SolutionA uniform conducting wire of length 18a and resistance R is wound up as current carrying coil in the shape of a regular a hexagon of sides a. If the coil is connected to a voltage source V0, then the magnetic moment of coil is

View Solution
Knowledge Check
A regular hexagone of side a. A wire of length 24 a is coiled on that hexagone. If current in hexagone is I, then find the magnetic moment.
 A6√3la2B3√3la2C3√32la2D6la2
A6√3la2B3√3la2C3√32la2D6la2A current I is flowing in a hexgonal coil of side a figure. The magnetic field induction at the centre O of the coil will be
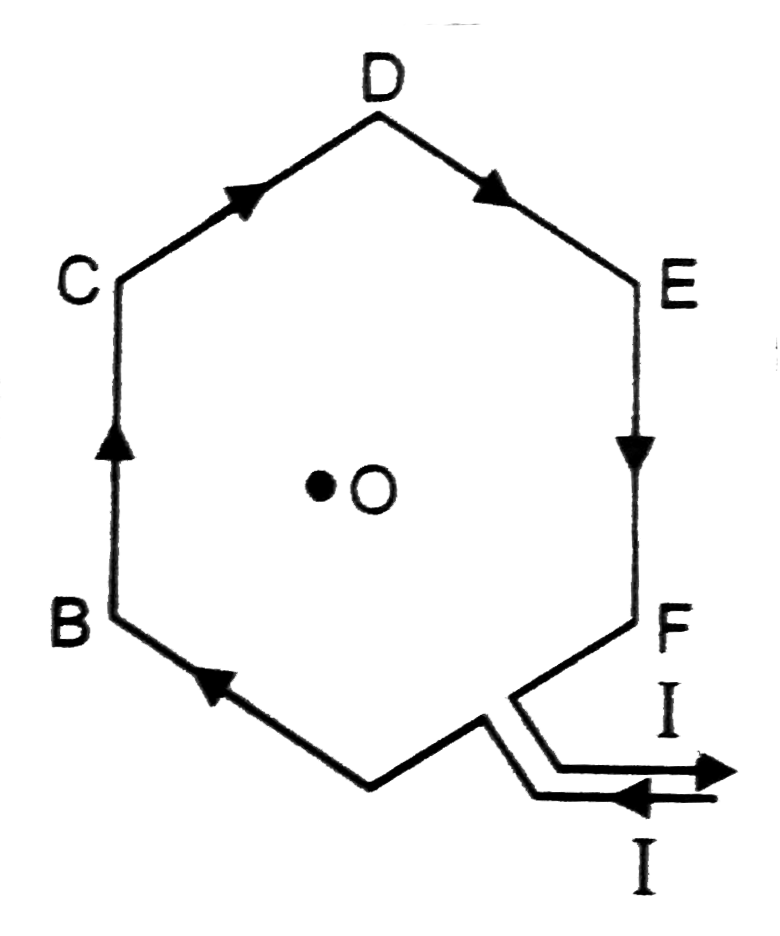 A√2μ0IπaB√3μ0IπaC2πa√3IDμ0Iπa
A√2μ0IπaB√3μ0IπaC2πa√3IDμ0Iπa
A uniform conducting wire of length length 10a and resistance R is wound up into four turn as a current carrying coil in the shape of equilateral triangle of side a. If current I is flowing 4 through the coil then the magnetic moment of the coil is
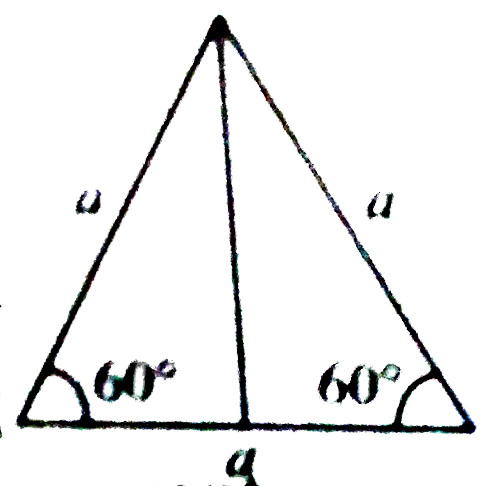
View SolutionA square loop of side l carries a current i. it is placed as shown in figure. Find the magnetic moment of the loop.
View SolutionA wire shaped to a regular hexagon of side 2cm carries a current of 2A. Find the magnetic field at the cetre of the hexagon.
View SolutionA loop in the shape of an equilateral triangle triangle of side a carries a current I as shown in the figure.Find out the magnetic field at the centre C of the triangle.

View SolutionA square loop OABCO of side of side l carries a current i. It is placed as shown in figure. Find the magnetic moment of loop.

View SolutionAn equilateral triangle of side length l is formed from a piece of wire of uniform resistance. The current I is as shown in figure. Find the magnitude of the magnetic field at its centre O.

View Solution
