Consider a circular current-carrying loop of radius R in the x-y plane with centre at origin. Consider the line integral $ζ (L) = ∣ ∣ ∣ \int_{- L}^{L} \to B . d \to l ∣ ∣ ∣$ taken along z-axis.
(a) Show that $ζ (L)$ monotonically increases with L.
(b) Use an appropriate Amperian loop to show that $ζ (\infty) = μ_{0} I$ , where I is the current in the wire.
(c) Verify directly the above result.
(d) Suppose we replace the circular coil by a square coil of sides R carrying the same current I. What can you say about $ζ (L)$ and $ζ (\infty)$ ?

Video Solution

Text Solution

Verified by Experts

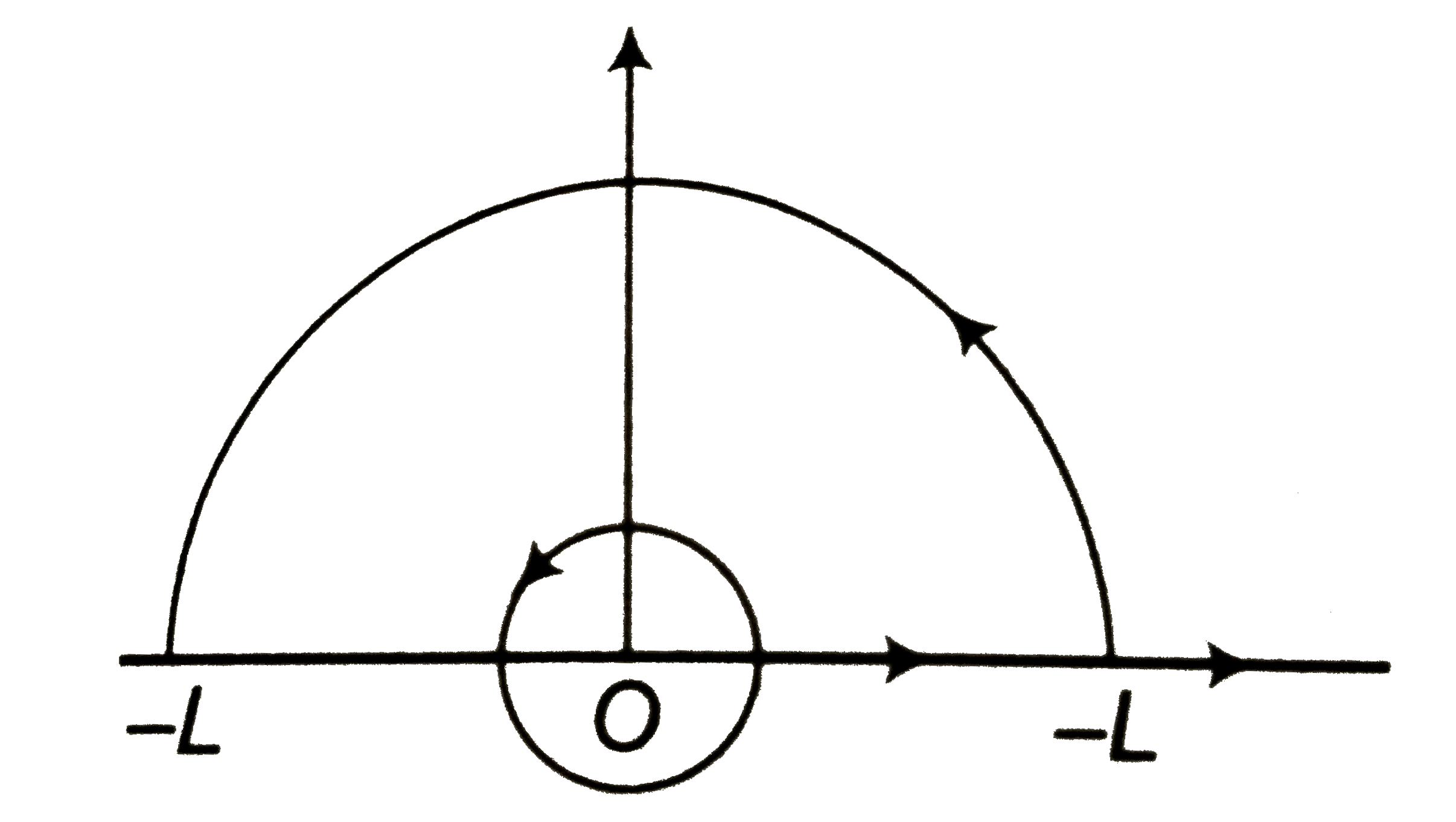
(a). B(z) points in the same direction on z-axis and hence , J(L) is a monotonically function of L. ltbtgt Since B and dl along the same direction, therefore B.dl=B.dl as cos0=1
(b). J(L)+contribution from large distance on contour $C = μ_{0} I$ $∴$ as $L \to \infty$
Contribution form large distance $\to 0$ (as $B \propto 1 / r^{3}$ )
$J (\infty) - μ_{0} I$
(c). the magnetic field due to circular current-carrying loop of radius R in the x-y plane with centre at origin at any point lying at a distance of from origin.
$B_{Z} = \frac{μ_{0} l R^{2}}{2 {(Z^{2} + R^{2})}^{3 / 2}}$
$\int_{- \infty}^{\infty} B_{Z} d z = \int_{- \infty}^{\infty} \frac{μ_{0} l R^{2}}{2 {(Z^{2} + R^{2})}^{3 / 2}} d z$
Put $Z = R {tan θ}_{1}$
$\Rightarrow d Z = R {sec}^{2} θ d θ$
$∴ \int_{- \infty}^{\infty} B_{z} d z = \frac{μ_{0} I}{2} \int_{- π / 2}^{π / 2} cos θ d θ = μ_{0} I$
(d). $B {(Z)}_{square} < B {(Z)}_{circular coil}$
$\sum {(L)}_{square} < \sum {(L)}_{circular coil}$
but by using arguments as in (b)
$\sum {(\infty)}_{square} = s u n {(\infty)}_{circular}$

Updated on:21/07/2023

The magnetic field at centre of a hexagonal coil of side l carrying a current I is

A $\frac{\sqrt{3} μ_{0} I}{π l}$
B $\frac{μ_{0} I}{4 π l}$
C $\frac{π μ_{0} I}{\sqrt{3} l}$
Dzero
A current carrying circular loop of radius R is placed in the x-y plane with centre at the origin. Half of the loop with $x > 0$ is now bent so that it now lies in the y-z plane.
AThe magnitude of magnetic moment now diminishes
BThe magnetic moment does not change
CThe magnitude of $\to B$ at $(0, 0, z), z > > R$ increases
DThe magnitude of $\to B$ at $(0, 0, z), z > > R$ is unchanged
The magnetic field at the point of intersection of diagonals of a square wire loop of side L, carrying a current I is
A $\frac{μ_{0} I}{π L}$
B $\frac{2 μ_{0} I}{π L}$
C $\frac{\sqrt{2} μ_{0} I}{π L}$
D $\frac{2 \sqrt{2} μ_{0} I}{π L}$