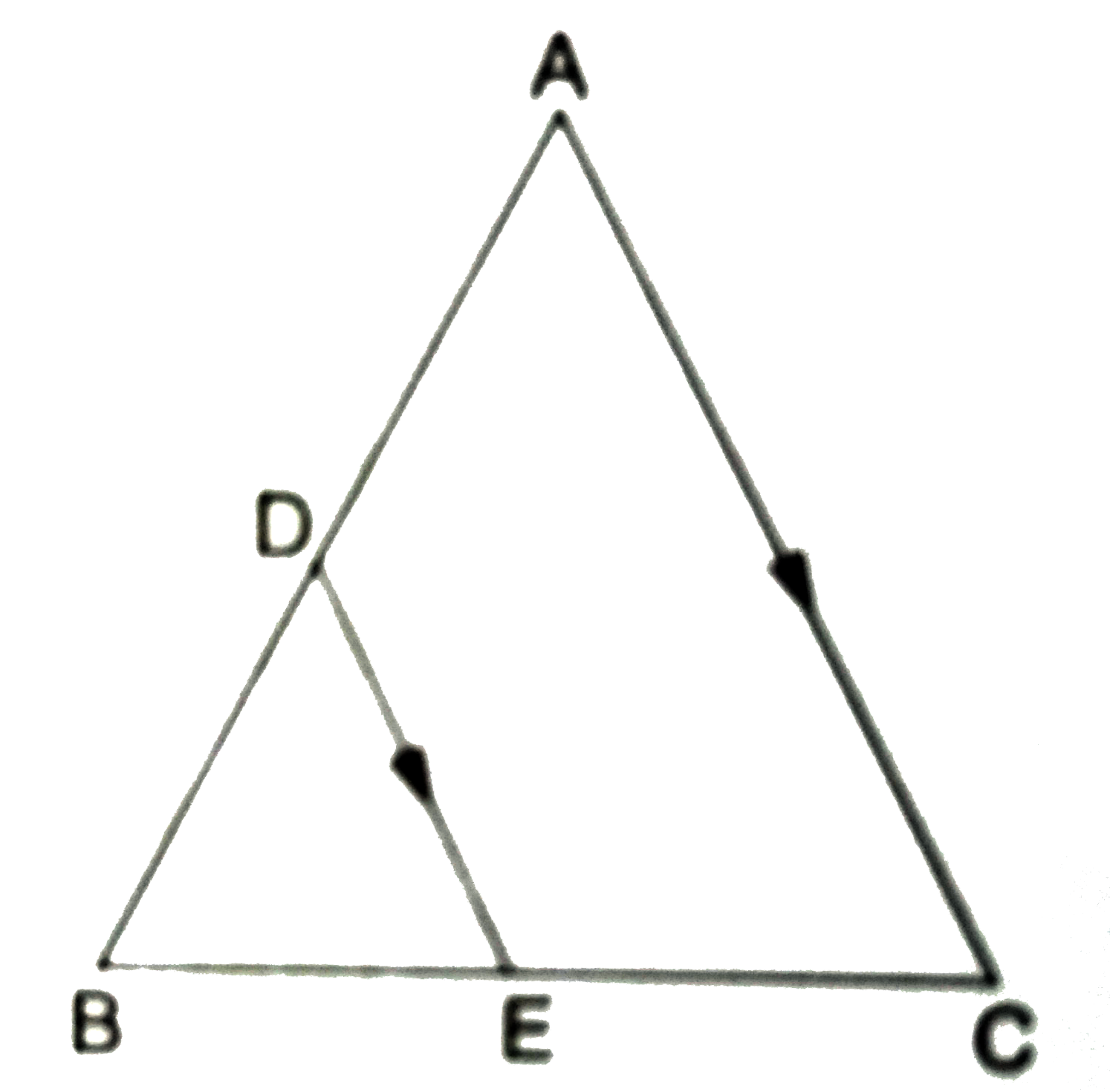
If D is a Point on the side BC of a ΔABC such that AD bisects ∠BAC. Then
A
BD=CD
B
BA>BD
C
BD>BA
D
CD<CA
Video Solution
Text Solution
The correct Answer is:B
Given,ΔABCsuch that AD bisects ∠BAC
∵∠BAD=∠CAD
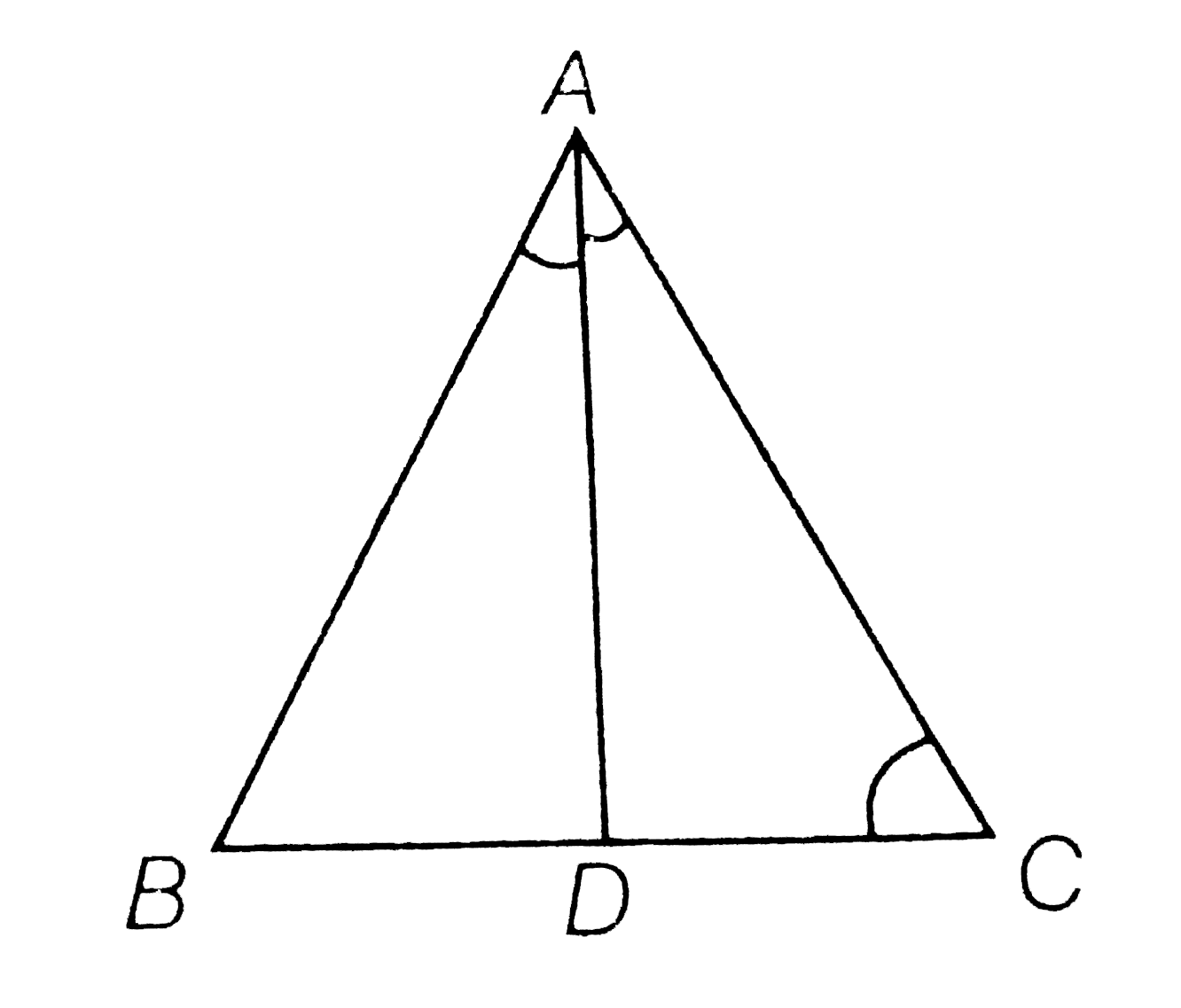
InΔACD,∠BDAis an exterior angle.
∴∠BDA>∠CAD
[∵exterior angle>interior opposite angle]
⇒∠BDA>an≥lBAD [from Eq.(i)]
⇒BA>BD [side opposite to greater angle is greater]
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
D is a point on the side BC of a ΔABC such that AD bisects ∠BAC . Then
ABD=CDBBA>BDCBD>BADCD>CAD is a point on side BC of a Triangle ABC such that AD⊥BC and E is a point on AD for which AeED=51 If ∠BAD=30∘tan∠ACB=6tan∠DBE . find ∠ACB
A30∘B45∘C60∘D15∘Let O be the in-centre of a triangle ABC and D be a point on the side BC of ΔABC, such that OD⊥BC If ∠BOD=15∘, then ∠ABC=?
A75∘B45∘C150∘D90∘
Let O be the in-centre of a triangle ABC and D be a point on the side BC of ΔABC, such that OD⊥BC If ∠BOD=15∘, then ∠ABC=?
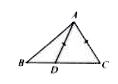
View SolutionD is a point on side BC of ΔABCsuch that AD = AC(see Fig. 7.47).Show that AB > AD.
View SolutionIf D is a point of the base BC of an isosceles triangle ABC such that AD is perpendicular to AC, then a=
View SolutionIn figure ,D and E are Points on side BC of a ΔABC such that BD=CE and AD=AE.Show that ΔABD≅ΔACE.
View SolutionD is a point on side BC of triangle ABC such that AD = AC (see figure). Show that AB>AD.
View Solution