D is a point on side BC of ΔABCsuch that AD = AC(see Fig. 7.47).Show that AB > AD.
∠ADC is a isosceles triangle
∠ADC=∠ACD
In∠ABD
∠ADC=∠ABD+∠BAD
∠ADC>∠ABC
∠ACD>∠ABC
∠ACB>∠ABC
In∠ABC
∠ACB>∠ABC
AB>AC
AB>AD.
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.46videos
TRIANGLES
- BOOK - NCERTCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.18videos
TRIANGLES
- BOOK - NCERTCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.28videos
TRIANGLES
- BOOK - NCERTCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - EXERCISE 13.810videos
SURFACE AREAS AND VOLUMES
Similar Questions
D is a point on side BC of ΔABCsuch that AD = AC(see Fig. 7.47).Show that AB > AD.
View SolutionIn figure D is a point on side BC of a ΔABCsuch that BDCD=ABAC. Prove that AD is the bisector of ∠BAC.
 View Solution
View SolutionE and F are respectively the mid-points of equal sides AB and AC of ΔABC(see Fig. 7.28). Show that BF = C E.
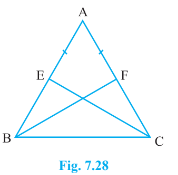 View Solution
View SolutionΔABC is an isosceles triangle in which AB=AC. Side BA is produced to D such that AD=AB (see Fig. 7.34). Show that ∠BCD is a right angle.
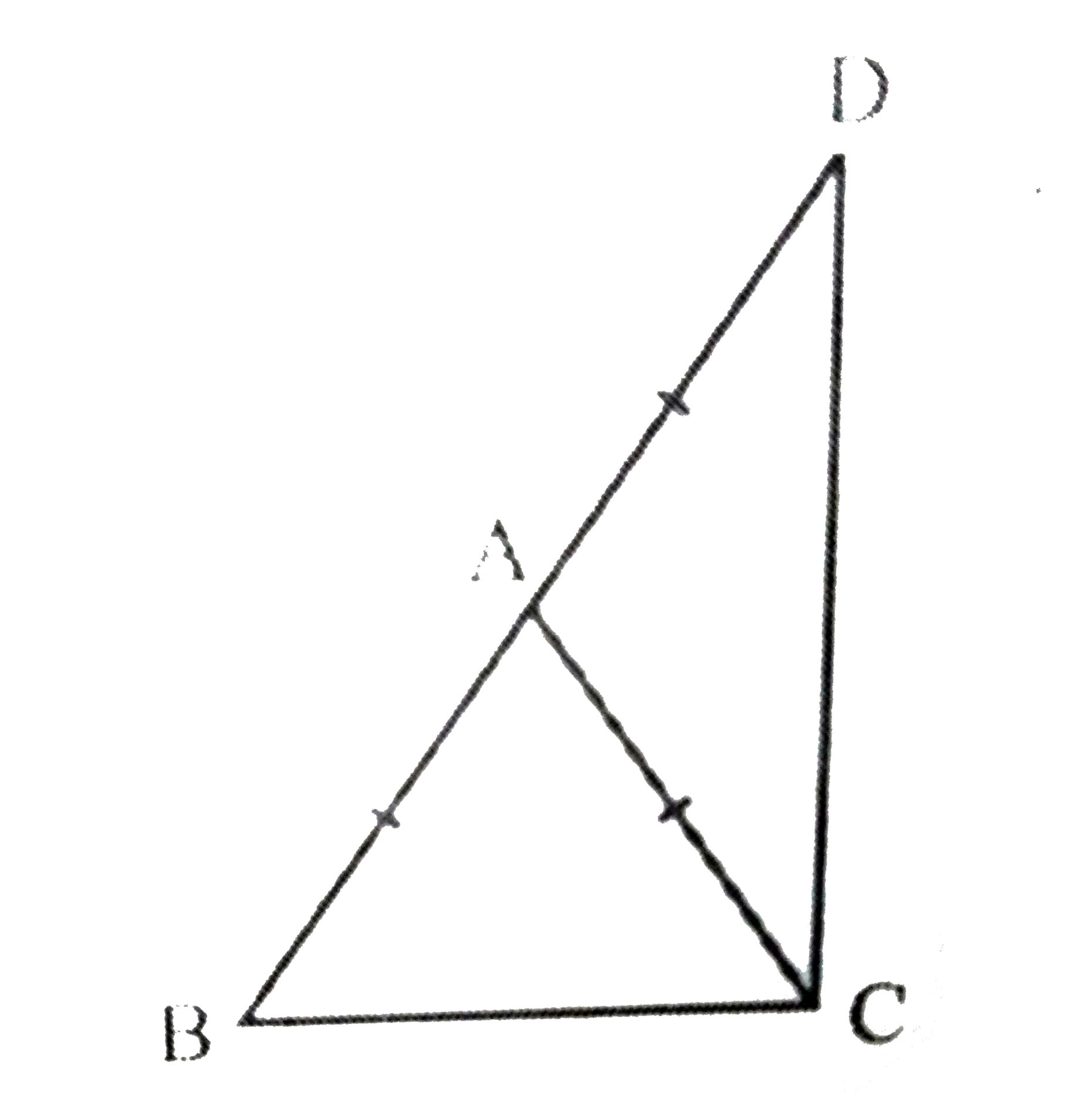 View Solution
View SolutionIn an isosceles triangle ABC with AB=AC, D and E are points on BCsuch that BE=CD(see Fig. 7.29). Show that AD=AE
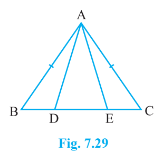 View Solution
View SolutionA point D is taken on the side BC of a ABC such that BD=2dC. Prove that ar(ABD)=2ar(ADC).
View SolutionA point D is taken on the side BC of a ABC such that BD=2DC. Prove that ar ( ABD)= 2 ar ( ADC)
View SolutionTwo sides AB and BC and median AM of one triangle ABC are respectively equal to side PQ and QR and median PN of ΔABC≅ΔPQR(see Fig. 7.40). Show that:
(i) ΔABM≅ΔPQN
(ii) ΔABC≅ΔPQR
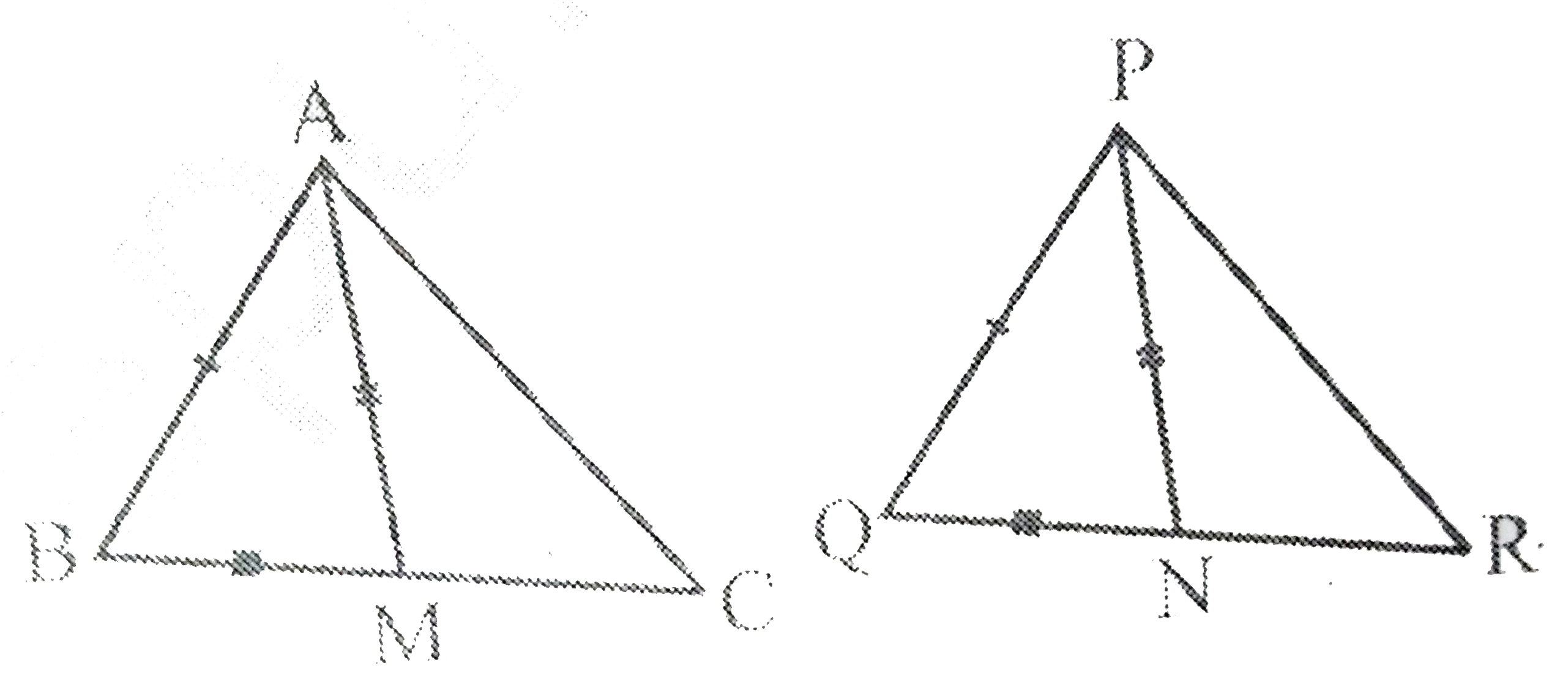 View Solution
View SolutionD and E are points on sides AB and AC respectively of ΔABCsuch thatar (DBC) = ar (EBC). Prove that DE ∣∣ BC.
View SolutionIn fig.9, D is a point on side BC of a ABC. AD is joined. Name all the triangle that you can observe in the figure. How many are they?
View Solution

