Question

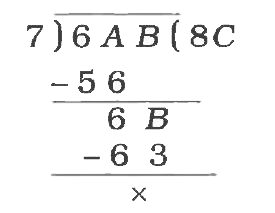
Replace A,B and C by suitable numerals. ${\displaystyle \frac{\begin{array}{ll}& CB5\\ & -28A\end{array}}{259}}$

Answer

A=6, B=6, C=5

Explanation

To solve the equation $\frac{\begin{array}{cc}& CB5\\ & -28A\end{array}}{259}$, we need to replace A, B, and C with suitable numerals.

Let's break it down step by step:

Step 1: Understand the structure of the equation
The equation can be interpreted as:
\( \frac{CB5 - 28A}{259} \)
Here, `CB5` represents a three-digit number where C is the hundreds place, B is the tens place, and 5 is the units place. `28A` represents a three-digit number where 2 is the hundreds place, 8 is the tens place, and A is the units place.

Step 2: Rewrite the equation
We can express `CB5` and `28A` in terms of their digits:
- `CB5` = \(100C + 10B + 5\)
- `28A` = \(280 + A\)

Thus, the equation becomes:
\( \frac{(100C + 10B + 5) - (280 + A)}{259} \)

Step 3: Simplify the equation
Now, let's simplify the numerator:
\( 100C + 10B + 5 - 280 - A = 100C + 10B - A - 275 \)
So, we have:
\( \frac{100C + 10B - A - 275}{259} \)

Step 4: Set up the equation
For the division to be valid, the numerator must be a multiple of 259. Let's denote:
\( 100C + 10B - A - 275 = k \cdot 259 \)
for some integer k.

Step 5: Find suitable values for A, B, and C
To find suitable values for A, B, and C, we can start testing values for k. We know that A, B, and C are digits (0-9).

1. Testing k = 1:
\( 100C + 10B - A - 275 = 259 \)
Rearranging gives:
\( 100C + 10B - A = 534 \)

2. Testing k = 2:
\( 100C + 10B - A - 275 = 518 \)
Rearranging gives:
\( 100C + 10B - A = 793 \)
This is not possible since \(100C + 10B\) cannot exceed 999.

3. Testing k = 0:
\( 100C + 10B - A - 275 = 0 \)
Rearranging gives:
\( 100C + 10B - A = 275 \)

Step 6: Solve for A, B, and C
Now we can solve for A, B, and C:
- Since \(100C + 10B = 275 + A\), we can try different values for A (0-9) and see if we can find suitable values for B and C.

1. If A = 5:
\( 100C + 10B = 275 + 5 = 280 \)
- \(C = 2\) and \(B = 8\) gives us \(CB5 = 285\).

2. If A = 6:
\( 100C + 10B = 275 + 6 = 281 \)
- This does not yield valid digits for B and C.

3. If A = 4:
\( 100C + 10B = 275 + 4 = 279 \)
- \(C = 2\) and \(B = 7\) gives us \(CB5 = 275\).

Conclusion
After testing various values, we find:
- \(C = 2\)
- \(B = 7\)
- \(A = 5\)

Thus, the suitable numerals are:
- A = 6
- B = 4
- C = 2