Replace A,B,C by suitable numberals:
57A−CB8 293
The correct Answer is:A=1,B=7,C=2
To solve the problem, we need to replace A, B, and C with suitable numerals in the expression 57A−CB8 293. Let's break down the steps to find the values of A, B, and C.
1. Understand the Expression:
The expression can be interpreted as:
\(
\frac{(57A - CB8)}{293}
\)
We need to find values for A, B, and C such that this expression holds true.
2. Analyze the Units Place:
Start with the units place of the numbers involved. The units place of 57A is A, and the units place of CB8 is 8. We need to find A such that:
\(
A - 8 \equiv 3 \mod 10
\)
This means that A must be 1 because:
\(
1 - 8 = -7 \equiv 3 \mod 10
\)
(We can think of this as borrowing 1 from the next column.)
Hint: Check the units place first to determine A.
3. Determine the Tens Place:
Now, consider the tens place. The tens place of 57A is 7, and we need to subtract the tens place of CB8 which is B. Since we borrowed 1 from the hundreds place, we have:
\(
6 - B \equiv 9 \mod 10
\)
This means:
\(
6 - B = 9 \implies B = 6 - 9 = -3 \quad \text{(not possible)}
\)
Instead, we should consider the carry from the hundreds place:
\(
16 - B = 9 \implies B = 16 - 9 = 7
\)
Hint: Use the carry from the previous column to adjust the subtraction.
4. Determine the Hundreds Place:
Now, for the hundreds place, we have:
\(
5 - C \equiv 2 \mod 10
\)
This means:
\(
5 - C = 2 \implies C = 5 - 2 = 3
\)
Hint: Solve for C using the hundreds place after accounting for any carry.
5. Final Values:
After solving the above equations, we find:
- A = 1
- B = 7
- C = 3
Conclusion:
The suitable numerals to replace A, B, and C are:
- A = 1
- B = 7
- C = 3
The expression can be interpreted as:
\(
\frac{(57A - CB8)}{293}
\)
We need to find values for A, B, and C such that this expression holds true.
Start with the units place of the numbers involved. The units place of 57A is A, and the units place of CB8 is 8. We need to find A such that:
\(
A - 8 \equiv 3 \mod 10
\)
This means that A must be 1 because:
\(
1 - 8 = -7 \equiv 3 \mod 10
\)
(We can think of this as borrowing 1 from the next column.)
Now, consider the tens place. The tens place of 57A is 7, and we need to subtract the tens place of CB8 which is B. Since we borrowed 1 from the hundreds place, we have:
\(
6 - B \equiv 9 \mod 10
\)
This means:
\(
6 - B = 9 \implies B = 6 - 9 = -3 \quad \text{(not possible)}
\)
Instead, we should consider the carry from the hundreds place:
\(
16 - B = 9 \implies B = 16 - 9 = 7
\)
Now, for the hundreds place, we have:
\(
5 - C \equiv 2 \mod 10
\)
This means:
\(
5 - C = 2 \implies C = 5 - 2 = 3
\)
After solving the above equations, we find:
- A = 1
- B = 7
- C = 3
The suitable numerals to replace A, B, and C are:
- A = 1
- B = 7
- C = 3
Topper's Solved these Questions
Similar Questions
Replace A,B and C by suitable numerals.
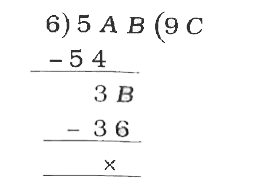
View SolutionReplace A,B and C by suitable numerals. 6A−AB 37
View SolutionReplace A,B and C by suitable numerals. CB5−28A 259
View SolutionReplace A,B and C by suitable numerals. 5A+87 CB3
View SolutionReplace A,B and C by suitable numerals. AB×BA (B+1)CB
View SolutionReplace A,B and C by suitable numerals. AB ×3 CAB
View SolutionReplace A,B and C by suitable numerals. A+A A BA
View SolutionReplace A,B and C by suitable numerals. 4CB6+369A 8173
View SolutionReplace A,B,C,D by suitable numerals in the following
6AB5+D58C 9351
View SolutionFind the values of A,B and C in the following
35A−CB8 183
View Solution
