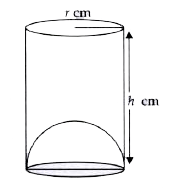
The capacity of a cylinder vessel with a hemisphere portion raised upward at the bottom as shown in the figure is πr23[3h−2r]
![The capacity of a cylinder vessel with a hemisphere portion raised upward at the bottom as shown in the figure is (pir^(2))/(3) [3h - 2r]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/ARH_NCERT_EXE_MATH_X_C12_S01_026_S01.png)
True
We know that, capacity of cylinderical vessel =πr2hcm3
and capacity of hemisphere =23πr3cm
From the figure, capacity of the cylindrical vessel
=πr2h−23πr3=13πr2[3h−2r]
Topper's Solved these Questions
Similar Questions
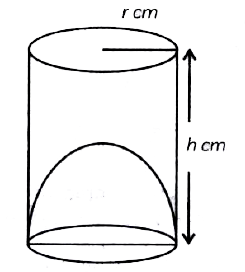
The capacity of a cylindrical vessel with a hemispherical portion raised upward, at the bottom as shown in the given is πr23(3h−2r).
View SolutionThe capacity of a cylindrical vessesl with a hemispherical portion raised upwards at the bottom as shown in the given figure is πr23[3h−2r].
View Solution
Knowledge Check
- Question 1 - Select One
A hemispherical cavity of radius R is created in a solid sphere of radius 2R as shown in the figure . Then y -coordinate of the centre of mass of the remaining sphere is
AYCM=−R15BYCM=−R40CYCM=−R30DYCM=−R20
Consider a cuboidal vessel (2R×2R×R) with as hemispherical cavity of radius R, kept at a horizontal smooth surface as shown in the figure. The vessel has very small hole of cross-sectional area "a". Now water of density ρ is poured into space developed due horizontal surface adn vessel through hole very slowly. When the height of waer level is h, the vessel lifts off the surface and liquid leaks through space generated. (R=2m,ρ=103kg/m3,m=9πkg). If the value of h is 5kcm, find the value of k.
(Atmospheric pressure =105N/m2).
View SolutionA wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in the figure. If the height of the cylinder is 10 cm and its base of radius 3.5 cm. Find the total surface area of the article.
View SolutionIn the circuit shown in figure , R1=R2=R3=R. Match the following
View SolutionIf the radius of the base and height of a cylinder and cone are each equal to r , and the radius of a hemisphere is also equal to r , then the volumes of the cone, cylinder and hemisphere are in the ratio (a) 1 : 2 : 3 (b) 1 : 3 : 2 (c) 2 : 1 : 3 (d) 3 : 2 : 1
View SolutionA water tank open at the top is hemispherical at the bottom and cylindrical above it. If radius of the hemisphere is 12 m and the total capacity of the tank is 3312π m3 , then the ratio of the surface areas of the hemispherical and the cylindrical portions is (a) 1 : 1 (b) 3 : 5 (c) 4 : 5 (d) 6 : 5
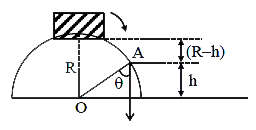
View SolutionA small block slides down from the top of hemisphere of radius R = 3 m as shown in the figure. The height 'h' at which the block will lose contact with the surface of the sphere is __________ m.
(Assume there is no friction between the block and the hemisphere)
View SolutionThe height h of cylinder equals the circumference of the cylinder. In terms of h, what is the volume of the cylinder? h34π (b) h22π (c) h32 (d) πh3
View Solution